计算机视觉(本科) 北京邮电大学 鲁鹏 第二次作业 词袋模型图片分类
https://github.com/woriazzc/beiyouCV/tree/master/02
任务
编写一个图像分类系统,能够对输入图像进行类别预测。具体的说,利用数据库的2250张训练样本进行训练;对测试集中的2235张样本进行预测。
数据库说明:scene_categories数据集包含15个类别(文件夹名就是类别名),每个类中编号前150号的样本作为训练样本,15个类一共2250张训练样本;剩下的样本构成测试集合。
数据集详情可参阅: https://qixianbiao.github.io/Scene.html
数据集下载地址: https://figshare.com/articles/15-Scene_Image_Dataset/7007177
使用知识点: SIFT特征、Kmeans、词袋表示、支撑向量机
算法流程
- 提取数据集中的样本,并划分训练集和测试集
-----------------------特征提取与词典生成----------------------- - 对于训练集的所有图片,提取图片的SIFT 特征点,并对SIFT 特征点向量归一化
- 对所有SIFT 特征点使用聚类算法分为n 类
- 将n 类特征点的中心点作为视觉词汇,生成词袋(字典)
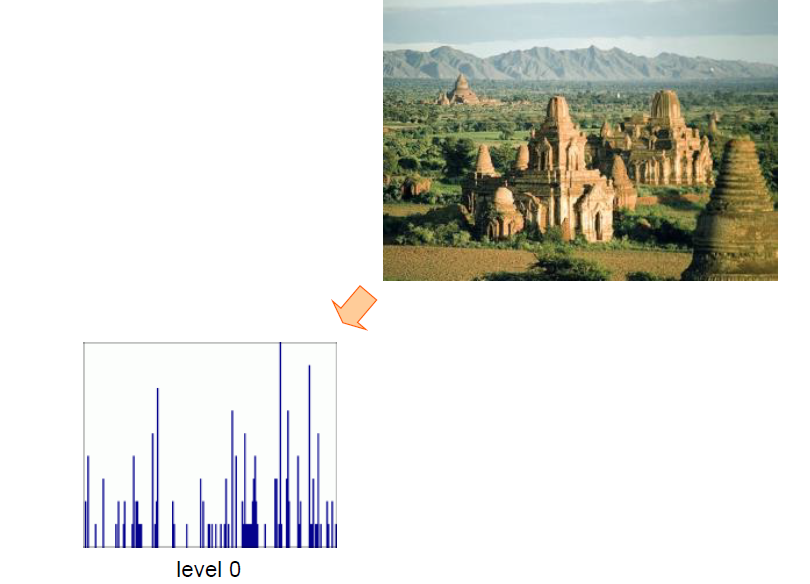
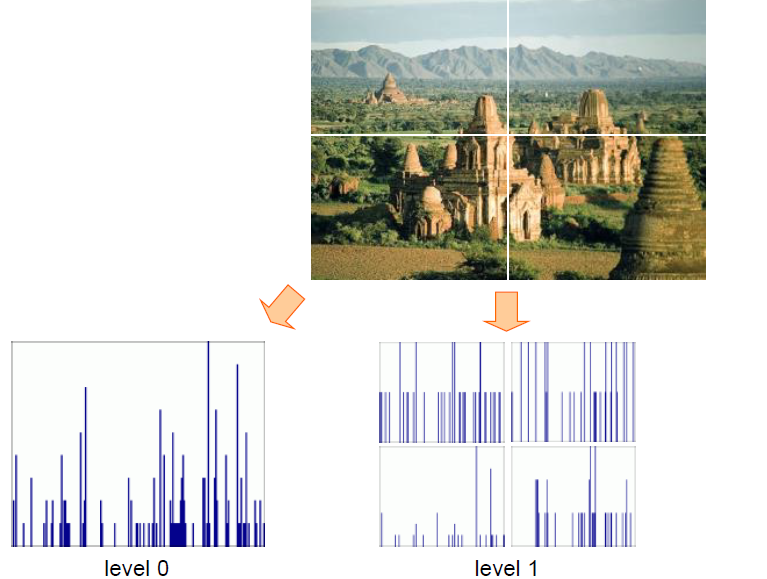
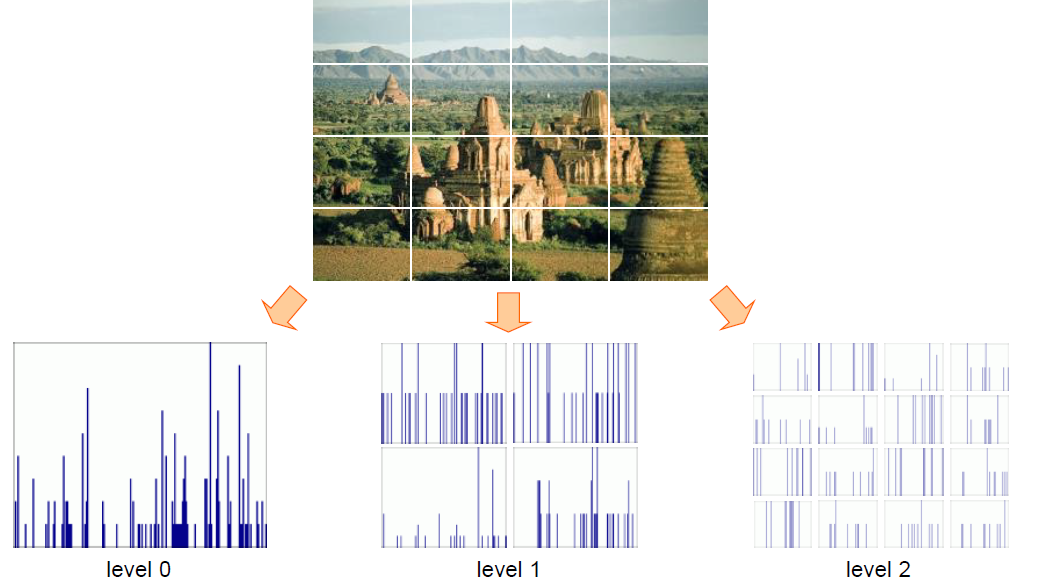
-----------------------图片表示----------------------- - 使用论文中的SPM 算法生成图片的特征向量
a) 将图片分为3 种尺度,分别为11、22、4*4 大小,统计不同尺度下的特征直方图
b) 将不同尺度下的特征直方图合并,组合成为一个21(1 + 4 + 16) * n 维度大小的特征向量
-----------------------执行分类----------------------- - 将图片的特征向量作为数据集,使用支持向量机算法完成分类任务
- 对测试集图片做和训练集相同的数据处理操作
- 使用支持向量机模型对测试集图片的类别进行预测
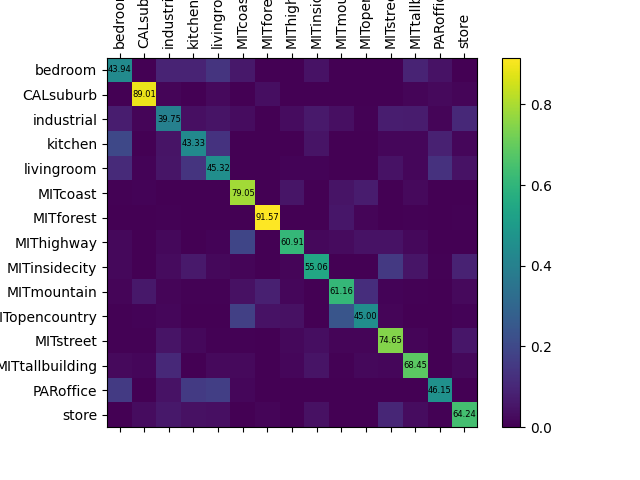
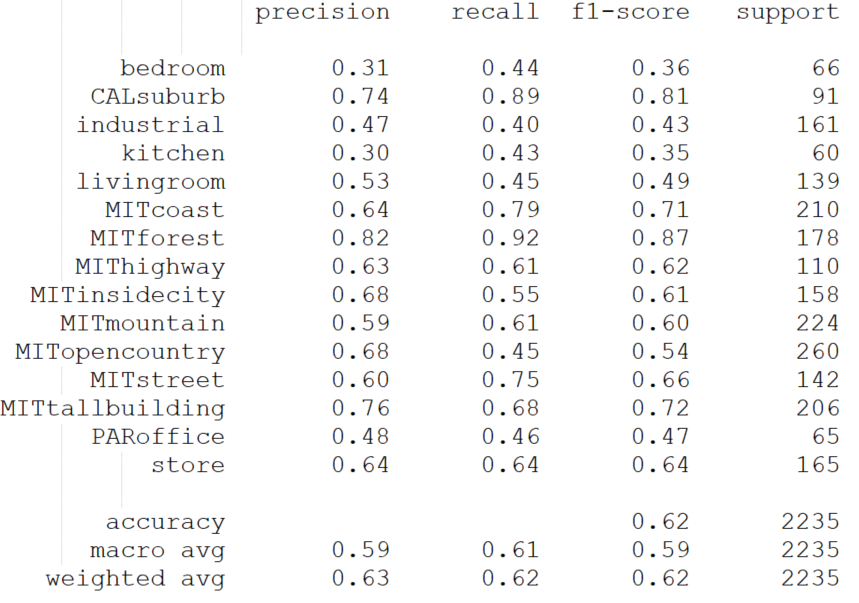
- 评估预测结果,并生成分类报告和输出混淆矩阵
算法简介
SIFT特征
Harris角点不具有尺度不变性,SIFT特征具有尺度不变性。

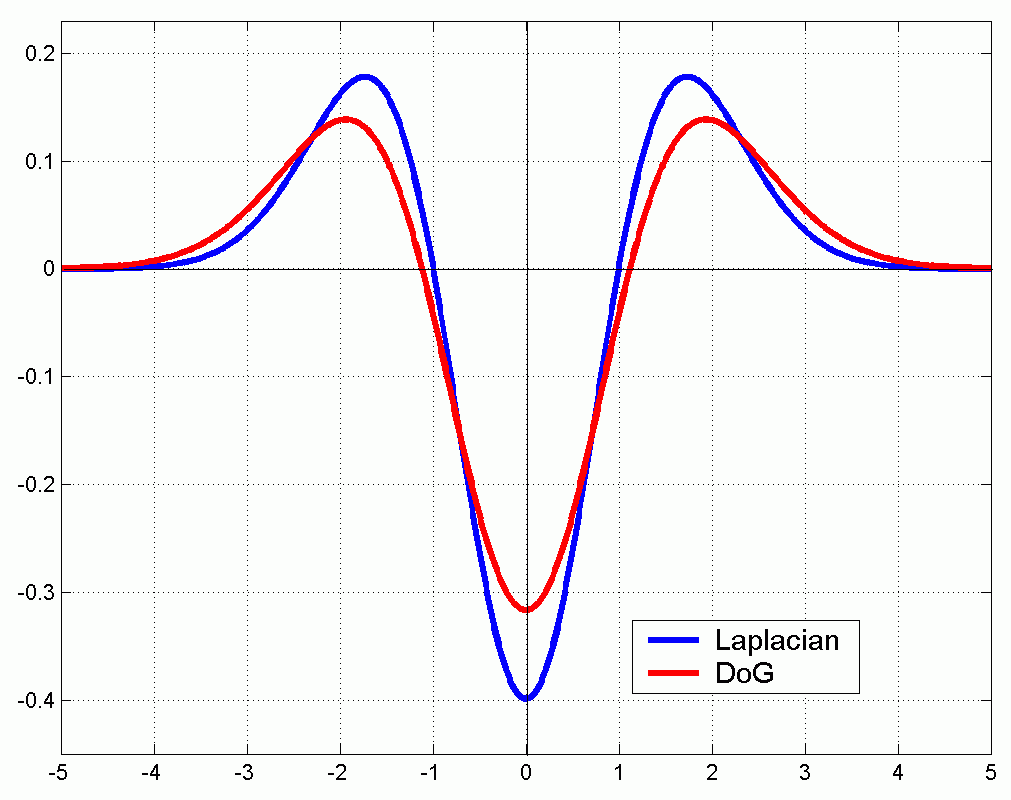
在已有的坐标的基础上增加尺度坐标,将信号与拉普拉斯核(高斯核的二阶导)做卷积, 表示高斯核中的方差。在某一点处,只有当 取到与之契合的值时卷积结果的极值点的绝对值最大。
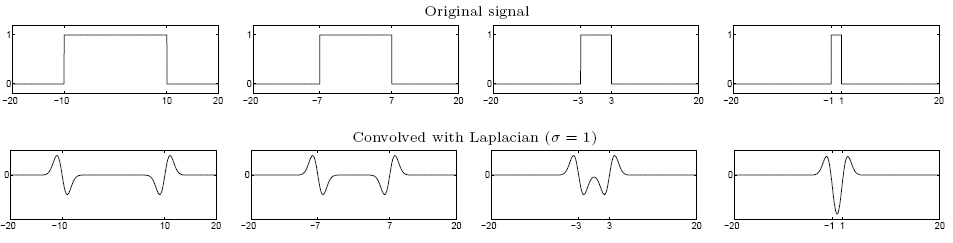
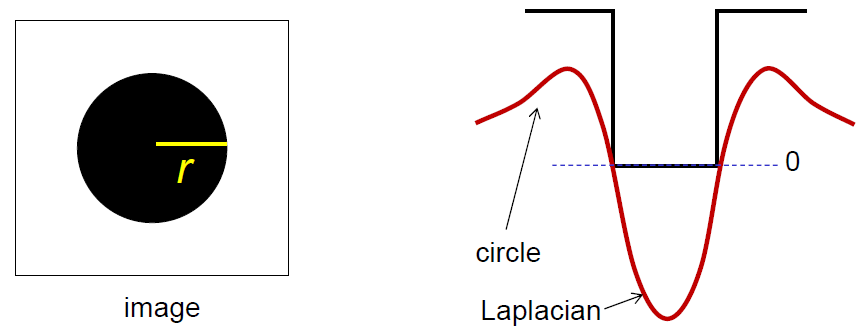
如上图,当 等于拉普拉斯核在零平面上的圆截面的半径时,两者卷积的绝对值最大,此时有 。
当图像的尺度改变时,与其契合的 的值也会随之改变,且始终满足上述关系,那么我们只需要找到这个 ,就能够推出尺度该点改变后的 。
通过在尺度金字塔找到极值点,得到该点的 ,当图片尺度改变时,新图中的对应点在新的 下仍会取到极值。在新旧图上该点处画两个对应尺度的圆,框出的信息是相同的,可以理解为与拉普拉斯核的卷积相当于信号的线性组合。
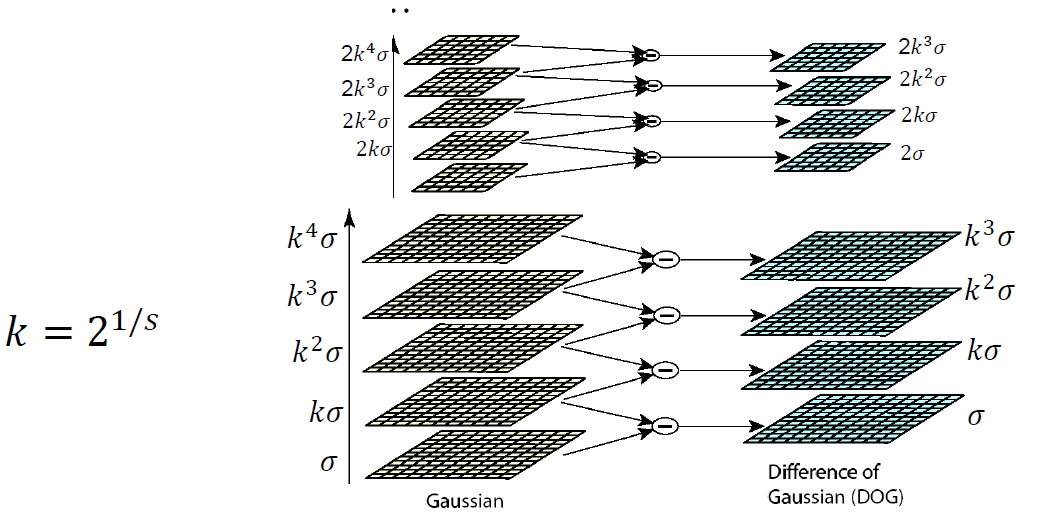
但由于要求得尺度空间就必须遍历所有的 ,导致若使用拉普拉斯核的复杂度无法优化,所以SIFT特征使用 来近似,这种差分得形式使得能够使用已有的卷积结果求得新的结果,且高斯核满足 的特殊性质使得能够用更小的核代替大核,效率进一步提升。
最终形成如下图的尺度空间,每个点与空间中相邻的26个点比较,得到极值点,就是SIFT的关键点。
求出SIFT框出的区域的二阶矩矩阵,对角化后不断压缩特征值更小的方向的框,再求解二阶矩矩阵,不断循环直到两个对角元素值相同。将SIFT从圆形变为椭圆形,使其能够满足仿射不变性。


当比较两张图上的对应的SIFT特征时则要先将两个SIFT特征都归一化为圆。
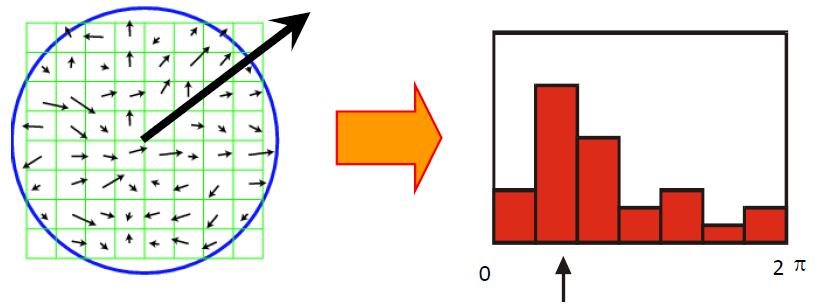
为了消除旋转导致的歧义,在SIFT框出的区域中求梯度直方图,个数最多的方向即是整个SIFT特征的方向,将SIFT倒转对应角度。
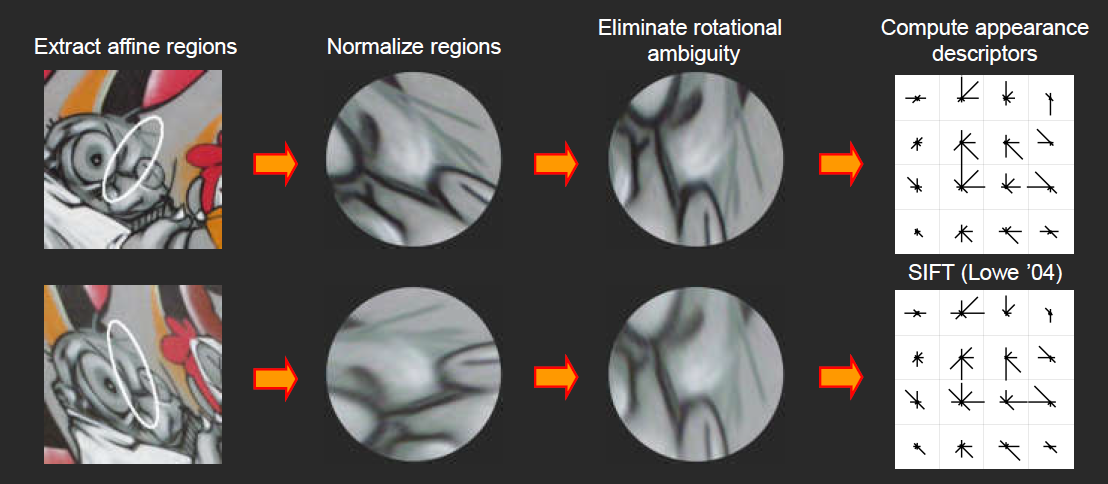
SIFT描述符:SIFT进行如上的归一化为圆,且消除了旋转后,将框出的区域分为 的 个小块,每块内统计 个方向区间的梯度直方图,拼接得到 维的向量,即 SIFT描述符。
SPM
Spatial pyramid representation
词袋模型一个很大的缺陷在于它只关注个数但不关注顺序,相同元素的集合打乱后仍会被视为相同。
SPM将一张图片分割为若干块,各个块单独表示,再拼接起来,得到整张图片的表示结果。
实验结果
将所有SIFT特征点聚类形成词典后,对于一个特征点求解它所在类别时,使用 KNN 优化。
求解SPM时遍历SIFT特征点,将它计入各个level中包含它的块的直方图中。