https://atcoder.jp/contests/abc175/tasks
E - Picking Goods
题意:一张nm的网格,有k格里有物品,价值为 vi,从左上角走到右下角,只能向下或向右走,可以拿或不拿格子里的物品,问最大价值。
dp
很简单的dp,写这题的题解不是为了怎么记做这题,而是犯的错误太蠢了。
1
2
3
4
| for (int i = 0; i <= n; i++)
for (int j = 0; j <= m; j++)
for (int x = 0; x <= 3; x++)
dp[i][j][k] = -inf;
|
调了半天的错误就是上面这个,由于题目里有 k,所以第三重循环我这里用了 x,但是在赋值时却还是用了k。
但是!由于第三维大小只有4,所以这样赋值会导致赋值到不知道什么地方去!!也并不是循环的。
赋值还在dp数组里还好,但是如果到了其他地方,比如 a 数组里而那个a又恰好会用到或者后面会用到的地址,那么就会导致错误!!!
以后再也不能犯这么傻逼的错了!
下面是正确代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
| #include<bits/stdc++.h>
using namespace std;
#define ll long long
const int INF = 0x3f3f3f3f;
const ll inf = 0x3f3f3f3f3f3f3f3f;
const int N = 2e6 + 10;
const ll mod = 1e9 + 7;
int n, m, k;
ll a[3010][3010];
ll dp[3010][3010][4];
int main() {
scanf("%d%d%d", &n, &m, &k);
for (int i = 1; i <= k; i++) {
int x, y;
scanf("%d%d", &x, &y);
scanf("%lld", &a[x][y]);
}
dp[1][1][0] = 0; if (a[1][1] >= 0)dp[1][1][1] = a[1][1];
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
if (i == 1 && j == 1)continue;
dp[i][j][0] = max(dp[i][j][0], dp[i][j - 1][0]);
for (int x = 0; x <= 3; x++)dp[i][j][0] = max(dp[i][j][0], dp[i - 1][j][x]), dp[i][j][1] = max(dp[i][j][1], dp[i - 1][j][x] + a[i][j]);
for (int x = 1; x <= min(j, 3); x++) {
dp[i][j][x] = max(dp[i][j][x], max(dp[i][j - 1][x], dp[i][j - 1][x - 1] + a[i][j]));
}
}
}
ll ans = 0;
for (int i = 0; i <= 3; i++)ans = max(ans, dp[n][m][i]);
printf("%lld\n", ans);
return 0;
}
|
F - Making Palindrome
题意:给定 n 个字符串,各自有代价,使用多次的代价等于使用次数乘代价。问拼出回文串的最少代价。
看了好久大佬的代码才懂
bfs
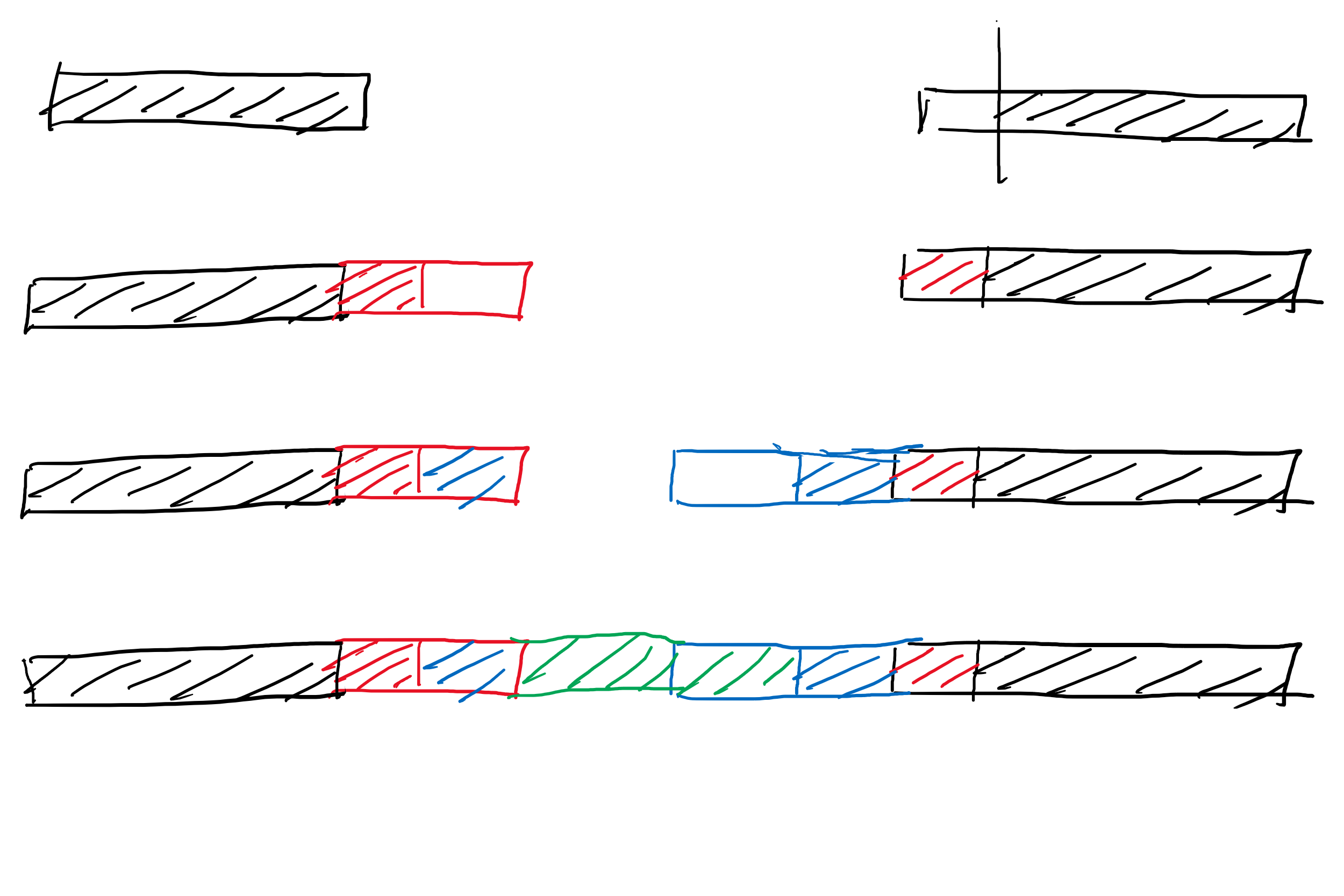
这是在不断向内拼接,直到成为回文串。
如上图,初始为空,假设先添加了左边的串,再添加了右边的串,这时发现左边和右边阴影部分对称相等,而右边还有一部分没有对称(空白部分)。下一步,又添加了红色边框的字符串,这时发现红色阴影部分对称相等。再下一步,添加蓝色边框的字符串,发现又有一部分蓝色阴影对称相等。再下一步,添加了绿色边框的字符串,发现新添加的这个绿色边框和上一步剩下的蓝色边框整个都对称,那么这拼起来就成了回文串。
由于是不断向内拼接,所以在外侧已经知道对称相等的部分(即每一步的阴影部分)都可以不要了,只留下空白部分用于下一次的比较。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
| #include<bits/stdc++.h>
using namespace std;
#define ll long long
const int INF = 0x3f3f3f3f;
const ll inf = 0x3f3f3f3f3f3f3f3f;
const int N = 2e6 + 10;
const ll mod = 1e9 + 7;
int n;
ll c[N];
string s[100];
typedef pair<string, string>pss;
map<pss, ll>d;
struct X
{
string a, b;
ll di;
bool operator<(const X&b)const {
return di > b.di;
}
};
bool ck(string a, string b, string c) {
if (a.empty())a = c;
else {
b = c;
reverse(b.begin(), b.end());
}
int x = min(a.length(), b.length());
if (a.substr(0, x) != b.substr(0, x))return false;
return true;
}
pss merge(string a, string b, string c) {
if (a.empty())a = c;
else {
b = c;
reverse(b.begin(), b.end());
}
int x = min(a.length(), b.length());
a = a.substr(x);
b = b.substr(x);
string rb = b;
reverse(rb.begin(), rb.end());
string tmp = a + rb;
string rtmp = tmp;
reverse(rtmp.begin(), rtmp.end());
if (tmp == rtmp)return pss("", "");
return pss(a, b);
}
ll bfs() {
priority_queue<X>q;
q.push(X{ "","",0 });
while (!q.empty()) {
X tp = q.top(); q.pop();
string a = tp.a, b = tp.b; ll di = tp.di;
if (d.count(pss(a, b)) && d[pss(a, b)] < di)continue;
if (di > 0 && a.empty() && b.empty())return di;
for (int i = 1; i <= n; i++) {
if (ck(a, b, s[i])) {
pss p = merge(a, b, s[i]);
if (!d.count(p) || d[p] > di + c[i]) {
d[p] = di + c[i];
q.push(X{ p.first,p.second,d[p] });
}
}
}
}
return -1;
}
int main() {
ios::sync_with_stdio(false);
cin >> n;
for (int i = 1; i <= n; i++)cin >> s[i] >> c[i];
printf("%lld\n", bfs());
return 0;
}
|







