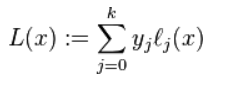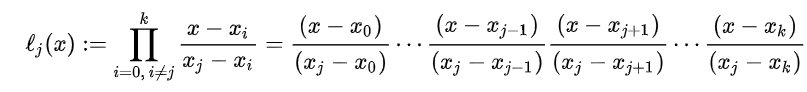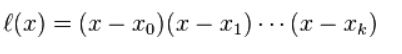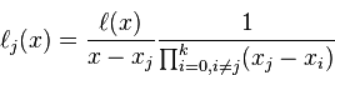模板

数学

 

大整数

 

 加减乘除，取模，逻辑运算符，输入，输出，绝对值，幂

 

class DividedByZeroException {};

class BigInteger {
private:
	vector<char> digits;
	bool sign;          //  true for positive, false for negitive
	void trim();        //  remove zeros in tail, but if the value is 0, keep only one:)
public:
	BigInteger(int);    // construct with a int integer
	BigInteger(string&);
	BigInteger();
	BigInteger(const BigInteger&);
	BigInteger operator=(const BigInteger& op2);

	BigInteger    abs() const;
	BigInteger    pow(int a);

	//binary operators

	friend BigInteger operator+=(BigInteger&, const BigInteger&);
	friend BigInteger operator-=(BigInteger&, const BigInteger&);
	friend BigInteger operator*=(BigInteger&, const BigInteger&);
	friend BigInteger operator/=(BigInteger&, const BigInteger&) throw(DividedByZeroException);
	friend BigInteger operator%=(BigInteger&, const BigInteger&) throw(DividedByZeroException);

	friend BigInteger operator+(const BigInteger&, const BigInteger&);
	friend BigInteger operator-(const BigInteger&, const BigInteger&);
	friend BigInteger operator*(const BigInteger&, const BigInteger&);
	friend BigInteger operator/(const BigInteger&, const BigInteger&) throw(DividedByZeroException);
	friend BigInteger operator%(const BigInteger&, const BigInteger&) throw(DividedByZeroException);


	//uniary operators
	friend BigInteger operator-(const BigInteger&);   //negative

	friend BigInteger operator++(BigInteger&);        //++v
	friend BigInteger operator++(BigInteger&, int);   //v++
	friend BigInteger operator--(BigInteger&);        //--v
	friend BigInteger operator--(BigInteger&, int);   //v--

	friend bool operator>(const BigInteger&, const BigInteger&);
	friend bool operator<(const BigInteger&, const BigInteger&);
	friend bool operator==(const BigInteger&, const BigInteger&);
	friend bool operator!=(const BigInteger&, const BigInteger&);
	friend bool operator>=(const BigInteger&, const BigInteger&);
	friend bool operator<=(const BigInteger&, const BigInteger&);

	friend ostream& operator<<(ostream&, const BigInteger&);   //print the BigInteger
	friend istream& operator>>(istream&, BigInteger&);         // input the BigInteger

public:
	static const BigInteger ZERO;
	static const BigInteger ONE;
	static const BigInteger TEN;
};
const BigInteger BigInteger::ZERO = BigInteger(0);
const BigInteger BigInteger::ONE = BigInteger(1);
const BigInteger BigInteger::TEN = BigInteger(10);


BigInteger::BigInteger() {
	sign = true;
}


BigInteger::BigInteger(int val) { // construct with a int integer
	if (val >= 0) {
		sign = true;
	}

	else {
		sign = false;
		val *= (-1);
	}

	do {
		digits.push_back((char)(val % 10));
		val /= 10;
	} while (val != 0);
}


BigInteger::BigInteger(string& def) {
	sign = true;

	for (string::reverse_iterator iter = def.rbegin(); iter < def.rend(); iter++) {
		char ch = (*iter);

		if (iter == def.rend() - 1) {
			if (ch == '+') {
				break;
			}

			if (ch == '-') {
				sign = false;
				break;
			}
		}

		digits.push_back((char)((*iter) - '0'));
	}

	trim();
}

void BigInteger::trim() {
	vector<char>::reverse_iterator iter = digits.rbegin();

	while (!digits.empty() && (*iter) == 0) {
		digits.pop_back();
		iter = digits.rbegin();
	}

	if (digits.size() == 0) {
		sign = true;
		digits.push_back(0);
	}
}


BigInteger::BigInteger(const BigInteger& op2) {
	sign = op2.sign;
	digits = op2.digits;
}


BigInteger BigInteger::operator=(const BigInteger& op2) {
	digits = op2.digits;
	sign = op2.sign;
	return (*this);
}


BigInteger BigInteger::abs() const {
	if (sign) {
		return *this;
	}

	else {
		return -(*this);
	}
}

BigInteger BigInteger::pow(int a) {
	BigInteger res(1);

	for (int i = 0; i < a; i++) {
		res *= (*this);
	}

	return res;
}

//binary operators
BigInteger operator+=(BigInteger& op1, const BigInteger& op2) {
	if (op1.sign == op2.sign) {     //只处理相同的符号的情况，异号的情况给-处理
		vector<char>::iterator iter1;
		vector<char>::const_iterator iter2;
		iter1 = op1.digits.begin();
		iter2 = op2.digits.begin();
		char to_add = 0;        //进位

		while (iter1 != op1.digits.end() && iter2 != op2.digits.end()) {
			(*iter1) = (*iter1) + (*iter2) + to_add;
			to_add = ((*iter1) > 9);    // 大于9进一位
			(*iter1) = (*iter1) % 10;
			iter1++;
			iter2++;
		}

		while (iter1 != op1.digits.end()) {    //
			(*iter1) = (*iter1) + to_add;
			to_add = ((*iter1) > 9);
			(*iter1) %= 10;
			iter1++;
		}

		while (iter2 != op2.digits.end()) {
			char val = (*iter2) + to_add;
			to_add = (val > 9);
			val %= 10;
			op1.digits.push_back(val);
			iter2++;
		}

		if (to_add != 0) {
			op1.digits.push_back(to_add);
		}

		return op1;
	}

	else {
		if (op1.sign) {
			return op1 -= (-op2);
		}

		else {
			return op1 = op2 - (-op1);
		}
	}

}

BigInteger operator-=(BigInteger& op1, const BigInteger& op2) {
	if (op1.sign == op2.sign) {     //只处理相同的符号的情况，异号的情况给+处理
		if (op1.sign) {
			if (op1 < op2) { // 2 - 3
				return  op1 = -(op2 - op1);
			}
		}

		else {
			if (-op1 > -op2) { // (-3)-(-2) = -(3 - 2)
				return op1 = -((-op1) - (-op2));
			}

			else {           // (-2)-(-3) = 3 - 2
				return op1 = (-op2) - (-op1);
			}
		}

		vector<char>::iterator iter1;
		vector<char>::const_iterator iter2;
		iter1 = op1.digits.begin();
		iter2 = op2.digits.begin();

		char to_substract = 0;  //借位

		while (iter1 != op1.digits.end() && iter2 != op2.digits.end()) {
			(*iter1) = (*iter1) - (*iter2) - to_substract;
			to_substract = 0;

			if ((*iter1) < 0) {
				to_substract = 1;
				(*iter1) += 10;
			}

			iter1++;
			iter2++;
		}

		while (iter1 != op1.digits.end()) {
			(*iter1) = (*iter1) - to_substract;
			to_substract = 0;

			if ((*iter1) < 0) {
				to_substract = 1;
				(*iter1) += 10;
			}

			else {
				break;
			}

			iter1++;
		}

		op1.trim();
		return op1;
	}

	else {
		if (op1 > BigInteger::ZERO) {
			return op1 += (-op2);
		}

		else {
			return op1 = -(op2 + (-op1));
		}
	}
}
BigInteger operator*=(BigInteger& op1, const BigInteger& op2) {
	BigInteger result(0);

	if (op1 == BigInteger::ZERO || op2 == BigInteger::ZERO) {
		result = BigInteger::ZERO;
	}

	else {
		vector<char>::const_iterator iter2 = op2.digits.begin();

		while (iter2 != op2.digits.end()) {
			if (*iter2 != 0) {
				deque<char> temp(op1.digits.begin(), op1.digits.end());
				char to_add = 0;
				deque<char>::iterator iter1 = temp.begin();

				while (iter1 != temp.end()) {
					(*iter1) *= (*iter2);
					(*iter1) += to_add;
					to_add = (*iter1) / 10;
					(*iter1) %= 10;
					iter1++;
				}

				if (to_add != 0) {
					temp.push_back(to_add);
				}

				int num_of_zeros = iter2 - op2.digits.begin();

				while (num_of_zeros--) {
					temp.push_front(0);
				}

				BigInteger temp2;
				temp2.digits.insert(temp2.digits.end(), temp.begin(), temp.end());
				temp2.trim();
				result = result + temp2;
			}

			iter2++;
		}

		result.sign = ((op1.sign && op2.sign) || (!op1.sign && !op2.sign));
	}

	op1 = result;
	return op1;
}

BigInteger operator/=(BigInteger& op1, const BigInteger& op2) throw(DividedByZeroException) {
	if (op2 == BigInteger::ZERO) {
		throw DividedByZeroException();
	}

	BigInteger t1 = op1.abs(), t2 = op2.abs();

	if (t1 < t2) {
		op1 = BigInteger::ZERO;
		return op1;
	}

	//现在 t1 > t2 > 0
	//只需将 t1/t2的结果交给result就可以了
	deque<char> temp;
	vector<char>::reverse_iterator iter = t1.digits.rbegin();

	BigInteger temp2(0);

	while (iter != t1.digits.rend()) {
		temp2 = temp2 * BigInteger::TEN + BigInteger((int)(*iter));
		char s = 0;

		while (temp2 >= t2) {
			temp2 = temp2 - t2;
			s = s + 1;
		}

		temp.push_front(s);
		iter++;
	}

	op1.digits.clear();
	op1.digits.insert(op1.digits.end(), temp.begin(), temp.end());
	op1.trim();
	op1.sign = ((op1.sign && op2.sign) || (!op1.sign && !op2.sign));
	return op1;
}

BigInteger operator%=(BigInteger& op1, const BigInteger& op2) throw(DividedByZeroException) {
	return op1 -= ((op1 / op2) * op2);
}

BigInteger operator+(const BigInteger& op1, const BigInteger& op2) {
	BigInteger temp(op1);
	temp += op2;
	return temp;
}
BigInteger operator-(const BigInteger& op1, const BigInteger& op2) {
	BigInteger temp(op1);
	temp -= op2;
	return temp;
}

BigInteger operator*(const BigInteger& op1, const BigInteger& op2) {
	BigInteger temp(op1);
	temp *= op2;
	return temp;

}

BigInteger operator/(const BigInteger& op1, const BigInteger& op2) throw(DividedByZeroException) {
	BigInteger temp(op1);
	temp /= op2;
	return temp;
}

BigInteger operator%(const BigInteger& op1, const BigInteger& op2) throw(DividedByZeroException) {
	BigInteger temp(op1);
	temp %= op2;
	return temp;
}

//uniary operators
BigInteger operator-(const BigInteger& op) {  //negative
	BigInteger temp = BigInteger(op);
	temp.sign = !temp.sign;
	return temp;
}

BigInteger operator++(BigInteger& op) {   //++v
	op += BigInteger::ONE;
	return op;
}

BigInteger operator++(BigInteger& op, int x) { //v++
	BigInteger temp(op);
	++op;
	return temp;
}

BigInteger operator--(BigInteger& op) {   //--v
	op -= BigInteger::ONE;
	return op;
}

BigInteger operator--(BigInteger& op, int x) { //v--
	BigInteger temp(op);
	--op;
	return temp;
}

bool operator<(const BigInteger& op1, const BigInteger& op2) {
	if (op1.sign != op2.sign) {
		return !op1.sign;
	}

	else {
		if (op1.digits.size() != op2.digits.size())
			return (op1.sign && op1.digits.size() < op2.digits.size())
			|| (!op1.sign && op1.digits.size() > op2.digits.size());

		vector<char>::const_reverse_iterator iter1, iter2;
		iter1 = op1.digits.rbegin();
		iter2 = op2.digits.rbegin();

		while (iter1 != op1.digits.rend()) {
			if (op1.sign &&  *iter1 < *iter2) {
				return true;
			}

			if (op1.sign &&  *iter1 > *iter2) {
				return false;
			}

			if (!op1.sign &&  *iter1 > *iter2) {
				return true;
			}

			if (!op1.sign &&  *iter1 < *iter2) {
				return false;
			}

			iter1++;
			iter2++;
		}

		return false;
	}
}
bool operator==(const BigInteger& op1, const BigInteger& op2) {
	if (op1.sign != op2.sign || op1.digits.size() != op2.digits.size()) {
		return false;
	}

	vector<char>::const_iterator iter1, iter2;
	iter1 = op1.digits.begin();
	iter2 = op2.digits.begin();

	while (iter1 != op1.digits.end()) {
		if (*iter1 != *iter2) {
			return false;
		}

		iter1++;
		iter2++;
	}

	return true;
}

bool operator!=(const BigInteger& op1, const BigInteger& op2) {
	return !(op1 == op2);
}

bool operator>=(const BigInteger& op1, const BigInteger& op2) {
	return (op1 > op2) || (op1 == op2);
}

bool operator<=(const BigInteger& op1, const BigInteger& op2) {
	return (op1 < op2) || (op1 == op2);
}

bool operator>(const BigInteger& op1, const BigInteger& op2) {
	return !(op1 <= op2);
}

ostream& operator<<(ostream& stream, const BigInteger& val) {  //print the BigInteger
	if (!val.sign) {
		stream << "-";
	}

	for (vector<char>::const_reverse_iterator iter = val.digits.rbegin(); iter != val.digits.rend(); iter++) {
		stream << (char)((*iter) + '0');
	}

	return stream;
}

istream& operator>>(istream& stream, BigInteger& val) {   //Input the BigInteger
	string str;
	stream >> str;
	val = BigInteger(str);
	return stream;
}

int main(){
	string s = "0012032039243283298329";
	BigInteger a = s, b = 1000007;
	cout << a%b;
	return 0;
}

 

分数高精度

 

typedef long long ll
struct frac
{
	ll x, y;
	bool operator<(const frac& b) const {
		return ll(x)*(b.y) < ll(y)*(b.x);
	}
	frac operator*(const frac& b)
	{
		return frac(x*b.x, y*b.y);
	}
	bool operator==(const frac& b) const {
		return ll(x)*(b.y) == ll(y)*(b.x);
	}
	frac(ll a, ll b) : x(ll(a)), y(ll(b)) {}
};
struct point
{
	frac x, y;
	bool operator<(const point& b) const {
		return x == b.x ? y < b.y : x < b.x;
	}
	bool operator==(const point& b) const {
		return x == b.x && y == b.y;
	}
	point(ll a, ll b, ll c, ll d) : x(a, b), y(c, d)	//x = a / b, y = c / d
	{
		/*ll m = gcd(abs(x.x), abs(x.y));			//可能T
		if(m)x.x /= m; x.y /= m;
		m = gcd(abs(y.x), abs(y.y));
		if(m)y.x /= m; y.y /= m;*/
        
        /*if (x.y == 0 && x.x != 0)x.x = 1;			//如果分母为0有意义，要加上
		if (y.y == 0 && y.x != 0)y.x = 1;*/
        
		if (x.y < 0) x.x = -x.x, x.y = -x.y;		//不要改，分数判断大小时正负号
		if (y.y < 0) y.x = -y.x, y.y = -y.y;
	}
};

 

模

 

inline int Add(int x, int y) {
	x += y;
	return x % mod;
}
inline int Sub(int x, int y) {
	x -= y;
	while (x < 0)x += mod;
	return x % mod;
}
inline int Mul(int x, int y) {
	return 1ll * x*y%mod;
}

 

博弈打表

 

f(局面 x) --> 面对局面x，胜利or失败?
{
    边界判断
        返回边界结果

    for (所有走法k)
    {
        走一步k-->局面y
        res = f(y)
        # 走法k会导致对方失败，说明是必胜点
        if res is 失败
            return 胜利
        回退局面-->局面x
    }
    # 所有的走法都是对方胜，说明是必败点
    return 失败
}

 

线性基

 

struct Linear_Basis
{
	ll b[63], nb[63], tot, len;	//共len个基，(1ll<<len)个不同的异或和值，包括0

	void init()
	{
		tot = 0;
		memset(b, 0, sizeof(b));
		memset(nb, 0, sizeof(nb));
	}

	bool ins(ll x)//插入
	{
		for (int i = 62; i >= 0; i--)
			if (x&(1ll << i))
			{
				if (!b[i]) { b[i] = x; len++; break; }
				x ^= b[i];
			}
		return x > 0;
	}

	ll Max()//所有可能异或中最大
	{
		ll res = 0;
		for (int i = 62; i >= 0; i--)
			res = max(res, res^b[i]);
		return res;
	}

	ll Min()//所有可能异或中最小
	{
		for (int i = 0; i <= 62; i++)
			if (b[i]) return b[i];
		return -1;
	}
    
    	ll Max(ll res)//所有可能异或中最大
	{
		for (int i = 62; i >= 0; i--)
			res = max(res, res^b[i]);
		return res;
	}

	ll Min(ll res)//所有可能异或中最小
	{
		for (int i = 62; i >= 0; i--)
			res = min(res, res^b[i]);
		return res;
	}

	void rebuild()
	{
		for (int i = 62; i >= 0; i--)
			for (int j = i - 1; j >= 0; j--)
				if (b[i] & (1LL << j)) b[i] ^= b[j];
		for (int i = 0; i <= 62; i++)
			if (b[i]) nb[tot++] = b[i];
	}

	ll Kth_Min(ll k) //所有可能异或中k小
	{	
		rebuild();
		ll res = 0;
		for (int i = 62; i >= 0; i--)
			if (k&(1LL << i)) res ^= nb[i];
		return res;
	}

} LB;

 

扩展欧几里得

 

int exgcd(int a, int b, ll& x, ll& y) {
	if (b == 0) {
		x = 1;
		y = 0;
		return a;
	}
	int t = exgcd(b, a%b, x, y);
	ll tmp = x;
	x = y;
	y = tmp - (a / b)*y;
	return t;
}

 

埃氏筛

 

const int N = 1e5 + 50;
int prime[N];
bool is_prime[N];
int sieve(int n) {
	int p = 0;
	memset(is_prime, true, sizeof(is_prime));
	is_prime[0] = is_prime[1] = false;
	for (int i = 2; i <= n; i++) {
		if (is_prime[i]) {
			prime[p++] = i;
			for (int j = 2 * i; j <= n; j+=i) {
				is_prime[j] = false;
			}
		}
	}
	return p;
}

 

欧拉筛

 

int prime[N];     //记录质数
bool is_prime[N];
int vis[N];      //记录最小质因子
int euler_sieve(int n) {
	int cnt = 0;
	memset(vis, 0, sizeof(vis));
	memset(prime, 0, sizeof(prime));
	for (int i = 2; i <= n; i++) {
		if (!vis[i]) { vis[i] = i; prime[cnt++] = i; is_prime[i] = true; }    //vis[]记录x的最小质因子
		for (int j = 0; j < cnt; j++) {
			if (i*prime[j] > n)  break;
			vis[i*prime[j]] = prime[j];              //vis[]记录x的最小质因子
			if (i%prime[j] == 0)
				break;
		}
	}
	return cnt;
}

 

求因数个数d[i]

ll p[N], d[N], num[N];
int v[N], tot;
void pre() {
  d[1] = 1;
  for (int i = 2; i <= n; ++i) {
    if (!v[i]) v[i] = 1, p[++tot] = i, d[i] = 2, num[i] = 1;
    for (int j = 1; j <= tot && i <= n / p[j]; ++j) {
      v[p[j] * i] = 1;
      if (i % p[j] == 0) {
        num[i * p[j]] = num[i] + 1;
        d[i * p[j]] = d[i] / num[i * p[j]] * (num[i * p[j]] + 1);
        break;
      } else {
        num[i * p[j]] = 1;
        d[i * p[j]] = d[i] * 2;
      }
    }
  }
}

求因数和f[i]

ll g[N], f[N], p[N];
int v[N], tot;
void pre() {
  g[1] = f[1] = 1;
  for (int i = 2; i <= n; ++i) {
    if (!v[i]) v[i] = 1, p[++tot] = i, g[i] = i + 1, f[i] = i + 1;
    for (int j = 1; j <= tot && i <= n / p[j]; ++j) {
      v[p[j] * i] = 1;
      if (i % p[j] == 0) {
        g[i * p[j]] = g[i] * p[j] + 1;
        f[i * p[j]] = f[i] / g[i] * g[i * p[j]];
        break;
      } else {
        f[i * p[j]] = f[i] * f[p[j]];
        g[i * p[j]] = 1 + p[j];
      }
    }
  }
  for (int i = 1; i <= n; ++i) f[i] = (f[i - 1] + f[i]) % mod;
}

 

拉格朗日插值法

 

$L(x)$ ：$x$ 的函数值 $f(x)$。

或：

 

欧拉函数

 

$$\varphi(n)=n\prod_{p|n\\p\in prime}(1-\frac{1}{p})$$

$O(n)$

ll phi[N], prime[N], p_sz, d;
bool vis[N];
void get_phi(int n) {
	phi[1] = 1;
	for (int i = 2; i <= n; i++) {
		if (!vis[i]) {
			prime[p_sz++] = i;
			phi[i] = i - 1;
		}
		for (ll j = 0; j < p_sz && (d = i * prime[j]) <= n; ++j) {
			vis[d] = 1;
			if (i % prime[j] == 0) {
				phi[d] = phi[i] * prime[j];
				break;
			}
			else phi[d] = phi[i] * (prime[j] - 1);
		}
	}
}

$O(\sqrt n)$

ll euler_Phi(ll n) {
	ll ans = n;
	for (ll i = 2; i*i <= n; i++) {
		if (n%i == 0) {
			ans = ans / i * (i - 1);
			while (n%i == 0) n /= i;
		}
	}
	if (n > 1) ans = ans / n * (n - 1);
	return ans;
}

 

逆元

 

 限制：b和mod互质

#include<bits/stdc++.h>
using namespace std;
int b,x,y,mod,gcd; 
inline int exgcd(int a,int b,int &x,int &y)
{
    if(b==0)
    {
        x=1,y=0;
        return a;
    }
    int ret=exgcd(b,a%b,x,y);
    int t=x;x=y,y=t-(a/b)*y;
    return ret;
}
int main()
{
    cin>>b>>mod;
    gcd=exgcd(b,mod,x,y);
    if(gcd!=1)printf("not exist\n");
    else printf("%d\n",(x%mod+mod)%mod);
    return 0;
}

 注意：返回的时候可以改成(x+mod)%mod，因为扩展欧几里得算法算出来的x应该不会太大.

 

 限制：mod为质数

#include<bits/stdc++.h>
using namespace std;
int b,mod; 
inline int ksm(int a,int b)
{
    int ret=1;
    a%=mod;
    while(b)
    {
        if(b&1)ret=(ret*a)%mod;
        a=(a*a)%mod;
        b>>=1;
    }
    return ret;
}
int main()
{
    cin>>b>>mod;
    cout<<ksm(b,mod-2);
    return 0;
}

 

线性求逆元

 限制：mod是质数

 逆元不存在的时候会输出0

ll inv[N];
void init() {
	inv[0] = inv[1] = 1;
	for (ll i = 2; i < N; i++)
		inv[i] = (mod - mod / i)*inv[mod%i] % mod;
}

 

阶乘逆元

ll fac[N], inv[N];
ll power(ll a, int x) {
	ll ans = 1;
	while (x) {
		if (x & 1) ans = (ans * a) % mod;
		a = (a * a) % mod;
		x >>= 1;
	}
	return ans;
}
void init() {
	fac[0] = 1;
	for (int i = 1; i < N; i++) {
		fac[i] = fac[i - 1] * i %mod;
	}
	inv[N - 1] = power(fac[N - 1], mod - 2);
	for (int i = N - 2; i >= 0; i--) {
		inv[i] = inv[i + 1] * (i + 1) % mod;
	}
}
ll C(int n, int k) {
	if (n < k)return 0;
	return fac[n] * inv[k] % mod*inv[n - k] % mod;
}

 

欧拉降幂

 

$$a^b \equiv\begin{cases} a^{b％\phi(m)}　　　　(gcd(a,m)==1)\\ a^b 　　　　　　(gcd(a,m) !=1 ＆b<\phi(m))\\ a^{b％\phi(m)+\phi(m)}　(gcd(a,m)!=1＆b\geq\phi(m)) \end{cases}(mod 　m)$$

扩展欧拉定理

$$a^b\equiv a^{b％\phi(m)+\phi(m)}(mod 　m)$$

可以直接用扩展欧拉定理代替欧拉降幂

ll Mod(ll x, ll mod) {
	return x < mod ? x : (x % mod + mod);
}
ll q_pow(ll a, ll b, ll mod) {
	ll ans = 1;
	while (b) {
		if (b & 1)ans = Mod((ans*a),mod);
		a = Mod(a*a, mod);
		b >>= 1;
	}
	return ans;
}
ll euler_phi(ll n)
{
	ll m = (ll)sqrt(n + 0.5);
	ll ans = n;
	for (ll i = 2; i <= m; i++)
	{
		if (n % i == 0)
		{
			ans = ans / i * (i - 1);
			while (n % i == 0)  n /= i;        //除尽
		}
	}
	if (n > 1)  ans = ans / n * (n - 1);    //剩下的不为1,也是素数
	return ans;
}

 

中国剩余定理

 

$x \mod m_i=r_i$

$x=x_iM_iM_i^{-1},M_i=\frac{m_1m_2\cdots m_n}{m_i}$

ll crt(ll* m, ll* r, ll n) {
	if (!n)return 0;
	ll M = m[0], R = r[0], x, y, d;
	for (int i = 1; i < n; i++) {
		d = exgcd(M, m[i], x, y);
		if ((r[i] - R) % d)return -1;
		x = (r[i] - R) / d * x % (m[i] / d);
		R += x * M;
		M = M / d * m[i];
		R %= M;
	}
	return R >= 0 ? R : R + M;
}

 

扩展中国剩余定理

 

$x \mod M_i=C_i$

ll x, y;
ll gcd(ll a, ll b) {
	if (a < b)swap(a, b);
	return b == 0 ? a : gcd(b, a % b);
}
ll exgcd(ll a, ll b, ll &x, ll &y) {
	if (b == 0) { x = 1, y = 0; return a; }
	ll r = exgcd(b, a % b, x, y), tmp;
	tmp = x; x = y; y = tmp - (a / b) * y;
	return r;
}
ll inv(ll a, ll b) {
	ll r = exgcd(a, b, x, y);
	while (x < 0) x += b;
	return x;
}
ll excrt(ll* M, ll* C, int n) {
	for (int i = 2; i <= n; i++) {
		ll M1 = M[i - 1], M2 = M[i], C2 = C[i], C1 = C[i - 1], T = gcd(M1, M2);
		if ((C2 - C1) % T != 0) return -1;
		M[i] = (M1 * M2) / T;
		C[i] = (inv(M1 / T, M2 / T) * (C2 - C1) / T) % (M2 / T) * M1 + C1;
		C[i] = (C[i] % M[i] + M[i]) % M[i];
	}
	return C[n];
}

 

Pollard-Rho

#define rg register
#define RP(i,a,b) for(register int i=a;i<=b;++i)
#define DRP(i,a,b) for(register int i=a;i>=b;--i)
#define fre(z) freopen(z".in","r",stdin),freopen(z".out","w",stdout)
typedef double db;
#define lll __int128
ll gcd(ll a, ll b) {
	if (b == 0) return a;
	return gcd(b, a % b);
}

ll quick_pow(ll x, ll p, ll mod) {
	ll ans = 1;
	while (p) {
		if (p & 1) ans = (lll)ans * x % mod;
		x = (lll)x * x % mod;
		p >>= 1;
	}
	return ans;
}

bool Miller_Rabin(ll p) {
	if (p < 2) return 0;
	if (p == 2) return 1;
	if (p == 3) return 1;
	ll d = p - 1, r = 0;
	while (!(d & 1)) ++r, d >>= 1;
	for (ll k = 0; k < 10; ++k) {
		ll a = rand() % (p - 2) + 2;
		ll x = quick_pow(a, d, p);
		if (x == 1 || x == p - 1) continue;
		for (int i = 0; i < r - 1; ++i) {
			x = (lll)x * x % p;
			if (x == p - 1) break;
		}
		if (x != p - 1) return 0;
	}
	return 1;
}

ll f(ll x, ll c, ll n) { return ((lll)x * x + c) % n; }

ll Pollard_Rho(ll x) {
	ll s = 0, t = 0;
	ll c = (ll)rand() % (x - 1) + 1;
	int step = 0, goal = 1;
	ll val = 1;
	for (goal = 1;; goal <<= 1, s = t, val = 1) {
		for (step = 1; step <= goal; ++step) {
			t = f(t, c, x);
			val = (lll)val * abs(t - s) % x;
			if ((step % 127) == 0) {
				ll d = gcd(val, x);
				if (d > 1) return d;
			}
		}
		ll d = gcd(val, x);
		if (d > 1) return d;
	}
}

ll fac[1010][100], fcnt[1010];
void get_fac(int id, ll n, ll cc = 19260817) {
	if (n == 4) { fac[id][fcnt[id]++] = 2; fac[id][fcnt[id]++] = 2; return; }
	if (Miller_Rabin(n)) { fac[id][fcnt[id]++] = n; return; }
	ll p = n;
	while (p == n) p = Pollard_Rho(n);
	get_fac(id, p); get_fac(id, n / p);
}
void go_fac(int id, ll n) { fcnt[id] = 0; if (n > 1) get_fac(id, n); }

 

迪利克雷前缀和

$O(n\log\log n)$

迪利克雷前缀和

$$b_i=\sum_{d|i}a_d\\$$

已知 $a$，求 $b$

tot = get_prime(n)	//prime[0~~tot-1]
for(int i = 0; i < tot && prime[i] <= n; ++ i) {
    for(int j = 1; j * prime[i] <= n; ++ j) {
        a[j * prime[i]] += a[j];
    }
}

迪利克雷后缀和

$$b_i=\sum_{i|j\wedge j\le n}a_j\\$$

已知 $a$，求 $b$

tot = get_prime(n)	//prime[0~~tot-1]
for(int i = 0; i < tot && prime[i] <= n; ++ i) {
    for(int j = n / prime[i]; j ; -- j) {
        a[j] += a[j * prime[i]];
    }
}

倒推迪利克雷前缀和

$$b_i=\sum_{d|i}a_d\\$$

已知 $b$，求 $a$

tot = get_prime(n)	//prime[0~~tot-1]
for(int i = tot - 1; i >= 0; -- i) {
    for(int j = n / prime[i]; j ; -- j) {
        a[j * prime[i]] -= a[j];
    }
}

倒推迪利克雷后缀和

$$b_i=\sum_{i|j\wedge j\le n}a_j\\$$

已知 $b$，求 $a$

tot = get_prime(n)	//prime[0~~tot-1]
for(int i = tot - 1; i >= 0; -- i) {
    for(int j = 1; j * prime[i] <= n; ++ j) {
        a[j] -= a[j * prime[i]];
    }
}

 

FFT

 

多项式系数表示，点值表示

• n 需补成 2 的幂 （n 必须超过 a 和 b 的最高指数之和）

typedef double LD;
const LD PI = acos(-1);
struct C {
    LD r, i;
    C(LD r = 0, LD i = 0): r(r), i(i) {}
};
C operator + (const C& a, const C& b) {
    return C(a.r + b.r, a.i + b.i);
}
C operator - (const C& a, const C& b) {
    return C(a.r - b.r, a.i - b.i);
}
C operator * (const C& a, const C& b) {
    return C(a.r * b.r - a.i * b.i, a.r * b.i + a.i * b.r);
}

void FFT(C x[], int n, int p) {
    for (int i = 0, t = 0; i < n; ++i) {
        if (i > t) swap(x[i], x[t]);
        for (int j = n >> 1; (t ^= j) < j; j >>= 1);
    }
    for (int h = 2; h <= n; h <<= 1) {
        C wn(cos(p * 2 * PI / h), sin(p * 2 * PI / h));
        for (int i = 0; i < n; i += h) {
            C w(1, 0), u;
            for (int j = i, k = h >> 1; j < i + k; ++j) {
                u = x[j + k] * w;
                x[j + k] = x[j] - u;
                x[j] = x[j] + u;
                w = w * wn;
            }
        }
    }
    if (p == -1)
        FOR (i, 0, n)
            x[i].r /= n;
}

void conv(C a[], C b[], C c[], int n) {
    FFT(a, n, 1);
    FFT(b, n, 1);
    FOR (i, 0, n)
        c[i] = a[i] * b[i];
    FFT(c, n, -1);
}
//字符串匹配(n+m)log(n+m)
//01串最小失配数
int ans = INF;
C a[N<<2], b[N<<2], c[N<<2];
int sumT, sum[N], P[N];
void solve(char s[], char t[]){
    int n = strlen(s), m = strlen(t);
	int len = 1;
	int mx = n + m;
	while (len <= mx) len <<= 1; //mx为卷积后最大下标
    for (int i = 0; i < n; i++)a[i] = C(s[i] - '0', 0);
	for (int i = 0; i < m; i++)b[i] = C(t[i] - '0', 0);
	for (int i = 0; i < m; i++)sumT += b[i].r;
	sum[0] = a[0].r;
	for (int i = 1; i < n; i++)sum[i] = sum[i - 1] + a[i].r;
	reverse(b, b + m);
	conv(a, b, c, len);
	for (int x = 0; x <= n - m; x++) {
		P[x] = sumT + sum[x + m - 1] - sum[max(0, x - 1)] - 2 * (int)(c[x + m - 1].r + 0.5);//精度
		ans = min(ans, P[x]);
	}
}

 

const double PI = acos(-1.0);
struct Complex {
  double x, y;
  Complex(double _x = 0.0, double _y = 0.0) {
    x = _x;
    y = _y;
  }
  Complex operator-(const Complex &b) const {
    return Complex(x - b.x, y - b.y);
  }
  Complex operator+(const Complex &b) const {
    return Complex(x + b.x, y + b.y);
  }
  Complex operator*(const Complex &b) const {
    return Complex(x * b.x - y * b.y, x * b.y + y * b.x);
  }
};
/*
 * 进行 FFT 和 IFFT 前的反置变换
 * 位置 i 和 i 的二进制反转后的位置互换
 *len 必须为 2 的幂
 */
void change(Complex y[], int len) {
  int i, j, k;
  for (i = 1, j = len / 2; i < len - 1; i++) {
    if (i < j) swap(y[i], y[j]);
    // 交换互为小标反转的元素，i<j 保证交换一次
    // i 做正常的 + 1，j 做反转类型的 + 1，始终保持 i 和 j 是反转的
    k = len / 2;
    while (j >= k) {
      j = j - k;
      k = k / 2;
    }
    if (j < k) j += k;
  }
}
/*
 * 做 FFT
 *len 必须是 2^k 形式
 *on == 1 时是 DFT，on == -1 时是 IDFT
 */
void fft(Complex y[], int len, int on) {	//0-len-1
  change(y, len);
  for (int h = 2; h <= len; h <<= 1) {
    Complex wn(cos(2 * PI / h), sin(on * 2 * PI / h));
    for (int j = 0; j < len; j += h) {
      Complex w(1, 0);
      for (int k = j; k < j + h / 2; k++) {
        Complex u = y[k];
        Complex t = w * y[k + h / 2];
        y[k] = u + t;
        y[k + h / 2] = u - t;
        w = w * wn;
      }
    }
  }
  if (on == -1) {
    for (int i = 0; i < len; i++) {
      y[i].x /= len;
    }
  }
}

 

NTT

 

$n$ 需补成 $2$ 的幂 （ $n$ 必须超过 $a$ 和 $b$ 的最高指数之和）

• 先进行 NTT_init() 操作， $G$ 为 $MOD$ 原根

NTT 素数表及对应原根

MOD	G
40961	3
65537	3
786433	10
5767169	3
7340033	3
23068673	3
104857601	3
167772161	3
469762049	3
998244353	3
1004535809	3
2013265921	31
2281701377	3
3221225473	5
75161927681	3

#define MOD 998244353
#define G 3

const int N=2000010;

ll bin(ll x,ll n,ll mo)
{
    LL ret=mo!=1;
    for (x%=mo;n;n>>=1,x=x*x%mo)
        if (n&1) ret=ret*x%mo;
    return ret;
}

inline ll get_inv(ll x,ll p)
{
    return bin(x,p-2,p);
}

ll wn[N<<1],rev[N<<1];
int NTT_init(int n_)
{
    int step=0,n=1;
    for (;n<n_;n<<=1) step++;
    for (int i=1;i<n;i++)
        rev[i]=(rev[i>>1]>>1)|((i&1)<<(step-1));
    int g=bin(G,(MOD-1)/n,MOD);
    wn[0]=1;
    for (int i=1;i<=n;i++)
        wn[i]=wn[i-1]*g%MOD;
    return n;
}

void NTT(ll a[],int n,int f)
{
    for (int i=0;i<n;i++)
        if (i<rev[i]) swap(a[i],a[rev[i]]);
    for (int k=1;k<n;k<<=1)
    {
        for (int i=0;i<n;i+=(k<<1))
        {
            int t=n/(k<<1);
            for (int j=0;j<k;j++)
            {
                LL w=f==1?wn[t*j]:wn[n-t*j];
                LL x=a[i+j];
                LL y=a[i+j+k]*w%MOD;
                a[i+j]=(x+y)%MOD;
                a[i+j+k]=(x-y+MOD)%MOD;
            }
        }
    }
    if (f==-1)
    {
        ll ninv=get_inv(n,MOD);
        for (int i=0;i<n;i++)
            a[i]=a[i]*ninv%MOD;
    }
}

 

FMT

 

$f[x]=\sum f[y]$，其中 $y$ 为 $x$ 的真子集

void FMT(LL *f, LL flag){	//flag=1 FMT, flag=-1 IFMT
    for (LL i=0; i<len; i++)
        for (LL j=0; j<(1<<len); j++)
            if ((j>>i&1)==0) f[j|1<<i]+=(~flag?f[j]:-f[j]);
}

 

FWT

 

$C_k=\sum_{i|j=k}A_i*B_j$

$C_k=\sum_{i\&j=k}A_i*B_j$

$C_k=\sum_{i\wedge j=k}A_i*B_j$

$FWT(A|B)=FWT(A)\times FWT(B)$

$FWT(A\&B)=FWT(A)\times FWT(B)$

$FWT(A\oplus B)=FWT(A)\times FWT(B)$

如果不要取模就把乘2的逆元改为除2。

N 补为2的幂次

void FWT_or(int *a,int N,int opt)	//0-N-1
{
    for(int i=1;i<N;i<<=1)
        for(int p=i<<1,j=0;j<N;j+=p)
            for(int k=0;k<i;++k)
                if(opt==1)a[i+j+k]=(a[j+k]+a[i+j+k])%MOD;
                else a[i+j+k]=(a[i+j+k]+MOD-a[j+k])%MOD;
}
void FWT_and(int *a,int N,int opt)	//0-N-1
{
    for(int i=1;i<N;i<<=1)
        for(int p=i<<1,j=0;j<N;j+=p)
            for(int k=0;k<i;++k)
                if(opt==1)a[j+k]=(a[j+k]+a[i+j+k])%MOD;
                else a[j+k]=(a[j+k]+MOD-a[i+j+k])%MOD;
}
void FWT_xor(int *a,int N,int opt)	//0-N-1
{
    for(int i=1;i<N;i<<=1)
        for(int p=i<<1,j=0;j<N;j+=p)
            for(int k=0;k<i;++k)
            {
                int X=a[j+k],Y=a[i+j+k];
                a[j+k]=(X+Y)%MOD;a[i+j+k]=(X+MOD-Y)%MOD;
                if(opt==-1)a[j+k]=1ll*a[j+k]*inv2%MOD,a[i+j+k]=1ll*a[i+j+k]*inv2%MOD;
            }
}

 

矩阵快速幂

 

如果a不能ll就改成int

struct Mat {
    int a[N][N];
    int r, c;

    Mat(int _r = N, int _c = N) {
        r = _r, c = _c;
        for (int i = 0; i < r; i++)for (int j = 0; j < c; j++)a[i][j] = 0;
    }

    Mat operator*(Mat b) const {
        Mat ans(r, b.c);
        for (int i = 0; i < r; ++i)
            for (int j = 0; j < c; ++j)
                if (a[i][j])
                    for (int k = 0; k < b.c; ++k)ans.a[i][k] = (ans.a[i][k] + 1ll * a[i][j] * b.a[j][k]) % mod;
        return ans;
    }
};
Mat pow(Mat a, ll n) {
	Mat res(a.r, a.c);
	for (int i = 0; i < a.r; i++)
		res.a[i][i] = 1;
	while (n) {
		if (n & 1) res = res * a;;
		a = a * a;
		n >>= 1;
	}
	return res;
}

 

整除分块

 

#include<bits/stdc++.h>
using namespace std;
int main(){
    long long n,ans=0;
    cin >> n;
    for(long long l=1,r;l<=n;l=r+1){
        r = n/(n/l);            //计算r，让分块右移
        ans += (r-l+1)*(n/l);   //求和
        cout << l <<""<< r <<": "<< n/r << endl;  //打印分块
    }
    cout << ans;               //打印和
}

 

莫比乌斯函数

 

int mu[N], p[N], tot;
bool flg[N];
void getMu() {
	mu[1] = 1;
	for (int i = 2; i < N; ++i) {
		if (!flg[i]) p[++tot] = i, mu[i] = -1;
		for (int j = 1; j <= tot && i * p[j] < N; ++j) {
			flg[i * p[j]] = 1;
			if (i % p[j] == 0) {
				mu[i * p[j]] = 0;
				break;
			}
			mu[i * p[j]] = -mu[i];
		}
	}
}

 

单纯形

 

min { b x }
A^T x >= c
x >= 0

以上要对偶先转为标准型，即交换系数，矩阵转置

要求有基本解，也就是 x 为零向量可行

v 要为 0，n 表示向量长度，m 表示约束个数

不保证整数解

// max { c x }
// A x <= b
// x >= 0
namespace lp {
	int n, m;
	double a[M][N], b[M], c[N], v;

	void pivot(int l, int e) {
		b[l] /= a[l][e];
		FOR(j, 0, n) if (j != e) a[l][j] /= a[l][e];
		a[l][e] = 1 / a[l][e];

		FOR(i, 0, m)
			if (i != l && fabs(a[i][e]) > 0) {
				b[i] -= a[i][e] * b[l];
				FOR(j, 0, n)
					if (j != e) a[i][j] -= a[i][e] * a[l][j];
				a[i][e] = -a[i][e] * a[l][e];
			}
		v += c[e] * b[l];
		FOR(j, 0, n) if (j != e) c[j] -= c[e] * a[l][j];
		c[e] = -c[e] * a[l][e];
	}
	double simplex() {
		v = 0;
		while (1) {
			int e = -1, l = -1;
			FOR(i, 0, n) if (c[i] > eps) { e = i; break; }
			if (e == -1) return v;
			double t = 1e18;
			FOR(i, 0, m)
				if (a[i][e] > eps && t > b[i] / a[i][e]) {
					t = b[i] / a[i][e];
					l = i;
				}
			if (l == -1) return INF;
			pivot(l, e);
		}
	}
}

 

高斯消元

 

a是增广矩阵

线性方程组整数类型解

int a[N][N];//增广矩阵
int x[N];//解集
bool freeX[N];//标记是否为自由变元
int GCD(int a,int b){
    return !b?a:GCD(b,a%b);
}
int LCM(int a,int b){
    return a/GCD(a,b)*b;
}
int Gauss(int equ,int var){//返回自由变元个数
    /*初始化*/
    for(int i=0;i<=var;i++){
        x[i]=0;
        freeX[i]=true;
    }
 
    /*转换为阶梯阵*/
    int col=0;//当前处理的列
    int row;//当前处理的行
    for(row=0;row<equ&&col<var;row++,col++){//枚举当前处理的行
        int maxRow=row;//当前列绝对值最大的行
        for(int i=row+1;i<equ;i++){//寻找当前列绝对值最大的行
            if(abs(a[i][col])>abs(a[maxRow][col]))
                maxRow=i;
        }
        if(maxRow!=row){//与第row行交换
            for(int j=row;j<var+1;j++)
                swap(a[row][j],a[maxRow][j]);
        }
        if(a[row][col]==0){//col列第row行以下全是0，处理当前行的下一列
            row--;
            continue;
        }
 
        for(int i=row+1;i<equ;i++){//枚举要删去的行
            if(a[i][col]!=0){
                int lcm=LCM(abs(a[i][col]),abs(a[row][col]));
                int ta=lcm/abs(a[i][col]);
                int tb=lcm/abs(a[row][col]);
                if(a[i][col]*a[row][col]<0)//异号情况相加
                    tb=-tb;
                for(int j=col;j<var+1;j++) {
                    a[i][j]=a[i][j]*ta-a[row][j]*tb;
                }
            }
        }
    }
 
    /*求解*/
    //无解：化简的增广阵中存在(0,0,...,a)这样的行，且a!=0
    for(int i=row;i<equ;i++)
        if (a[i][col]!=0)
            return -1;
 
    //无穷解: 在var*(var+1)的增广阵中出现(0,0,...,0)这样的行
    int temp=var-row;//自由变元有var-row个
    if(row<var)//返回自由变元数
        return temp;
 
    //唯一解: 在var*(var+1)的增广阵中形成严格的上三角阵
    for(int i=var-1;i>=0;i--){//计算解集
        int temp=a[i][var];
        for(int j=i+1;j<var;j++){
            if(a[i][j]!=0)
                temp-=a[i][j]*x[j];
        }
        if(temp%a[i][i]!=0)//有浮点数解，无整数解
            return -2;
        x[i]=temp/a[i][i];
    }
    return 0;
}
 
int main(){
    int equ,var;//equ个方程，var个变元
    while(scanf("%d%d",&equ,&var)!=EOF) {
 
        memset(a,0,sizeof(a));
        for(int i=0;i<equ;i++)//输入增广矩阵
            for(int j=0;j<var+1;j++)
                scanf("%d",&a[i][j]);
 
 
        int freeNum=Gauss(equ,var);//自由元个数
        if(freeNum==-1)//无解
            printf("无解\n");
        else if(freeNum==-2)//有浮点数解无整数解
            printf("无整数解\n");
        else if(freeNum>0){//有无穷多解
            printf("有无穷多解，自由变元个数为%d\n",freeNum);
            for(int i=0;i<var;i++){
                if(freeX[i])
                    printf("x%d是自由变元\n",i+1);
                else
                    printf("x%d=%d\n",i+1,x[i]);
            }
        }
        else{//有唯一解
            for(int i=0;i<var;i++)
                printf("x%d=%d\n",i+1,x[i]);
        }
        printf("\n");
    }
    return 0;
}

 

线性方程组浮点类型解

const double eps = 1e-15;
double a[110][110];
double x[110];
bool freeX[100];
int Gauss(int equ, int var) {
	for (int i = 0; i <= var; i++) {
		x[i] = 0;
		freeX[i] = true;
	}
	int col = 0;
	int row;
	for (row = 0; row < equ&&col < var; row++, col++) {
		int maxRow = row;
		for (int i = row + 1; i < equ; i++) {
			if (abs(a[i][col]) > abs(a[maxRow][col]))
				maxRow = i;
		}
		if (maxRow != row) {
			for (int j = row; j < var + 1; j++)
				swap(a[row][j], a[maxRow][j]);
		}
		if (fabs(a[row][col]) < eps) {
			row--;
			continue;
		}
		for (int i = row + 1; i < equ; i++) {
			if (fabs(a[i][col]) > eps) {
				double temp = a[i][col] / a[row][col];
				for (int j = col; j < var + 1; j++)
					a[i][j] -= a[row][j] * temp;
				a[i][col] = 0;
			}
		}
	}
	for (int i = row; i < equ; i++)
		if (fabs(a[i][col]) > eps)
			return -1;
	int temp = var - row;
	if (row < var)
		return temp;
	for (int i = var - 1; i >= 0; i--) {
		double temp = a[i][var];
		for (int j = i + 1; j < var; j++)
			temp -= a[i][j] * x[j];
		x[i] = temp / a[i][i];
	}
	return 0;
}

 

double A[110][110], x[110];
void Gauss(int ne, int nv){
	int i, j;
	for (int ce = 0, cv = 0; cv < ne && cv < nv; ++ce, ++cv){
		int te = ce;
		for (i = ce; i < ne; ++i)
			if (fabs(A[i][cv]) > fabs(A[te][cv]))
				te = i;
		if (te != ce){
			for (j = cv; j <= nv; ++j)
				swap(A[ce][j], A[te][j]);
		}
		double bas = A[ce][cv];
		for (j = cv; j <= nv; ++j)
			A[ce][j] /= bas;
		for (i = ce + 1; i < ne; ++i){
			for (int j = cv + 1; j <= nv; ++j)
				A[i][j] -= A[i][cv] * A[ce][j];
		}
	}
	for (i = ne - 1; i >= 0; --i){
		x[i] = A[i][nv];
		for (j = i + 1; j < nv; ++j)
			x[i] -= x[j] * A[i][j];
		x[i] /= A[i][i];
	}
}

 

模线性方程组

int a[N][N];//增广矩阵
int x[N];//解集
bool freeX[N];//标记是否为自由变元
int GCD(int a,int b){
    return !b?a:GCD(b,a%b);
}
int LCM(int a,int b){
    return a/GCD(a,b)*b;
}
int Gauss(int equ,int var){//返回自由变元个数
    /*初始化*/
    for(int i=0;i<=var;i++){
        x[i]=0;
        freeX[i]=true;
    }
 
    /*转换为阶梯阵*/
    int col=0;//当前处理的列
    int row;//当前处理的行
    for(row=0;row<equ&&col<var;row++,col++){//枚举当前处理的行
        int maxRow=row;//当前列绝对值最大的行
        for(int i=row+1;i<equ;i++){//寻找当前列绝对值最大的行
            if(abs(a[i][col])>abs(a[maxRow][col]))
                maxRow=i;
        }
        if(maxRow!=row){//与第row行交换
            for(int j=row;j<var+1;j++)
                swap(a[row][j],a[maxRow][j]);
        }
        if(a[row][col]==0){//col列第row行以下全是0，处理当前行的下一列
            row--;
            continue;
        }
 
        for(int i=row+1;i<equ;i++){//枚举要删去的行
            if(a[i][col]!=0){
                int lcm=LCM(abs(a[i][col]),abs(a[row][col]));
                int ta=lcm/abs(a[i][col]);
                int tb=lcm/abs(a[row][col]);
                if(a[i][col]*a[row][col]<0)//异号情况相加
                    tb=-tb;
                for(int j=col;j<var+1;j++) {
                    a[i][j]=((a[i][j]*ta-a[row][j]*tb)%MOD+MOD)%MOD;
                }
            }
        }
    }
 
    /*求解*/
    //无解：化简的增广阵中存在(0,0,...,a)这样的行，且a!=0
    for(int i=row;i<equ;i++)
        if (a[i][col]!=0)
            return -1;
 
    //无穷解: 在var*(var+1)的增广阵中出现(0,0,...,0)这样的行
    int temp=var-row;//自由变元有var-row个
    if(row<var)//返回自由变元数
        return temp;
 
    //唯一解: 在var*(var+1)的增广阵中形成严格的上三角阵
    for(int i=var-1;i>=0;i--){//计算解集
        int temp=a[i][var];
        for(int j=i+1;j<var;j++){
            if(a[i][j]!=0)
                temp-=a[i][j]*x[j];
            temp=(temp%MOD+MOD)%MOD;//取模
        }
        while(temp%a[i][i]!=0)//外层每次循环都是求a[i][i]，它是每个方程中唯一一个未知的变量
            temp+=MOD;//a[i][i]必须为整数，加上周期MOD
        x[i]=(temp/a[i][i])%MOD;//取模
    }
    return 0;
}

 

异或方程组

int a[N][N];//增广矩阵
int x[N];//解集
int freeX[N];//自由变元
int Gauss(int equ,int var){//返回自由变元个数
    /*初始化*/
    for(int i=0;i<=var;i++){
        x[i]=0;
        freeX[i]=0;
    }
 
    /*转换为阶梯阵*/
    int col=0;//当前处理的列
    int num=0;//自由变元的序号
    int row;//当前处理的行
    for(row=0;row<equ&&col<var;row++,col++){//枚举当前处理的行
        int maxRow=row;//当前列绝对值最大的行
        for(int i=row+1;i<equ;i++){//寻找当前列绝对值最大的行
            if(abs(a[i][col])>abs(a[maxRow][col]))
                maxRow=i;
        }
        if(maxRow!=row){//与第row行交换
            for(int j=row;j<var+1;j++)
                swap(a[row][j],a[maxRow][j]);
        }
        if(a[row][col]==0){//col列第row行以下全是0，处理当前行的下一列
            freeX[num++]=col;//记录自由变元
            row--;
            continue;
        }
 
        for(int i=row+1;i<equ;i++){
            if(a[i][col]!=0){
                for(int j=col;j<var+1;j++){//对于下面出现该列中有1的行，需要把1消掉
                    a[i][j]^=a[row][j];
                }
            }
        }
    }
 
    /*求解*/
    //无解：化简的增广阵中存在(0,0,...,a)这样的行，且a!=0
    for(int i=row;i<equ;i++)
        if(a[i][col]!=0)
            return -1;
 
    //无穷解: 在var*(var+1)的增广阵中出现(0,0,...,0)这样的行
    int temp=var-row;//自由变元有var-row个
    if(row<var)//返回自由变元数
        return temp;
 
    //唯一解: 在var*(var+1)的增广阵中形成严格的上三角阵
    for(int i=var-1;i>=0;i--){//计算解集
        x[i]=a[i][var];
        for(int j=i+1;j<var;j++)
            x[i]^=(a[i][j]&&x[j]);
    }
    return 0;
}
int enumFreeX(int freeNum,int var){//枚举自由元，统计有解情况下1最少的个数
    int sta=(1<<(freeNum));//自由元的状态总数
    int res=INF;
    for(int i=0;i<sta;++i){//枚举状态
        int cnt=0;
        for(int j=0;j<freeNum;j++){//枚举自由元
            if(i&(1<<j)){
                cnt++;
                x[freeX[j]]=1;
            }else
                x[freeX[j]]=0;
        }
        for(int k=var-freeNum-1;k>=0;k--){//没有自由元的最下面一行
            int index=0;
            for(index=k;k<var;index++){//在当前行找到第一个非0自由元
                if(a[k][index])
                    break;
            }
            x[index]=a[k][var];
            for(int j=index+1;j<var;++j){//向后依次计算出结果
                if(a[k][j])
                    x[index]^=x[j];
            }
            cnt+=x[index];//若结果为1，则进行统计
        }
        res=min(res,cnt);
    }
    return res;
}
int main(){
    memset(a,0,sizeof(a));
 
    int equ,var;
    scanf("%d%d",&equ,&var);
    for(int i=0;i<equ;i++){//构造初始状态
 
    }
    for(int i=0;i<equ;i++)//最终状态
        scanf("%d",&a[i][var]);
 
    int freeNum=Gauss(equ,var);//获取自由元
    if(freeNum==-1)//无解
        printf("inf\n");
    else if(freeNum==0){//唯一解
        int res=0;
        for(int i=0;i<var;i++)
            res+=x[i];
        printf("%d\n",res);
    }
    else{//多个解
        int res=enumFreeX(freeNum,var);
        printf("%d\n",res);
    }
    return 0;
}

 

高斯消元求行列式

 

ll gauss(int n) {
    ll res = 1ll;
    for (int i = 1; i <= n; i++) {
        for (int j = i + 1; j <= n; j++) {
            while (K[j][i]) {
                int t = K[i][i] / K[j][i];
                for (int k = i; k <= n; k++)
                    K[i][k] = (K[i][k] - t * K[j][k] + mod) % mod;
                swap(K[i], K[j]);
                res = -res;
            }
        }
        res = (res*K[i][i]) % mod;
    }
    return (res + mod) % mod;
}

 

计算几何前置

struct Point{
	double x, y;
	Point(double x = 0, double y = 0) :x(x), y(y) {}
};
typedef Point Vector;
Vector operator+(Vector A, Vector B) { return Vector(A.x + B.x, A.y + B.y); }
Vector operator-(Point A, Point B) { return Vector(A.x - B.x, A.y - B.y); }
Vector operator*(Vector A, double p) { return Vector(A.x*p, A.y*p); }
Vector operator/(Vector A, double p) { return Vector(A.x / p, A.y / p); }
bool operator<(const Point& a, const Point& b) {
	return a.x < b.x || (a.x == b.x&&a.y < b.y);
}
const double eps = 1e-10;
int dcmp(double x) {
	if (fabs(x) < eps)return 0;
	else return x < 0 ? -1 : 1;
}
bool operator==(const Point& a, const Point& b) {
	return dcmp(a.x - b.x) == 0 && dcmp(a.y - b.y) == 0;
}
double Dot(Vector A, Vector B) { return A.x*B.x + A.y*B.y; }
double Length(Vector A) { return sqrt(Dot(A, A)); }
double Angle(Vector A, Vector B) { return acos(Dot(A, B) / Length(A) / Length(B)); }
double Cross(Vector A, Vector B) { return A.x*B.y - A.y*B.x; }
double Area(Point A, Point B, Point C) { return fabs(Cross(B - A, C - A)) / 2; }	//无向面积

 

凸包

double eps = 1e-10;
double add(double a, double b) {
	if (abs(a + b) < eps*(abs(a) + abs(b)))return 0;
	return a + b;
}
struct Point
{
	double x, y;
	Point() {}
	Point(double x, double y) :x(x), y(y) {}
	Point operator+(Point p) {
		return Point(add(x, p.x), add(y, p.y));
	}
	Point operator-(Point p) {
		return Point(add(x, -p.x), add(y, -p.y));
	}
	Point operator*(double d) {
		return Point(x*d, y*d);
	}
	double dot(Point p) {
		return add(x*p.x, y*p.y);
	}
	double cross(Point p) {
		return add(x*p.y, -y * p.x);
	}
};
bool cmp_x(const Point& p, const Point& q) {
	if (p.x != q.x)return p.x < q.x;
	return p.y < q.y;
}
vector<Point>convex_hull(Point* ps, int n, int flg = 1) {	// flag = 0 不严格(可以共线） flag = 1 严格
	sort(ps, ps + n, cmp_x);
	int k = 0;		//凸包的顶点数
	vector<Point>qs(n * 2);		//构造中的凸包
	//构造凸包下侧
	for (int i = 0; i < n; i++) {
		while (k > 1 && (qs[k - 1] - qs[k - 2]).cross(ps[i] - qs[k - 1]) < flg)k--;
		qs[k++] = ps[i];
	}
	//构造凸包上侧
	for (int i = n - 2, t = k; i >= 0; i--) {
		while (k > t && (qs[k - 1] - qs[k - 2]).cross(ps[i] - qs[k - 1]) < flg)k--;
		qs[k++] = ps[i];
	}
	qs.resize(k - 1);
	return qs;
}

 

最大空凸包

 

#include <bits/stdc++.h>
using namespace std;
const int N = 2e6 + 10;
int T;
int n, m;
double ans, dp[60][60];
struct Point {
	int x, y;
	Point(int x = 0, int y = 0) :x(x), y(y) {}
	int dis() { return x * x + y * y; }
}a[N], b[N], O;
typedef Point Vector;
Vector operator+(Vector A, Vector B) { return Vector(A.x + B.x, A.y + B.y); }
Vector operator-(Point A, Point B) { return Vector(A.x - B.x, A.y - B.y); }
bool operator<(const Point& a, const Point& b) {
	return a.x < b.x || (a.x == b.x&&a.y < b.y);
}
int Cross(Vector A, Vector B) { return A.x*B.y - A.y*B.x; }
double Area(Point A, Point B, Point C) { return fabs(Cross(B - A, C - A) * 0.5); }
bool cmp(Point A, Point B) {
	int a = Cross(A - O, B - O);
	if (a != 0)return a > 0;
	else return (A - O).dis() < (B - O).dis();
}
void solve() {
	memset(dp, 0, sizeof(dp));
	sort(b + 1, b + m + 1, cmp);
	for (int i = 1; i <= m; i++) {
		int j = i - 1;
		while (j && Cross(b[i] - O, b[j] - O) == 0)j--;
		int flg = (j == i - 1);
		while (j) {
			int k = j - 1;
			while (k && Cross(b[i] - b[k], b[j] - b[k]) > 0)k--;
			double tmp = Area(O, b[i], b[j]);
			if (k)tmp += dp[j][k];
			ans = max(ans, tmp);
			if (flg)dp[i][j] = tmp;
			j = k;
		}
		if (flg)for (int j = 2; j < i; j++)dp[i][j] = max(dp[i][j], dp[i][j - 1]);
	}
}
int main() {
	scanf("%d", &T);
	while (T--) {
		scanf("%d", &n);
		for (int i = 1; i <= n; i++)scanf("%d%d", &a[i].x, &a[i].y);
		ans = 0;
		for (int i = 1; i <= n; i++) {
			m = 0;
			O = a[i];
			for (int j = 1; j <= n; j++) {
				if (a[j].y > a[i].y || (a[j].y == a[i].y&&a[j].x > a[i].x))b[++m] = a[j];
			}
			solve();
		}
		printf("%.1f\n", ans);
	}
	return 0;
}

 

旋转卡壳

 

最大四边形面积

ll area(Point a, Point b, Point c) {
	return abs((a - b).cross(a - c));
}
ll rotating_calipers(vector<Point>& ps, int n) {
	ll res = 0;
	for (int i = 0; i < n; i++) {
		int p1 = (i + 1) % n;
		int p2 = (i + 3) % n;
		for (int j = (i + 2) % n; (j + 1) % n != i; j = (j + 1) % n) {
			while ((p1 + 1) % n != j && area(ps[p1], ps[i], ps[j]) < area(ps[(p1 + 1) % n], ps[i], ps[j])) {
				p1 = (p1 + 1) % n;
			}
			if (p2 == j)p2 = (p2 + 1) % n;
			while ((p2 + 1) % n != i && area(ps[p2], ps[i], ps[j]) < area(ps[(p2 + 1) % n], ps[i], ps[j])) {
				p2 = (p2 + 1) % n;
			}
			res = max(res, area(ps[p1], ps[i], ps[j]) + area(ps[p2], ps[i], ps[j]));
		}
	}
	return res;
}

 

杜教筛

 

$O(n^{2/3})$

$$\sum_{i=1}^n g(i)S(\lfloor\frac{n}{i}\rfloor)=\sum_{i=1}^n (f*g)(i)\\ S(n) = \sum_{i=1}^n (f*g)(i)-\sum_{i=2}^n g(i)\cdot S(\lfloor\frac{n}{i}\rfloor)\\$$

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define debug(x) cout << #x << ":\t" << x << endl;
const int INF = 0x3f3f3f3f;
const ll inf = 0x3f3f3f3f3f3f3f3f;
const int N = 5e6 + 10;
const ll mod = 998244353;
int T;
ll n;
ll mu[N], phi[N], prime[N];
bool vis[N]; int cnt;
void pre(ll n) {
	mu[1] = phi[1] = 1;
	for (ll i = 2; i <= n; i++) {
		if (!vis[i]) {
			prime[cnt++] = i;
			mu[i] = -1;
			phi[i] = i - 1;
		}
		ll d;
		for (int j = 0; j < cnt && (d = i * prime[j]) <= n; j++) {
			vis[d] = 1;
			if (i%prime[j] == 0) {
				mu[d] = 0;
				phi[d] = phi[i] * prime[j];
				break;
			}
			else {
				mu[d] = -mu[i];
				phi[d] = phi[i] * phi[prime[j]];
			}
		}
	}
	for (int i = 1; i <= n; i++)mu[i] += mu[i - 1], phi[i] += phi[i - 1];
}
map<ll, ll>smu, sp;
ll S_mu(ll n) {
	if (n <= 5e6)return mu[n];
	if (smu.count(n))return smu[n];
	ll ans = 0;
	for (ll l = 2, r; l <= n; l = r + 1) {
		r = n / (n / l);
		ans += (r - l + 1)*S_mu(n / l);
	}
	return smu[n] = 1ll - ans;
}
ll S_p(ll n) {
	if (n <= 5e6)return phi[n];
	if (sp.count(n))return sp[n];
	ll ans = 0;
	for (ll l = 2, r; l <= n; l = r + 1) {
		r = n / (n / l);
		ans += (r - l + 1)*S_p(n / l);
	}
	return sp[n] = (1 + n)*n / 2 - ans;
}
int main() {
	pre(5e6);
	scanf("%d", &T);
	while (T--) {
		scanf("%lld", &n);
		printf("%lld %lld\n", S_p(n), S_mu(n));
	}
	return 0;
}

 

min25筛

 

$O(\frac{n^\frac{3}{4}}{\log n})$

$f$ 要求前缀和的积性函数

$g$ 等于 $f$ 在质数时的式子

$G(i,j)$ 为 $≤i$ 的所有质数以及最小质因子 $>Pj$ 的合数的 $g$ 值之和

$S(i,j)$ 表示 $≤i$ 的所有最小质因子大于等于 $Pj$ 的数的 $f$ 值之和（质数的最小质因子为它自己）

$G(n,|P|)$ 或 $S(n,1)$ 为答案（代码里 $w[1]=n$）

$$G(i,0)=\sum_{k=2}^i g(k)$$

$$G(n,j)= \begin{cases} G(n,j-1)&P_j^2\gt n\\ G(n,j-1)-f(P_j)[G(\frac{n}{P_j},j-1)-\sum_{i=1}^{j-1}f(P_i)]&P_j^2\le n\\ \end{cases}$$

$$S(i,|P|)=G(i,|P|)\\$$

$$S(n,j)=G(n,|P|)-\sum_{i=1}^{j-1}f(P_i)+\sum_{k\ge j}\sum_{e\ge 1} f(P_k^e)S(\frac{n}{P_k^e},k+1)+f(P_k^{e+1})\\$$

$g$ 为素数和，$h$ 为素数个数，$S=g-h$

#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define debug(x) cout << #x << ":\t" << x << endl;
const int N = 2e6 + 10;
const int INF = 0x3f3f3f3f;
const ll inf = 0x3f3f3f3f3f3f3f3f;
const ll mod = 1e9 + 7;
const ll inv2 = (mod + 1) / 2;
ll n, sqr;
int vis[N], tot;
ll prime[N], sump[N];
void pre(ll n) {
	for (int i = 2; i <= n; i++) {
		if (!vis[i]) {
			prime[++tot] = i;
			sump[tot] = (sump[tot - 1] + i) % mod;
		}
		ll d;
		for (int j = 1; j <= tot && (d = i * prime[j]) <= n; j++) {
			vis[d] = 1;
			if (i%prime[j] == 0)break;
		}
	}
}
ll w[N]; int m;
ll g[N], h[N];
int id[2][N];
ll f(ll x, int y) {			//题目要对积性函数f求前缀和
	return x ^ y;
}
ll S(ll x, int j) {
	if (x <= 1 || x < prime[j])return 0;
	int k = (x <= sqr ? id[0][x] : id[1][n / x]);
	ll res = (g[k] - sump[j - 1] - h[k] + j - 1 + 2 * mod) % mod;
	//if (j == 1)res = (res + 2) % mod;		//这题n=2时计算结果不对，要修正
    										//其它题目不需要
	for (int i = j; i <= tot && prime[i] * prime[i] <= x; i++) {
		ll t = prime[i];
		for (int e = 1; t*prime[i] <= x; e++, t *= prime[i]) {
			res = (res + f(prime[i], e)*S(x / t, i + 1) % mod + f(prime[i], e + 1)) % mod;
		}
	}
	return res;
}
int main() {
	scanf("%lld", &n);
	sqr = (ll)sqrt(n);

	//预处理
	pre(sqr);

	//第一步
		//求G(n/x, 0)
	for (ll i = 1, j; i <= n; i = j + 1) {
		j = n / (n / i);
		w[++m] = n / i;
		if (w[m] <= sqr)id[0][w[m]] = m;
		else id[1][n / w[m]] = m;
		g[m] = w[m] % mod*((w[m] + 1) % mod) % mod*inv2 % mod;	//g := f_1
		g[m] = (g[m] - 1 + mod) % mod;
		h[m] = (w[m] - 1 + mod) % mod;							//h := f_2
	}
		//递推求G(n/x,|P|)
	for (int j = 1; j <= tot; j++) {
		for (int i = 1; i <= m && w[i] >= prime[j] * prime[j]; i++) {
			int k = (w[i] / prime[j] <= sqr ? id[0][w[i] / prime[j]] : id[1][n / (w[i] / prime[j])]);
			ll tmp = prime[j]*(g[k] + mod - sump[j - 1]) % mod;
			g[i] = (g[i] + mod - tmp) % mod;
			tmp = (h[k] - (j - 1) + mod) % mod;
			h[i] = (h[i] + mod - tmp) % mod;
		}
	}

	//第二步
	printf("%lld\n", (S(n, 1) + 1) % mod);
	return 0;
}

 

斯特林数

第一类斯特林数

• 将 $n$ 个两两不同的元素，划分为 $k$ 个非空圆排列的方案数。

• $s(n,k)=s(n-1,k-1)+(n-1)s(n-1,k)$

第二类斯特林数

• 将 $n$ 个两两不同的元素，划分为 $k$ 个非空子集的方案数。
• $S(n, k)=S(n-1,k-1)+kS(n-1, k)$

ll s[5010][5010];
void pres(int k) {
	s[0][0] = 1;
	for (int i = 1; i <= k; i++)
		for (int j = 1; j <= i; j++)
			s[i][j] = (s[i - 1][j - 1] + j * s[i - 1][j] % mod) % mod;
}

自然数幂次求和

$O(k^2)$

$$\sum_{a=1}^{n}a^k=\sum_{i=0}^{k}S(k,i)\frac{(n+1)!}{(i+1)(n-i)!}$$

ll cal(ll n, int k){
	if (n == 0) return 0;
	pres(k);
	ll ret = 0;
	for (int i = 0; i <= k && i <= n; i++){
		ll sum = s[k][i];
		for (ll j = n - i + 1; j <= n + 1; j++)
			if (j % (i + 1) == 0) sum = sum * ((j / (i + 1)) % mod) % mod;
			else sum = sum * (j%mod) % mod;
		ret = (ret + sum) % mod;
	}
	return ret;
}

 

数论

 

1. 小于n且与n互质的数的和=$\frac{n\cdot\phi (n)}{2}$

2. 原图 $(x,y) ->$ 新图 $(x+y,x-y)$ ：曼哈顿距离 -> 切比雪夫距离

   $(x,y)->(\frac{x+y}{2},\frac{x-y}{2})$，切比雪夫 -> 曼哈顿

3. 全错位排列（每个位置都和其下标不同的情况数）：$f(n)=(n−1)(f(n−1)+f(n−2)),f(1)=0,f(2)=1$

4. $f(i,j)=f(i-1,0)+f(i-1,1)+f(i-1,2)+\cdots +f(i-1,j)\\ =\sum_{k=0}^{j}f(i-1,k)\\=\frac{(i+j)!}{i!\cdot j!}$

5. Lucus定理：

   设 $p$ 为素数，且 $a,b\in N^*$，且 $a=a_kp^k+a_{k-1}p^{k-1}+\cdots a_1p+a_0$ ， $b=b_kp^k+b_{k-1}p^{k-1}+\cdots b_1p+b_0$，（即把 $a,b$ 变为 $p$ 进制下的表示），则 $C_a^b\equiv C_{a_k}^{b_k}\cdot C_{a_{k-1}}^{b_{k-1}}\cdots C_{a_0}^{b_0}(\mod p)$.

6. $(x_1,y_1)$ 绕 $(x_2,y_2)$ 旋转 $\theta$ 后坐标。极坐标求。

   $$\begin{cases} x=(x_1-x_2)\cos \theta-(y_1-y_2)\sin \theta+x_2\\ y=(y_1-y_2)\cos \theta+(x_1-x_2)\sin \theta+y_2\\ \end{cases}$$

7. $\varphi()$ 为欧拉函数

   $\sum_{d|n}\varphi(d)=n$

   $\varphi(n)=\sum_{d|n}d\cdot \mu(n/d)$

8. 莫比乌斯反演

   • $F(n)=\sum_{d|n}f(d)\implies f(n)=\sum_{d|n}\mu(d)\cdot F(\frac{n}{d})\implies f=\mu*F$
   • $f(d)=\sum_{d|n}g(n) \implies g(d)=\sum_{d|n}f(n)\cdot \mu(\frac{n}{d})$
   • $\mu*I=\epsilon, \epsilon(x)=[x==1],I(x)=1$
   • $I*\varphi = ID,ID(x)=x$.

9. $d(n)$：$n$ 的因数个数

   $$\begin{align} d(nm)&=\sum\limits_{x|n}\sum\limits_{y|m}[\gcd(x,y)==1]\\ d(ijk)&=\sum\limits_{x|i}\sum\limits_{y|j}\sum\limits_{z|k}[\gcd(x,y)=1][\gcd(y,z)=1][\gcd(x,z)=1]\\ &\vdots \end{align}$$

10. 斯特林公式： $n!\approx\sqrt{2\pi n}(\frac{n}{e})^n$

11. 二项式反演：

    1. $f(n)=\sum\limits_{i=0}^n(-1)^i{n\choose i}g(i)\Leftrightarrow g(n)=\sum\limits_{i=0}^n(-1)^i{n\choose i}f(i)$
    2. $f(n)=\sum\limits_{i=0}^n{n\choose i}g(i)\Leftrightarrow g(n)=\sum\limits_{i=0}^n(-1)^{n-i}{n\choose i}f(i)$ 常用
    3. $f(n)=\sum\limits_{i=n}^m{i\choose n}g(i)\Leftrightarrow g(n)=\sum\limits_{i=n}^m(-1)^{i-n}{i\choose n}f(i)$ 常用

12. 循环矩阵：每行由上一行右移得到。

    循环矩阵的线性组合及循环矩阵的乘积仍是循环矩阵。

13. 约瑟夫环：N个人编号为0，1，2，……，N-1，依次报数，每报到M-1时，杀掉那个人，求最后胜利者的编号。

    $f(N,M)=(f(N−1,M)+M)\%N$

14. prufer 序列：选出编号最小的叶子，把与他相连的节点编号加入序列，并删除该叶子。重复直到只剩下两个点。长度为 $n-2$，每点的出现次数等于它的度数 -1.

    Cayley定理：$n$ 个有标号的点能组成 $n^{n-2}$ 棵不同的树。

    扩展Cayley定理：$n$ 个有标号的点组成包含 $s$ 棵树的森林，有 $sn^{n-s-1}$ 种。

公式

一些数论公式

• 当 $x\geq\phi(p)$ 时有 $a^x\equiv a^{x \ mod \text{ }\phi(p) + \phi(p)}\pmod p$
• $\mu^2(n)=\sum_{d^2|n} \mu(d)$
• $\sum_{d|n} \varphi(d)=n$
• $\sum_{d|n} 2^{\omega(d)}=\sigma_0(n^2)$，其中 $\omega$ 是不同素因子个数
• $\sum_{d|n} \mu^2(d)=2^{\omega(d)}$

一些数论函数求和的例子

• $\sum_{i=1}^n i[gcd(i, n)=1] = \frac {n \varphi(n) + [n=1]}{2}$
• $\sum_{i=1}^n \sum_{j=1}^m [gcd(i,j)=x]=\sum_d \mu(d) \lfloor \frac n {dx} \rfloor \lfloor \frac m {dx} \rfloor$
• $\sum_{i=1}^n \sum_{j=1}^m gcd(i, j) = \sum_{i=1}^n \sum_{j=1}^m \sum_{d|gcd(i,j)} \varphi(d) = \sum_{d} \varphi(d) \lfloor \frac nd \rfloor \lfloor \frac md \rfloor$
• $S(n)=\sum_{i=1}^n \mu(i)=1-\sum_{i=1}^n \sum_{d|i,d < i}\mu(d) \overset{t=\frac id}{=} 1-\sum_{t=2}^nS(\lfloor \frac nt \rfloor)$
  • 利用 $[n=1] = \sum_{d|n} \mu(d)$
• $S(n)=\sum_{i=1}^n \varphi(i)=\sum_{i=1}^n i-\sum_{i=1}^n \sum_{d|i,d<i} \varphi(i)\overset{t=\frac id}{=} \frac {i(i+1)}{2} - \sum_{t=2}^n S(\frac n t)$
  • 利用 $n = \sum_{d|n} \varphi(d)$
• $\sum_{i=1}^n \mu^2(i) = \sum_{i=1}^n \sum_{d^2|n} \mu(d)=\sum_{d=1}^{\lfloor \sqrt n \rfloor}\mu(d) \lfloor \frac n {d^2} \rfloor$
• $\sum_{i=1}^n \sum_{j=1}^n gcd^2(i, j)= \sum_{d} d^2 \sum_{t} \mu(t) \lfloor \frac n{dt} \rfloor ^2 \ \overset{x=dt}{=} \sum_{x} \lfloor \frac nx \rfloor ^ 2 \sum_{d|x} d^2 \mu(\frac xd)$
• $\sum_{i=1}^n \varphi(i)=\frac 12 \sum_{i=1}^n \sum_{j=1}^n [i \perp j] - 1=\frac 12 \sum_{i=1}^n \mu(i) \cdot\lfloor \frac n i \rfloor ^2-1$

斐波那契数列性质

• $$\begin{pmatrix} f_{n+1} & f_{n} \\ f_{n} & f_{n-1} \\ \end{pmatrix}= \begin{pmatrix} 1 & 1 \\ 1 & 0 \\ \end{pmatrix}^{n}\\ \begin{pmatrix} f_{2n+1} & f_{2n} \\ f_{2n} & f_{2n-1} \\ \end{pmatrix}= \begin{pmatrix} 1 & 1 \\ 1 & 0 \\ \end{pmatrix}^{2n}\\ \Downarrow\\ \begin{pmatrix} f_{2n+1} & f_{2n} \\ f_{2n} & f_{2n-1} \\ \end{pmatrix}= \begin{pmatrix} f_{n+1} & f_{n} \\ f_{n} & f_{n-1} \\ \end{pmatrix}^2$$

• $f_{a+b}=f_{a-1} \cdot f_b+f_a \cdot f_{b+1}$

• $f_{2n}=f_{n-1}f_n+f_nf_{n+1}$

• $f_1+f_3+\dots +f_{2n-1} = f_{2n},f_2 + f_4 + \dots + f_{2n} = f_{2n + 1} - 1$

• $\sum_{i=1}^n f_i = f_{n+2} - 1$

• $\sum_{i=1}^n f_i^2 = f_n \cdot f_{n+1}$

• $f_n^2=(-1)^{n-1} + f_{n-1} \cdot f_{n+1}$

• $gcd(f_a, f_b)=f_{gcd(a, b)}$

• 模 $n$ 周期（皮萨诺周期）

  • $\pi(p^k) = p^{k-1} \pi(p)$
  • $\pi(nm) = lcm(\pi(n), \pi(m)), \forall n \perp m$
  • $\pi(2)=3, \pi(5)=20$
  • $\forall p \equiv \pm 1\pmod {10}, \pi(p)|p-1$
  • $\forall p \equiv \pm 2\pmod {5}, \pi(p)|2p+2$

常见生成函数

• $(1+ax)^n=\sum_{k=0}^n \binom {n}{k} a^kx^k$
• $\dfrac{1-x^{r+1}}{1-x}=\sum_{k=0}^nx^k$
• $\dfrac1{1-ax}=\sum_{k=0}^{\infty}a^kx^k$
• $\dfrac 1{(1-x)^2}=\sum_{k=0}^{\infty}(k+1)x^k$
• $\dfrac1{(1-x)^n}=\sum_{k=0}^{\infty} \binom{n+k-1}{k}x^k$
• $e^x=\sum_{k=0}^{\infty}\dfrac{x^k}{k!}$
• $\ln(1+x)=\sum_{k=0}^{\infty}\dfrac{(-1)^{k+1}}{k}x^k$

低阶等幂求和

• $\sum_{i=1}^{n} i^{1} = \frac{n(n+1)}{2} = \frac{1}{2}n^2 +\frac{1}{2} n$
• $\sum_{i=1}^{n} i^{2} = \frac{n(n+1)(2n+1)}{6} = \frac{1}{3}n^3 + \frac{1}{2}n^2 + \frac{1}{6}n$
• $\sum_{i=1}^{n} i^{3} = \left[\frac{n(n+1)}{2}\right]^{2} = \frac{1}{4}n^4 + \frac{1}{2}n^3 + \frac{1}{4}n^2$
• $\sum_{i=1}^{n} i^{4} = \frac{n(n+1)(2n+1)(3n^2+3n-1)}{30} = \frac{1}{5}n^5 + \frac{1}{2}n^4 + \frac{1}{3}n^3 - \frac{1}{30}n$
• $\sum_{i=1}^{n} i^{5} = \frac{n^{2}(n+1)^{2}(2n^2+2n-1)}{12} = \frac{1}{6}n^6 + \frac{1}{2}n^5 + \frac{5}{12}n^4 - \frac{1}{12}n^2$
• 高阶见第二类斯特林数

一些组合公式

• 错排公式：$D_1=0,D_2=1,D_n=(n-1)(D_{n-1} + D_{n-2})=n!(\frac 1{2!}-\frac 1{3!}+\dots + (-1)^n\frac 1{n!})=\lfloor \frac{n!}e + 0.5 \rfloor$
• 卡特兰数（$n$ 对括号合法方案数，$n$ 个结点二叉树个数，$n\times n$ 方格中对角线下方的单调路径数，凸 $n+2$ 边形的三角形划分数，$n$ 个元素的合法出栈序列数）：$C_n=\frac 1{n+1}\binom {2n}n=\frac{(2n)!}{(n+1)!n!}$

 

数据结构

 

数位dp

 

ll cal(ll x, int n, int lim, int lead, array<int, 10> b) {
	if (n == -1) {
		return 0;
	}
	if (!lim && !lead&&dp[n].count(b))return dp[n][b];
	ll ans = 0;
	int up = (lim ? a[n] : 9);
	for (int i = 0; i <= up; i++) {
		ll tmp = 0;
		for (int j = 0; j < i; j++)tmp += b[j];
		if (lim && (i == up)) {
			ans += tmp * (x%p[n] + 1);
		}
		else {
			ans += tmp * p[n];
		}
		if (!(lead && (i == 0)))b[i]++;
		ans += cal(x, n - 1, lim&(i == up), lead&(i == 0), b);
		if (!(lead && (i == 0)))b[i]--;
	}
	if (!lim && !lead)dp[n][b] = ans;
	return ans;
}

 

离散化

 

vector<int>vc;
int init() {
	for (int i = 1; i <= n; i++) {
		vc.push_back(lap[i].w);
	}
	sort(vc.begin(), vc.end());
  //vc.erase(unique(vc.begin(),vc.end()),vc.end());
	int t = unique(vc.begin(), vc.end()) - vc.begin();
	for (int i = 1; i <= t; i++) {
		lap[i].w = lower_bound(vc.begin(), vc.end(), lap[i].w) - vc.begin();
	}
	return t;
}

 

ST表

 

int mx[N][25];
void ini(int n) {
	for (int i = 1; i < 25; i++) {	//1e7
		for (int j = 1; j + (1 << i) - 1 <= n; j++) {
			mx[j][i] = max(mx[j][i - 1], mx[j + (1 << (i - 1))][i - 1]);
		}
	}
}
int rmq(int a, int b) {
	int len = log2(b - a + 1);
	return max(mx[a][len], mx[b - (1 << len) + 1][len]);
}

 

树状数组

 

int sum[N];//从1开始
int lowbit(int x) {
	return x & -x;
}
void add(int x) {
	for (int i = x; i <= n; i+=lowbit(i)) {
		sum[i]++;
	}
}
int query(int r) {
	int ans = 0;
	for (int i = r; i > 0; i -= lowbit(i)) {
		ans += sum[i];
	}
	return ans;
}

 

线段树

 以区间和为例

 

void push_up(int root)//根节点状态更新
{
    num[root] = num[root*2] + num[root*2+1];//区间和
}
void build(int l,int r,int root)//线段树建树
{
    if(l == r)
    {
        num[root]=a[l];
        return;
    }
    int mid = (l+r)/2;
    build(l,mid,root*2);
    build(mid+1,r,root*2+1);
    push_up(root);
}
inline void add(int i,int dis,int k){
    if(tree[i].l==tree[i].r){//如果是叶子节点，那么说明找到了
        tree[i].sum+=k;
        return ;
    }
    if(dis<=tree[i*2].r)  add(i*2,dis,k);//在哪往哪跑
    else  add(i*2+1,dis,k);
    tree[i].sum=tree[i*2].sum+tree[i*2+1].sum;//返回更新
    return ;
}
int query(int la,int rb,int l,int r,int root)//查询区间[la,rb]的值
{
    if(l>=la && r<=rb)
    {
        return num[root];
    }
    
    push_down(root,r-l+1);
    
    int mid = (l+r)/2;
    int ans=0;
    if(la<=mid)
    {
        ans += query(la,rb,l,mid,root*2);//区间和
    }
    if(rb>mid)
    {
        ans +=query(la,rb,mid+1,r,root*2+1);//区间和
    }
    
    return ans;
}

 

线段树（lazy）

 

//区间最小值
ll a[N];
ll tree[N << 2], laz[N << 2];
void pushup(int rt) {
	tree[rt] = min(tree[rt << 1], tree[(rt << 1) | 1]);
}
void build(int l, int r, int rt) {
	if (l == r) {
		tree[rt] = a[l];
		return;
	}
	build(lson);
	build(rson);
	pushup(rt);
}
void change(int x, int l, int r, int rt) {//单点修改
	if (l == r) {
		tree[rt] = INF;
		return;
	}
	if (x <= mid)change(x, lson);
	else change(x, rson);
	pushup(rt);
}
void pushdown(int rt) {
	ll& x = laz[rt];
	if (x) {
		tree[rt << 1] += x;
		tree[(rt << 1) | 1] += x;
		laz[rt << 1] += x;
		laz[(rt << 1) | 1] += x;
		x = 0;
	}
}
void update(int x, int ql, int qr, int l, int r, int rt) {//区间修改
	if (ql == l && qr == r) {
		laz[rt] += x;
		tree[rt] += x;
		return;
	}
	pushdown(rt);
	if (qr <= mid)update(x, ql, qr, lson);
	else if (ql > mid)update(x, ql, qr, rson);
	else {
		update(x, ql, mid, lson);
		update(x, mid + 1, qr, rson);
	}
	pushup(rt);
}
int query(int l, int r, int rt) {
	if (l == r)return l;
	pushdown(rt);
	if (tree[rson] == 0)return query(rson);
	else return query(lson);
}
int main(){
    build(1,n,1);
    //...
    return 0;
}

 

动态开点线段树

 

#define mid ((l+r)>>1)
#define lson l,mid,lc[rt]
#define rson mid+1,r,rc[rt]
int T[N], tr[N * 40], lc[N * 40], rc[N * 40], tot;
void up(int rt) {
	tr[rt] = tr[lc[rt]] + tr[rc[rt]];
}
void upd(int q, int x, int l, int r, int& rt) {
	if (!rt)rt = ++tot;
	if (l == r) {
		tr[rt] += x;
		return;
	}
	if (q <= mid)upd(q, x, lson);
	else upd(q, x, rson);
	up(rt);
}
int qry(int ql, int qr, int l, int r, int rt) {
	if (!rt)return 0;
	if (ql <= l && qr >= r)return tr[rt];
	int ans = 0;
	if (ql <= mid)ans += qry(ql, qr, lson);
	if (qr > mid)ans += qry(ql, qr, rson);
	return ans;
}

 

势能线段树

 

区间变max操作

#define mid ((l+r)>>1)
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
int trmn[N << 2], trsmn[N << 2], trcmn[N << 2], laz[N << 2];//区间最小，次小，最小值个数
int trsum[N << 2][30]; //对具体询问用，可改
void up(int rt) {
	if (trmn[rt << 1] == trmn[rt << 1 | 1]) {
		trmn[rt] = trmn[rt << 1];
		trcmn[rt] = trcmn[rt << 1] + trcmn[rt << 1 | 1];
		trsmn[rt] = min(trsmn[rt << 1], trsmn[rt << 1 | 1]);
	}
	else if (trmn[rt << 1] < trmn[rt << 1 | 1]) {
		trmn[rt] = trmn[rt << 1];
		trcmn[rt] = trcmn[rt << 1];
		trsmn[rt] = min(trsmn[rt << 1], trmn[rt << 1 | 1]);
	}
	else {
		trmn[rt] = trmn[rt << 1 | 1];
		trcmn[rt] = trcmn[rt << 1 | 1];
		trsmn[rt] = min(trsmn[rt << 1 | 1], trmn[rt << 1]);
	}
	for (int i = 0; i < 30; i++)trsum[rt][i] = trsum[rt << 1][i] + trsum[rt << 1 | 1][i];
}
void pushtag(int x, int l, int r, int rt) {
	if (x <= trmn[rt])return;
	for (int i = 0; i < 30; i++) {
		if (trmn[rt] >> i & 1)trsum[rt][i] -= trcmn[rt];
		if (x >> i & 1)trsum[rt][i] += trcmn[rt];
	}
	trmn[rt] = laz[rt] = x;
}
void down(int l, int r, int rt) {
	int& x = laz[rt];
	if (x) {
		pushtag(x, lson);
		pushtag(x, rson);
		x = 0;
	}
}
void build(int l, int r, int rt) {
	if (l == r) {
		trmn[rt] = a[l];
		trsmn[rt] = INF;
		trcmn[rt] = 1;
		for (int i = 0; i < 30; i++) {
			trsum[rt][i] = (a[l] >> i & 1);
		}
		return;
	}
	build(lson); build(rson);
	up(rt);
}
void upd(int ql, int qr, int x, int l, int r, int rt) {
	if (trmn[rt] >= x)return;
	if (ql <= l && qr >= r && trsmn[rt] > x) {
		pushtag(x, l, r, rt);
		return;
	}
	down(l, r, rt);
	if (ql <= mid)upd(ql, qr, x, lson);
	if (qr > mid)upd(ql, qr, x, rson);
	up(rt);
}
int cnt[30];
void qry(int ql, int qr, int l, int r, int rt) {
	if (ql <= l && qr >= r) {
		for (int i = 0; i < 30; i++)cnt[i] += trsum[rt][i];
		return;
	}
	down(l, r, rt);
	if (ql <= mid)qry(ql, qr, lson);
	if (qr > mid)qry(ql, qr, rson);
}

 

二维线段树（树套树）

（区间求max，无修改，可加单点修改）

快，空间大

#define mid ((l+r)>>1)
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
ll tr[N << 2][N << 2];
void up(int id, int rt) {
	while (id) {
		if (id >> 1)tr[id >> 1][rt] = max(tr[id >> 1][rt], tr[id][rt]);
		id >>= 1;
	}
}
void buildr(int q, int id, int l, int r, int rt) {
	if (l == r) {
		tr[id][rt] = a[q][l];
		up(id, rt);
		return;
	}
	buildr(q, id, lson);
	buildr(q, id, rson);
	tr[id][rt] = max(tr[id][rt << 1], tr[id][rt << 1 | 1]);
	up(id, rt);
}
inline void build(int l, int r, int rt) {
	if (l == r) {
		buildr(l, rt, 1, n, 1);
		return;
	}
	build(lson);
	build(rson);
}
ll qryr(int id, int ql, int qr, int l, int r, int rt) {
	if (ql <= l && qr >= r)return tr[id][rt];
	ll ans = 0;
	if (ql <= mid)ans = max(ans, qryr(id, ql, qr, lson));
	if (qr > mid && ans < tr[id][rt << 1 | 1])ans = max(ans, qryr(id, ql, qr, rson));
	return ans;
}
inline ll qry(int ql, int qr, int pl, int pr, int l, int r, int rt) {
	if (ql <= l && qr >= r)return qryr(rt, pl, pr, 1, n, 1);
	ll ans = 0;
	if (ql <= mid)ans = max(ans, qry(ql, qr, pl, pr, lson));
	if (qr > mid && ans < tr[rt << 1 | 1][1])ans = max(ans, qry(ql, qr, pl, pr, rson));
	return ans;
}

build(1, n, 1);
ans = qry(x1, x2, y1, y2, 1, n, 1)

慢，空间小

ll tr[N*N * 4];
void up(int rt) {
	tr[rt] = max(tr[rt << 1], tr[rt << 1 | 1]);
}
void build(int xl, int xr, int yl, int yr, int rt, int flg) {
	if (xl > xr || yl > yr)return;
	if (xl == xr && yl == yr) {
		tr[rt] = a[xl][yl];
		return;
	}
	if (flg) {
		int mid = ((xl + xr) >> 1);
		build(xl, mid, yl, yr, rt << 1, flg ^ 1);
		build(mid + 1, xr, yl, yr, rt << 1 | 1, flg ^ 1);
		up(rt);
	}
	else {
		int mid = ((yl + yr) >> 1);
		build(xl, xr, yl, mid, rt << 1, flg ^ 1);
		build(xl, xr, mid + 1, yr, rt << 1 | 1, flg ^ 1);
		up(rt);
	}
}
ll ans;
void qry(int qxl, int qxr, int qyl, int qyr, int xl, int xr, int yl, int yr, int rt, int flg) {
	if (qxl <= xl && qxr >= xr && qyl <= yl && qyr >= yr) {
		ans = max(ans, tr[rt]);
		return;
	}
	if (flg) {
		int mid = ((xl + xr) >> 1);
		if (qxl <= mid)qry(qxl, qxr, qyl, qyr, xl, mid, yl, yr, rt << 1, flg ^ 1);
		if (qxr > mid && ans < tr[rt << 1 | 1])qry(qxl, qxr, qyl, qyr, mid + 1, xr, yl, yr, rt << 1 | 1, flg ^ 1);
	}
	else {
		int mid = ((yl + yr) >> 1);
		if (qyl <= mid)qry(qxl, qxr, qyl, qyr, xl, xr, yl, mid, rt << 1, flg ^ 1);
		if (qyr > mid && ans < tr[rt << 1 | 1])qry(qxl, qxr, qyl, qyr, xl, xr, mid + 1, yr, rt << 1 | 1, flg ^ 1);
	}
}

build(1, n, 1, n, 1, 1);
ans = -INF;
qry(x1, x2, y1, y2, 1, n, 1, n, 1, 1);

 

主席树

 （第k大）

 

int a[N];
vector<int>vc;
int getid(int x) {//离散化
	return lower_bound(vc.begin(), vc.end(), x) - vc.begin() + 1;
}
int cnt, root[N];
struct node
{
	int l, r, sum;
}T[N*40];
void update(int l, int r, int &x, int y, int pos) {
	T[++cnt] = T[y];
	T[cnt].sum++;
	x = cnt;
	if (l == r)return;
	int mid = (l + r) >> 1;
	if (mid >= pos)update(l, mid, T[x].l, T[y].l, pos);
	else update(mid + 1, r, T[x].r, T[y].r, pos);
}
int query(int l, int r, int x, int y, int k) {
	if (l == r)return l;
	int mid = (l + r) >> 1;
	int sum = T[T[y].l].sum - T[T[x].l].sum;
	if (sum >= k)return query(l, mid, T[x].l, T[y].l, k);
	else return query(mid + 1, r, T[x].r, T[y].r, k - sum);
}
int main(){
    update(1,n,root[i],root[i-1],getid(a[i]));
    cout<<vc[query(1,n,L-1,R,k)];
}

 

带修改主席树

 

#include <algorithm>
#include <cstdio>
#include <cstring>
#include <map>
#include <set>
#define LC o << 1
#define RC o << 1 | 1
using namespace std;
const int maxn = 1000010;
int n, m, a[maxn], u[maxn], x[maxn], l[maxn], r[maxn], k[maxn], cur, cur1, cur2,
    q1[maxn], q2[maxn], v[maxn];
char op[maxn];
set<int> ST;
map<int, int> mp;
struct segment_tree  // 封装的动态开点权值线段树
{
  int cur, rt[maxn * 4], sum[maxn * 60], lc[maxn * 60], rc[maxn * 60];
  void build(int& o) { o = ++cur; }
  void print(int o, int l, int r) {
    if (!o) return;
    if (l == r && sum[o]) printf("%d ", l);
    int mid = (l + r) >> 1;
    print(lc[o], l, mid);
    print(rc[o], mid + 1, r);
  }
  void update(int& o, int l, int r, int x, int v) {
    if (!o) o = ++cur;
    sum[o] += v;
    if (l == r) return;
    int mid = (l + r) >> 1;
    if (x <= mid)
      update(lc[o], l, mid, x, v);
    else
      update(rc[o], mid + 1, r, x, v);
  }
} st;
//树状数组实现
inline int lowbit(int o) { return (o & (-o)); }
void upd(int o, int x, int v) {
  for (; o <= n; o += lowbit(o)) st.update(st.rt[o], 1, n, x, v);
}
void gtv(int o, int* A, int& p) {
  p = 0;
  for (; o; o -= lowbit(o)) A[++p] = st.rt[o];
}
int qry(int l, int r, int k) {
  if (l == r) return l;
  int mid = (l + r) >> 1, siz = 0;
  for (int i = 1; i <= cur1; i++) siz += st.sum[st.lc[q1[i]]];
  for (int i = 1; i <= cur2; i++) siz -= st.sum[st.lc[q2[i]]];
  // printf("j %d %d %d %d\n",cur1,cur2,siz,k);
  if (siz >= k) {
    for (int i = 1; i <= cur1; i++) q1[i] = st.lc[q1[i]];
    for (int i = 1; i <= cur2; i++) q2[i] = st.lc[q2[i]];
    return qry(l, mid, k);
  } else {
    for (int i = 1; i <= cur1; i++) q1[i] = st.rc[q1[i]];
    for (int i = 1; i <= cur2; i++) q2[i] = st.rc[q2[i]];
    return qry(mid + 1, r, k - siz);
  }
}
/*
线段树实现
void build(int o,int l,int r)
{
    st.build(st.rt[o]);
    if(l==r)return;
    int mid=(l+r)>>1;
    build(LC,l,mid);
    build(RC,mid+1,r);
}
void print(int o,int l,int r)
{
    printf("%d %d:",l,r);
    st.print(st.rt[o],1,n);
    printf("\n");
    if(l==r)return;
    int mid=(l+r)>>1;
    print(LC,l,mid);
    print(RC,mid+1,r);
}
void update(int o,int l,int r,int q,int x,int v)
{
    st.update(st.rt[o],1,n,x,v);
    if(l==r)return;
    int mid=(l+r)>>1;
    if(q<=mid)update(LC,l,mid,q,x,v);
    else update(RC,mid+1,r,q,x,v);
}
void getval(int o,int l,int r,int ql,int qr)
{
    if(l>qr||r<ql)return;
    if(ql<=l&&r<=qr){q[++cur]=st.rt[o];return;}
    int mid=(l+r)>>1;
    getval(LC,l,mid,ql,qr);
    getval(RC,mid+1,r,ql,qr);
}
int query(int l,int r,int k)
{
    if(l==r)return l;
    int mid=(l+r)>>1,siz=0;
    for(int i=1;i<=cur;i++)siz+=st.sum[st.lc[q[i]]];
    if(siz>=k)
    {
        for(int i=1;i<=cur;i++)q[i]=st.lc[q[i]];
        return query(l,mid,k);
    }
    else
    {
        for(int i=1;i<=cur;i++)q[i]=st.rc[q[i]];
        return query(mid+1,r,k-siz);
    }
}
*/
int main() {
  scanf("%d%d", &n, &m);
  for (int i = 1; i <= n; i++) scanf("%d", a + i), ST.insert(a[i]);
  for (int i = 1; i <= m; i++) {
    scanf(" %c", op + i);
    if (op[i] == 'C')
      scanf("%d%d", u + i, x + i), ST.insert(x[i]);
    else
      scanf("%d%d%d", l + i, r + i, k + i);
  }
  for (set<int>::iterator it = ST.begin(); it != ST.end(); it++)
    mp[*it] = ++cur, v[cur] = *it;
  for (int i = 1; i <= n; i++) a[i] = mp[a[i]];
  for (int i = 1; i <= m; i++)
    if (op[i] == 'C') x[i] = mp[x[i]];
  n += m;
  // build(1,1,n);
  for (int i = 1; i <= n; i++) upd(i, a[i], 1);
  // print(1,1,n);
  for (int i = 1; i <= m; i++) {
    if (op[i] == 'C') {
      upd(u[i], a[u[i]], -1);
      upd(u[i], x[i], 1);
      a[u[i]] = x[i];
    } else {
      gtv(r[i], q1, cur1);
      gtv(l[i] - 1, q2, cur2);
      printf("%d\n", v[qry(1, n, k[i])]);
    }
  }
  return 0;
}

 

划分树

 

#include<stdio.h>
#include<string.h>
#include<algorithm>
#define N 100010
using namespace std;
typedef long long LL;
int a[N];       //原数组
int sorted[N];  //排序好的数组
//是一棵树，但把同一层的放在一个数组里。
int num[20][N];   //num[i] 表示i前面有多少个点进入左孩子
int val[20][N];   //20层,每一层元素排放，0层就是原数组
void build(int l,int r,int ceng)
{
  if(l==r) return ;
  int mid=(l+r)/2,isame=mid-l+1;  //isame保存有多少和sorted[mid]一样大的数进入左孩子
  for(int i=l;i<=r;i++) if(val[ceng][i]<sorted[mid]) isame--;
  int ln=l,rn=mid+1;   //本结点两个孩子结点的开头，ln左
  for(int i=l;i<=r;i++)
  {
    if(i==l) num[ceng][i]=0;
    else num[ceng][i]=num[ceng][i-1];
    if(val[ceng][i]<sorted[mid] || val[ceng][i]==sorted[mid]&&isame>0)
    {
      val[ceng+1][ln++]=val[ceng][i];
      num[ceng][i]++;
      if(val[ceng][i]==sorted[mid]) isame--;
    }
    else
    {
      val[ceng+1][rn++]=val[ceng][i];
}
  }
  build(l,mid,ceng+1);
  build(mid+1,r,ceng+1);
}
int look(int ceng,int sl,int sr,int l,int r,int k)
{
  if(sl==sr) return val[ceng][sl];
  int ly;  //ly 表示l 前面有多少元素进入左孩子
  if(l==sl) ly=0;  //和左端点重合时
  else ly=num[ceng][l-1];
  int tolef=num[ceng][r]-ly;  //这一层l到r之间进入左子树的有tolef个
  if(tolef>=k)
  {
    return look(ceng+1,sl,(sl+sr)/2,sl+ly,sl+num[ceng][r]-1,k);
  }
  else
  {
    // l-sl 表示l前面有多少数，再减ly 表示这些数中去右子树的有多少个
    int lr = (sl+sr)/2 + 1 + (l-sl-ly);  //l-r 去右边的开头位置
    // r-l+1 表示l到r有多少数，减去去左边的，剩下是去右边的，去右边1个，下标就是lr，所以减1
    return look(ceng+1,(sl+sr)/2+1,sr,lr,lr+r-l+1-tolef-1,k-tolef);
  }
}
int main()
{
  int n,m,l,r,k;
  while(scanf("%d%d",&n,&m)!=EOF)
  {

    for(int i=1;i<=n;i++)
    {
      scanf("%d",&val[0][i]);
      sorted[i]=val[0][i];
    }
    sort(sorted+1,sorted+n+1);
    build(1,n,0);
    while(m--)
    {
      scanf("%d%d%d",&l,&r,&k);
      printf("%d\n",look(0,1,n,l,r,k));
    }
  }
  return 0;
}

 

Trie

int ins(char s[], ll v) {
	int rt = 0;
	for (int i = 0; s[i]; i++) {
		int bt = s[i] - '0';
		if (!ch[rt][bt]) {
			int u = st.top(); st.pop();
			ch[u][0] = ch[u][1] = 0;
			val[u] = 0;
			ch[rt][bt] = u;
		}
		rt = ch[rt][bt];
		val[rt] += v;
	}
	return rt;
}
int qry(char s[]) {
	int rt = 0;
	for (int i = 0; s[i]; i++) {
		int bt = s[i] - '0';
		if (!ch[rt][bt])return -1;
		rt = ch[rt][bt];
	}
	return rt;
}

 

可持久化Trie

 

struct perTrie {
    int tot, rt[N], ch[N * 33][2], sum[N * 33];

    void insert(int o, int lst, int v) {
        for (int i = 31; i >= 0; i--) {
            sum[o] = sum[lst] + 1;
            int c = ((v >> i) & 1);
            if (!ch[o][c])ch[o][c] = ++tot;
            ch[o][c ^ 1] = ch[lst][c ^ 1];
            o = ch[o][c];
            lst = ch[lst][c];
        }
        sum[o] = sum[lst] + 1;
    }
} T;

 

树上启发式合并

 

• 先算轻儿子，不保存统计数据
• 再算重儿子，保存统计数据
• 再算轻儿子，合并到统计数据中

void dfs2(int u, int _fa) {
	for (int v : G[u]) {
        if (v == _fa)continue;
		if (v == son[u])continue;
		dfs2(v);
		dfsdel(v);
	}
	if (son[u])dfs2(son[u]);
	for (int v : G[u]) {
        if (v == _fa)continue;
		if (v == son[u])continue;
		cal_ans();
		dfsadd(v);
	}
	add(u);
}

 

KD树

 

build $O(n\log n)$

query $O(n^{1-\frac{1}{k}})$

询问点坐标存在d[i]

原题：共3维，查询第3维小于等于询问点的条件下前2维id最小的最近点。

#define DIM 3
int d[DIM];
int cmp_d, root;
struct P
{
	int id; ll d[DIM], mx[DIM], mn[DIM]; int lc, rc;
}a[N];
bool cmp(P a, P b) {
	return a.d[cmp_d] < b.d[cmp_d];
}
void up(int u, int v) {
	for (int i = 0; i < DIM; i++) {
		a[u].mn[i] = min(a[u].mn[i], a[v].mn[i]);
		a[u].mx[i] = max(a[u].mx[i], a[v].mx[i]);
	}
}
int build(int l, int r, int D) {
	cmp_d = D;
	int mid = (l + r) / 2;
	nth_element(a + l + 1, a + mid + 1, a + r + 1, cmp);
	for (int i = 0; i < DIM; i++)a[mid].mn[i] = a[mid].mx[i] = a[mid].d[i];
	if (l != mid)a[mid].lc = build(l, mid - 1, (D + 1) % DIM);
	else a[mid].lc = 0;
	if (r != mid)a[mid].rc = build(mid + 1, r, (D + 1) % DIM);
	else a[mid].rc = 0;
	if (a[mid].lc)up(mid, a[mid].lc);
	if (a[mid].rc)up(mid, a[mid].rc);
	return mid;
}
int idx;
ll dis;
ll getdis(int p) {
	ll res = 0;
	if (a[p].mn[2] > d[2])return inf + 1;
	for (int i = 0; i < 2; i++) {
		if (d[i] < a[p].mn[i])res += (d[i] - a[p].mn[i])*(d[i] - a[p].mn[i]);
		if (d[i] > a[p].mx[i])res += (d[i] - a[p].mx[i])*(d[i] - a[p].mx[i]);
	}
	return res;
}
void qry(int p) {
	ll d0 = 0, dl = inf + 1, dr = inf + 1;
	if (a[p].d[2] <= d[2]) {
		for (int i = 0; i < 2; i++) {
			d0 += (d[i] - a[p].d[i])*(d[i] - a[p].d[i]);
		}
		if (d0 < dis) {
			dis = d0;
			idx = p;
		}
		else if (d0 == dis) {
			if (a[idx].id > a[p].id)idx = p;
		}
	}
	if (a[p].lc)dl = getdis(a[p].lc);
	if (a[p].rc)dr = getdis(a[p].rc);
	if (dl < dr) {
		if (dl <= dis)qry(a[p].lc);
		if (dr <= dis)qry(a[p].rc);
	}
	else {
		if (dr <= dis)qry(a[p].rc);
		if (dl <= dis)qry(a[p].lc);
	}
}

root = build(1, n, 0);
qry(root);

 

并查集

 

int par[N];
int rk[N];
void init(int n) {
    for (int i = 0; i < n; i++) {
        par[i] = i;
        rk[i] = 0;
    }
}
int find(int x) {
    if (par[x] == x) {
        return x;
    }
    else {
        return par[x] = find(par[x]);
    }
}
void unite(int x, int y) {
    x = find(x);
    y = find(y);
    if (x == y)return;
    if (rk[x] < rk[y]) {
        par[x] = y;
    }
    else {
        par[y] = x;
        if (rk[x] == rk[y])rk[x]++;
    }
}
bool same(int x, int y) {
    return find(x) == find(y);
}

 

LCT

 

路径异或值

#include <bits/stdc++.h>
using namespace std;
#define ll long long
const int INF = 0x3f3f3f3f;
const int N = 1e5 + 10;
int n, m;
struct LCT
{
	#define lc c[x][0]
	#define rc c[x][1]
	int v[N], s[N], f[N], c[N][2], siz[N];	//splay中的子树的siz
	bool r[N];//区间翻转
	inline bool nroot(int x) {
		return c[f[x]][0] == x || c[f[x]][1] == x;
	}
	inline void pushup(int x) {
		s[x] = s[lc] ^ s[rc] ^ v[x];
	}
	inline void rev(int x) { swap(lc, rc); r[x] ^= 1; }
	inline void pushdown(int x) {
		if (r[x]) {
			if (lc)rev(lc);
			if (rc)rev(rc);
			r[x] = 0;
		}
	}
	inline void update(int x) {
		siz[x] = siz[lc] + siz[rc];
	}
	inline void rotate(int x) {
		int y = f[x], z = f[y], k = c[y][1] == x, w = c[x][k ^ 1];
		if (nroot(y))c[z][c[z][1] == y] = x;
		if (w)f[w] = y;
		c[x][k ^ 1] = y; c[y][k] = w;
		f[y] = x; f[x] = z;
		pushup(y);
		update(y), update(x);//先更新y
	}
	inline void pushall(int x) {
		if (nroot(x))pushall(f[x]);
		pushdown(x);
	}
	inline void splay(int x) {	//使x作为其所在splay的根
		pushall(x);
		int y, z;
		while (nroot(x)) {
			y = f[x]; z = f[y];
			if (nroot(y))rotate((c[y][0] == x && c[z][0] == y ? y : x));
			rotate(x);
		}
		pushup(x);
	}
	inline void access(int x) {		//使根到x的路径独立成为一个splay
		for (int y = 0; x; y = x, x = f[x])
			splay(x), rc = y, pushup(x);
	}
	inline void makeroot(int x) {	//原树使成为根
		access(x); splay(x);
		rev(x);
	}
	int findroot(int x) {	//原树找根
		access(x); splay(x);
		while (lc)pushdown(x), x = lc;
		splay(x);
		return x;
	}
	inline void split(int x, int y) {	//使x到y的路径独立为一个splay
		makeroot(x);
		access(y); splay(y);
	}
	inline void link(int x, int y) {	//原树加边
		makeroot(x);
		if (findroot(y) != x)f[x] = y;
	}
	inline void cut(int x, int y) {		//原树删边
		makeroot(x);
		if (findroot(y) == x && f[y] == x && !c[y][0]) {
			f[y] = c[x][1] = 0;
			pushup(x);
		}
	}
}lct;


int main() {
	scanf("%d%d", &n, &m);
	for (int i = 1; i <= n; i++)scanf("%d", &lct.v[i]);
	while (m--) {
		int op, x, y;
		scanf("%d%d%d", &op, &x, &y);
		switch (op)
		{
		case 0:lct.split(x, y); printf("%d\n", lct.s[y]); break;
		case 1:lct.link(x, y); break;
		case 2:lct.cut(x, y); break;
		case 3:lct.splay(x); lct.v[x] = y; break;
		}
	}
	return 0;
}

 

舞蹈链

 

#include<cstdio>
#include<iostream>
#include<cstring>
#define clr(x) memset(x,0,sizeof(x))
#define clrlow(x) memset(x,-1,sizeof(x))
#define Node 1001010
#define N    1010
using namespace std;
struct DLX{
    int n,m; 
    int U[Node],D[Node],L[Node],R[Node],col[Node],row[Node];
    int H[N];
    int ansed,ans[N],size;
    void init(int _n,int _m)
    {
        n=_n;
        m=_m;
        for(int i=0;i<=m;i++)
        {
            U[i]=i;
            D[i]=i;
            L[i]=i-1;
            R[i]=i+1;
            col[i]=i;
            row[i]=0;
        }
        L[0]=m;
        R[m]=0;
        size=m;
        clrlow(H);
        clr(ans);
        ansed=0;
        return ;
    }
    void push(int r,int c)
    {
        size++;
        D[size]=D[c];
        U[size]=c;
        U[D[c]]=size;
        D[c]=size;
        row[size]=r;
        col[size]=c;
        if(H[r]<0)
        {
            H[r]=size;
            R[size]=L[size]=size;
        }
        else
        {
            L[size]=H[r];
            R[size]=R[H[r]];
            L[R[H[r]]]=size;
            R[H[r]]=size;
        }
    }
    void del(int c)
    {
        R[L[c]]=R[c];
        L[R[c]]=L[c];
        for(int i=D[c];i!=c;i=D[i])
            for(int j=R[i];j!=i;j=R[j])
            {
                D[U[j]]=D[j];
                U[D[j]]=U[j];
            }
        return ;
    }
    void reback(int c)
    {
        for(int i=U[c];i!=c;i=U[i])
            for(int j=L[i];j!=i;j=L[j])
            {
                D[U[j]]=j;
                U[D[j]]=j;
             } 
        R[L[c]]=c;
        L[R[c]]=c;
        return ;
    }
    bool dancing(int dep)
    {
        if(R[0]==0)
        {
            ansed=dep;
            return true;
        }
        int c=R[0];
        del(c);
        for(int i=D[c];i!=c;i=D[i])
        {
            ans[dep]=row[i];
            for(int j=R[i];j!=i;j=R[j])
                del(col[j]);
            if(dancing(dep+1))
                return true;
            for(int j=L[i];j!=i;j=L[j])
                reback(col[j]);
        }
        return false;
    }
}dlx;
int main()
{
    int n,m,p,k;
    while(scanf("%d%d",&n,&m)==2)
    {
        dlx.init(n,m);
        for(int i=1;i<=n;i++)
        {
            scanf("%d",&p);
            for(int j=1;j<=p;j++)
            {
                scanf("%d",&k);
                dlx.push(i,k);
            }    
        }
        if(!dlx.dancing(0))
            printf("NO\n");
            else
            {
                printf("%d",dlx.ansed);
                for(int i=0;i<dlx.ansed;i++)
                    printf(" %d",dlx.ans[i]);
                printf("\n");
            }
    }
    return 0;
 } 

 

无旋Treap

 

struct fhq_treap
{
	int tot;
	int tr[N][2], sz[N], val[N], rnd[N], min_[N], sum[N];
	void Init()
	{
		tot = 0;
		min_[0] = INF;
	}
	int newnode(int x) {
		++tot;
		sz[tot] = 1;
		sum[tot] = min_[tot] = val[tot] = x;
		tr[tot][0] = tr[tot][1] = 0;
		rnd[tot] = rand();
		return tot;
	}
	void up(int rt) {		//可改
		sz[rt] = 1 + sz[tr[rt][0]] + sz[tr[rt][1]];
		sum[rt] = val[rt] + sum[tr[rt][0]] + sum[tr[rt][1]];
		min_[rt] = min(val[rt], min(min_[tr[rt][0]], min_[tr[rt][1]]));
	}
	void split_by_sz(int now, int leftsz, int &x, int &y) {
		if (!now) { x = y = 0; return; }
		if (leftsz <= sz[tr[now][0]])y = now, split_by_sz(tr[now][0], leftsz, x, tr[now][0]);
		else x = now, split_by_sz(tr[now][1], leftsz - sz[tr[now][0]] - 1, tr[now][1], y);
		up(now);
	}
	void split_by_v(int now, int v, int &x, int &y) {	//第一棵树小于，第二棵大于等于
		if (!now) { x = y = 0; return; }
		if (!(val[now] >= v && min_[tr[now][1]] >= v))x = now, split_by_v(tr[now][1], v, tr[now][1], y);
		else y = now, split_by_v(tr[now][0], v, x, tr[now][0]);
		up(now);
	}
	int merge(int x, int y) {//注意这个操作的返回值是根节点
		if (!x || !y)return x + y;//如果有一棵树是空的，返回另一棵树就可以
		if (rnd[x] < rnd[y]) {//比较修正值
			tr[x][1] = merge(tr[x][1], y);//把y合并到x的右子树
			up(x);
			return x;
		}
		else {
			tr[y][0] = merge(x, tr[y][0]);//把x合并到y的左子树
			up(y);
			return y;
		}
	}
	void insert(int pos, int v, int &rt) {
		int x, y;
		split_by_sz(rt, pos - 1, x, y);
		rt = merge(merge(x, newnode(v)), y);
	}
	int kth(int now, int k) {
		if (k > sz[tr[now][0]] && k <= sz[now] - sz[tr[now][1]])return val[now];
		if (k <= sz[tr[now][0]])return kth(tr[now][0], k);
		else return kth(tr[now][1], k - (sz[now] - sz[tr[now][1]]));
	}
}Tr;

 

区间dp

 

int rela[N][N],dp[N];
//普通
for(int len = 1;len<=n;len++){//枚举长度
        for(int j = 1;j+len<=n+1;j++){//枚举起点，ends<=n
            int ends = j+len - 1;
            for(int i = j;i<ends;i++){//枚举分割点，更新小区间最优解
                dp[j][ends] = min(dp[j][ends],dp[j][i]+dp[i+1][ends]+something);
            }
        }
    }
//四边形优化
for (int len = 1; len <= n; len++) {//枚举长度
        for (int j = 1; j + len <= n + 1; j++) {//枚举起点，ends<=n
            int ends = j + len - 1;
            for (int k = rela[j][ends - 1]; k <= rela[j + 1][ends]; k++) {//枚举分割点，更新小区间最优解
                if (dp[j][ends] < dp[j][k] + dp[k + 1][ends] + 合并 {
                    dp[j][ends] = dp[j][k] + dp[k + 1][ends] + 合并;
                    rela[j][ends] = k;
                }
            }
        }
    }

 四边形优化

 s[i] [j-1]<=s[i] [j]<=s[i+1] [j]

 

单调栈

求不含坏点的矩形个数

int n, m;
int mz[N][N];
int a[N];
int st[N], tp;
int dp[N][N];

int main() {
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i++)for (int j = 1; j <= n; j++)mz[i][j] = 1;
    for (int i = 1; i <= m; i++) {
        int x, y;
        scanf("%d%d", &x, &y);
        mz[x][y] = 0;
    }
    ll ans = 0;
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= n; j++)
            if (!mz[i][j])a[j] = 0;
            else a[j]++;
        tp = 0;
        for (int j = 1; j <= n; j++) {
            while (tp && a[st[tp]] > a[j])tp--;
            if (tp)dp[i][j] = dp[i][st[tp]];
            dp[i][j] += (j - st[tp]) * a[j];
            ans += dp[i][j];
            st[++tp] = j;
        }
    }
    printf("%lld\n", ans);
    return 0;
}

 

图论

 

Tarjan求LCA

 

const int N = 5e5 + 7;
int n, m, u, v, s;
int tot = 0, st[N], to[N << 1], nx[N << 1], fa[N], ans[N], vis[N];
struct note { int node, id; }; //询问以结构体形式保存
vector<note> ques[N];

inline void add(int u, int v) { to[++tot] = v, nx[tot] = st[u], st[u] = tot; }
inline int getfa(int x) { return fa[x] == x ? x : fa[x] = getfa(fa[x]); } //并查集的getfa操作，路径压缩

void dfs(int u, int from)
{
    for (int i = st[u]; i; i = nx[i]) if (to[i] != from) dfs(to[i], u), fa[to[i]] = u; //将u的儿子合并到u
    int len = ques[u].size(); //处理与u有关的询问
    for (int i = 0; i < len; i++) if (vis[ques[u][i].node]) ans[ques[u][i].id] = getfa(ques[u][i].node); //对应的v已经访问并回溯时，LCA(u,v)就是v的fa里深度最小的一个也就是getfa(v)
    vis[u] = 1; //访问完毕回溯
}

int main()
{
    n = read(), m = read(), s = read();
    for (int i = 1; i < n; i++) u = read(), v = read(), add(u, v), add(v, u);
    for (int i = 1; i <= m; i++) u = read(), v = read(), ques[u].push_back((note){v, i}), ques[v].push_back((note){u, i}); //记下询问编号便于输出
    for (int i = 1; i <= n; i++) fa[i] = i;
    dfs(s, 0);
    for (int i = 1; i <= m; i++) printf("%d\n", ans[i]); //输出答案
    return 0;
}

 

求LCA

 

inline void dfs(int u,int fa)
{
    f[u][0]=fa;//2^0=1,所以f[u][0]存的是他的父亲节点
    depth[u]=depth[fa]+1;//叶子结点的深度比父亲节点大一
    for(re int i=1;(1<<i)<=depth[u];++i)f[u][i]=f[f[u][i-1]][i-1];//往上跳（倍增思想）
    for(re int i=head[u];i;i=edge[i].next)
    {
        int v=edge[i].to;
        if(v!=fa) dfs(v,u);
    }
}//建树
inline int lca(int u,int v)
{
    if(depth[u]<depth[v])swap(u,v);
    for(re int i=20;i>=0;--i)
    {
        if((1<<i)<=depth[u]-depth[v])
            u=f[u][i];
    }//u为深度较深的一点，先跳u使u，v达到同一深度
    if(u==v) return u;
    for(re int i=20;i>=0;--i)
    {
        if(f[u][i]!=f[v][i])
        {
            u=f[u][i];
            v=f[v][i];
        }
    }//达到同一深度后一起跳
    return f[u][0];
}
int main{
	dfs(1,0);
	cout<<lca(u,v);
}

 

int d[N];
int siz[N], fa[N], dep[N], son[N], topf[N], dfn[N], clk;
void dfs1(int u, int _fa) {
	siz[u] = 1; fa[u] = _fa;
	for (E e : G[u]) {
		int v = e.v;
		if (v == _fa)continue;
		dep[v] = dep[u] + 1;
		d[v] = d[u] + e.w;
		dfs1(v, u);
		siz[u] += siz[v];
		if (siz[v] > siz[son[u]])son[u] = v;
	}
}
void dfs2(int u, int topfa) {
	topf[u] = topfa;
	dfn[u] = ++clk;
	if (!son[u])return;
	dfs2(son[u], topfa);
	for (E e : G[u]) {
		if (!topf[e.v])dfs2(e.v, e.v);
	}
}
int LCA(int u, int v) {
	while (topf[u] ^ topf[v])
		dep[topf[u]] < dep[topf[v]] ? v = fa[topf[v]] : u = fa[topf[u]];
	return dep[u] < dep[v] ? u : v;
}
dfs1(1, 0);
dfs2(1, 1);

 

差分

 

二维差分

 

C[x1][y1] += x ,  C[x2 + 1][y2 + 1] += x ,  C[x1][y2 + 1] -= x , C[x2 + 1][y1] -= x;

前缀和

a[i][j] += a[i-1][j] + a[i][j-1] - a[i-1][j-1];
ans(x1,y1,x2,y2)=a[x2][y2]-a[x2][y1-1]-a[x1-1][y2]+a[x1-1][x2-1]

 

树上差分

 

 边差分：

 例如有一次操作是把红点（u）到绿点（v）之间的路径全部加x。那么我就标记dlt[u]+=x,dlt[v]+=x。然后我们要在lca(u,v)处标记dlt[lca(u,v)]-=2x。这样就使得加x的效果只局限在u…v，不会向lca(u,v)的爸爸蔓延。

 点差分：

 路径上所有点+=x

 dlt[u]+=x,dlt[v]+=x，把dlt[lca(u,v)]-=x并把dlt[fa[lca(u,v)]]-=x。

 

找环

 

包含双向环

void find_ring(int f,int u,int dep) {//父节点，当前，深度
	if (ans <= dep)return;
	if (vis[u]) { 
		ans = min(ans, dep);
		/*int t = dep;
		int tmp = u;
		while (t--) {
			cout << tmp << ' ';
			tmp = par[tmp];
		}
		cout << endl;*/
		return; 
	}
	vis[u] = 1;
	for (auto v : G[u]) {
		if (v == f)continue;
		par[v] = u;
		find_ring(u,v, dep + 1);
	}
	vis[u] = 0;
}

 

无双向环

自环，三元环，有问题

void dfs(int fa, int u) {
	vis[u] = 1;
	for (int i = 0; i < G[u].size(); i++) {
		int v = G[u][i].first;
		ll w = G[u][i].second;
		if (v == fa)continue;
		if (!vis[v]) {
			d[v] = d[u] ^ w;
			dfs(u, v);
		}
		else {
			//出现环
		}
	}
}

 

三元环计数

 

$\mathcal{O}(m\sqrt{m})$

#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
vector<int> g[N];
int deg[N], vis[N], n, m, ans;
struct E { int u, v; } e[N * 3];
int main() {
    scanf("%d%d", &n, &m);
    for(int i = 1 ; i <= m ; ++ i) {
        scanf("%d%d", &e[i].u, &e[i].v);
        ++ deg[e[i].u], ++ deg[e[i].v];
    }
    for(int i = 1 ; i <= m ; ++ i) {
        int u = e[i].u, v = e[i].v;
        if(deg[u] < deg[v] || (deg[u] == deg[v] && u > v)) swap(u, v);
        g[u].push_back(v);
    }
    for(int x = 1 ; x <= n ; ++ x) {
        for(auto y: g[x]) vis[y] = x;
        for(auto y: g[x])
            for(auto z: g[y])
                if(vis[z] == x)
                    ++ ans;
    }
    printf("%d\n", ans);
}

 

斯坦纳树

 

$dp[s][i]$ 代表与 $i$ 的联通情况为 $s$。

分两步转移：

1. 点内部转移。枚举 $s$ 的子集 $t$，$dp[s][i] = min(dp[s][i], dp[t][i] + dp[s\bigoplus t][i])$
2. 点之间转移。$dp[s][i]=min(dp[s][i],dp[s][j]+w[i][j])$，用dijkastra。

int dp[2020][110];
typedef pair<int, int>pii;
priority_queue<pii, vector<pii>, greater<pii> >q;
void dij(int* d) {
	while (!q.empty()) {
		int u = q.top().second, di = q.top().first; q.pop();
		if (di > d[u])continue;
		for (E& e : G[u]) {
			int v = e.v, w = e.w;
			if (d[v] > d[u] + w) {
				d[v] = d[u] + w;
				q.push({ d[v],v });
			}
		}
	}
}
for (int s = 0; s < (1 << k); s++) {
    for (int i = 1; i <= n; i++) {
        for (int t = (s - 1)&s; t; t = (t - 1)&s) {
            dp[s][i] = min(dp[s][i], dp[t][i] + dp[s^t][i]);
        }
        if (dp[s][i] != INF)q.push({ dp[s][i],i });
    }
    dij(dp[s]);
}
printf("%d\n", dp[(1 << k) - 1][x]);

 

SPFA

 

const int N = 1e5 + 10, maxm = 1e6 + 10;
int dis[N], tot[N];
bool inq[N];
vector<int>G[N];
struct E
{
	int u, v, w;
}edges[maxm];
void spfa(int s, int n) {
	memset(dis, 0x3f, sizeof(dis));
	queue<int> q;
	dis[s] = 0;
	q.push(s), inq[s] = true;
	while (!q.empty()) {
		int u = q.front();
		q.pop(), inq[u] = 0;
		for (int i : G[u]) {
			int v = edges[i].v, val = edges[i].w;
			if (dis[v] > dis[u] + val) {
				dis[v] = dis[u] + val;
				if (!inq[v]) q.push(v), tot[v]++, inq[v] = true;
				if (tot[v] > n) puts("-1"), exit(0);//负圈
			}
		}
	}
}

 

欧拉回路

 

Fluery

//需要提前确认存在欧拉回路
int S[N << 1], top;
Edge edges[N << 1];
set<int> G[N];

void DFS(int u) {
    S[top++] = u;
    for (int eid: G[u]) {
        int v = edges[eid].get_other(u);
        G[u].erase(eid);
        G[v].erase(eid);
        DFS(v);
        return;
    }
}

void fleury(int start) {
    int u = start;
    top = 0; path.clear();
    S[top++] = u;
    while (top) {
        u = S[--top];
        if (!G[u].empty())
            DFS(u);
        else path.push_back(u);
    }
}

 

DFS

//需要提前确认存在欧拉回路
int G[N][N];
void dfs(int u){
	for (int i = 1; i <= n; i++){
		if (G[i][u]){
			G[i][u]--, G[u][i]--;
			dfs(i);
			printf("%d %d\n", i, u);
		}
	}
}

 

最大流

 

struct mxfl
{
	int n = 0;
	int m = 0;
	int s, t;
	struct Edge
	{
		int from, to, cap, flow;
	};
	vector<Edge>edges;
	vector<int>G[N];
	void init(int _n, int _s, int _t) {
		n = _n;
		s = _s;
		t = _t;
		edges.clear();
		for (int i = 0; i < n; i++)G[i].clear();
	}
	void add_edge(int from, int to, int cap) {
		edges.push_back(Edge{ from,to,cap,0 });
		edges.push_back(Edge{ to,from,0,0 });
		m = (int)edges.size();
		G[from].push_back(m - 2);
		G[to].push_back(m - 1);
	}
	bool vis[N];
	int d[N], cur[N];
	bool bfs() {
		memset(vis, 0, sizeof(vis));
		queue<int>Q;
		Q.push(s);
		d[s] = 0;
		vis[s] = 1;
		while (!Q.empty()) {
			int x = Q.front(); Q.pop();
			for (int i = 0; i < (int)G[x].size(); i++) {
				Edge& e = edges[G[x][i]];
				if (!vis[e.to] && e.cap > e.flow) {
					vis[e.to] = 1;
					d[e.to] = d[x] + 1;
					Q.push(e.to);
				}
			}
		}
		return vis[t];
	}
	int dfs(int x, int a) {
		if (x == t || a == 0)return a;
		int flow = 0, f;
		for (int& i = cur[x]; i < (int)G[x].size(); i++) {
			Edge& e = edges[G[x][i]];
			if (d[x] + 1 == d[e.to] && (f = dfs(e.to, min(a, e.cap - e.flow))) > 0) {
				e.flow += f;
				edges[G[x][i] ^ 1].flow -= f;
				flow += f;
				a -= f;
				if (a == 0)break;
			}
		}
		return flow;
	}
	int maxflow() {
		int flow = 0;
		while (bfs()) {
			memset(cur, 0, sizeof(cur));
			flow += dfs(s, INF);
		}
		return flow;
	}
}MF;

 

最大流最小费用

 

struct E
{
	int from, to, cp, v;
	int rev;
	E() {}
	E(int f, int t, int cp, int v, int rev) :from(f), to(t), cp(cp), v(v), rev(rev) {}
};
struct MCMF
{
	int n, m, s, t;
	vector<E> edges;
	vector<int> G[N];
	bool inq[N];     //是否在队列
	int d[N];        //Bellman_ford单源最短路径
	int p[N];        //p[i]表从s到i的最小费用路径上的最后一条弧编号
	int a[N];        //a[i]表示从s到i的最小残量
	void init(int _n, int _s, int _t) {
		n = _n; s = _s; t = _t;
		for (int i = 0; i < n; i++) G[i].clear();
		edges.clear(); m = 0;
	}

	void addedge(int from, int to, int cap, int cost) {
		edges.push_back(E(from, to, cap, cost, 0));
		edges.push_back(E(to, from, 0, -cost, 1));
		G[from].push_back(m++);
		G[to].push_back(m++);
	}

	bool BellmanFord(int &flow, int &cost) {
		for (int i = 0; i < n; i++) d[i] = INF;
		memset(inq, 0, sizeof inq);
		d[s] = 0, a[s] = INF, inq[s] = true;
		queue<int> Q; Q.push(s);
		while (!Q.empty()) {
			int u = Q.front(); Q.pop();
			inq[u] = false;
			for (int& idx : G[u]) {
				E &e = edges[idx];
				if (e.cp && d[e.to] > d[u] + e.v) {
					d[e.to] = d[u] + e.v;
					p[e.to] = idx;
					a[e.to] = min(a[u], e.cp);
					if (!inq[e.to]) {
						Q.push(e.to);
						inq[e.to] = true;
					}
				}
			}
		}
		if (d[t] == INF) return false;
        //if (flow + a[t] > K)a[t] = K - flow;//固定流量
		flow += a[t];
		cost += a[t] * d[t];
		int u = t;
		while (u != s) {
			edges[p[u]].cp -= a[t];
			edges[p[u] ^ 1].cp += a[t];
			u = edges[p[u]].from;
		}
        //if (flow == K)return false;//固定流量
		return true;
	}

	pii go() {
		int flow = 0, cost = 0;
		while (BellmanFord(flow, cost));
		return pii(flow, cost);
	}
} MM;

 

二分图染色

 

int col[N];
vector<int>G[N];
bool bipar(int u) {	//1,2
	for (int v : G[u]) {
		if (col[v] == col[u])return false;
		if (!col[v]) {
			col[v] = 3 - col[u];
			if (!bipar(v))return false;
		}
	}
	return true;
}

 

二分图匹配（匈牙利）

 

点的序号一定要连续！！

不需要预先划分点集

int V;
vector<int>G[N];
int match[N];
bool used[N];
void add_edge(int u, int v) {
	G[u].push_back(v);
	G[v].push_back(u);
}
bool dfs(int v) {
	used[v] = 1;
	for (int i = 0; i < G[v].size(); i++) {
		int u = G[v][i], w = match[u];
		if (w < 0 || !used[w] && dfs(w)) {
			match[v] = u;
			match[u] = v;
			return true;
		}
	}
	return false;
}
int bi_match() {
	int res = 0;
	memset(match, -1, sizeof(match));
	for (int v = 1; v <= V; v++) {//改从1或0开始，到小于或等于V
		if (match[v] < 0) {
			memset(used, 0, sizeof(used));
			if (dfs(v)) {
				res++;
			}
		}
	}
	return res;
}

 

KM最大权完备匹配

 

$\mathcal{O}(n^3)$

int w[N][N];
int lx[N], ly[N];
int linker[N];
int slack[N];
int n;
bool visy[N];
int pre[N];
void bfs(int k) {
	int x, y = 0, yy = 0, delta;
	memset(pre, 0, sizeof(pre));
	for (int i = 1; i <= n; i++) slack[i] = INF;
	linker[y] = k;
	while (1) {
		x = linker[y]; delta = INF; visy[y] = true;
		for (int i = 1; i <= n; i++) {
			if (!visy[i]) {
				if (slack[i] > lx[x] + ly[i] - w[x][i]) {
					slack[i] = lx[x] + ly[i] - w[x][i];
					pre[i] = y;
				}
				if (slack[i] < delta) delta = slack[i], yy = i;
			}
		}
		for (int i = 0; i <= n; i++) {
			if (visy[i]) lx[linker[i]] -= delta, ly[i] += delta;
			else slack[i] -= delta;
		}
		y = yy;
		if (linker[y] == -1) break;
	}
	while (y) linker[y] = linker[pre[y]], y = pre[y];
}

int KM() {
	memset(lx, 0, sizeof(lx));
	memset(ly, 0, sizeof(ly));
	memset(linker, -1, sizeof(linker));
	for (int i = 1; i <= n; i++) {
		memset(visy, false, sizeof(visy));
		bfs(i);
	}
	int res = 0;
	for (int i = 1; i <= n; i++) {
		if (linker[i] != -1) {
			res += w[linker[i]][i];
		}
	}
	return res;
}

 

一般图匹配（带花树）

 

$\mathcal{O}(n^3)$

struct Edmond
{
	int pre[N], nxt[N], to[N], n, cnt;
	int mate[N], link[N], vis[N], fa[N];
	int que[N], hd, tl;
	int ss[N], tim;
	void init(int _n) {
		n = _n;
		fill(pre, pre + n + 1, 0);
		fill(nxt, nxt + n + 1, 0);
		fill(to, to + n + 1, 0);
		fill(mate, mate + n + 1, 0);
		fill(link, link + n + 1, 0);
		cnt = hd = tl = 0;
	}
	void addEdge(int x, int y) {
		nxt[cnt] = pre[x];
		to[pre[x] = cnt++] = y;
	}
	int Find(int x) { return fa[x] == x ? x : fa[x] = Find(fa[x]); }
	int LCA(int x, int y) {
		memset(ss, 0, sizeof(ss));
		tim = 0;
		++tim;
		while (ss[x] != tim) {
			if (x) { ss[x] = tim; x = Find(link[mate[x]]); }
			std::swap(x, y);
		}
		return x;
	}
	void Flower(int x, int y, int p) {
		while (Find(x) != p) {
			link[x] = y;
			fa[y = mate[x]] = fa[x] = p;
			if (vis[y] == 1) vis[que[tl++] = y] = 2;
			x = link[y];
		}
	}
	bool match(int x) {
		hd = tl = 0;
		for (int i = 1; i <= n; ++i) vis[fa[i] = i] = 0;
		vis[que[tl++] = x] = 2;
		while (hd < tl) {
			x = que[hd++];
			for (int i = pre[x]; i; i = nxt[i]) {
				int u = to[i];
				if (!vis[u]) {
					vis[u] = 1;
					link[u] = x;
					if (!mate[u]) {
						while (x) {
							x = mate[link[u]];
							mate[mate[u] = link[u]] = u;
							u = x;
						}
						return true;
					}
					else
						vis[que[tl++] = mate[u]] = 2;
				}
				else if (vis[u] == 2 && Find(u) != Find(x)) {
					int p = LCA(x, u);
					Flower(x, u, p);
					Flower(u, x, p);
				}
			}
		}
		return false;
	}
	int go() {
		int ans = 0;	//匹配数
		for (int i = 1; i <= n; i++) {
			if (!mate[i] && match(i))ans++;
		}
		return ans;
	}
}ED;

 

强连通分量缩点

 

int low[N], dfn[N], clk, B, bl[N];
vector<int> bcc[N];
void init() { B = clk = 0; memset(dfn, 0, sizeof dfn); }
void tarjan(int u) {
    static int st[N], p;
    static bool in[N];
    dfn[u] = low[u] = ++clk;
    st[p++] = u; in[u] = true;
    for (int& v: G[u]) {
        if (!dfn[v]) {
            tarjan(v);
            low[u] = min(low[u], low[v]);
        } else if (in[v]) low[u] = min(low[u], dfn[v]);
    }
    if (dfn[u] == low[u]) {
        while (1) {
            int x = st[--p]; in[x] = false;
            bl[x] = B; bcc[B].push_back(x);
            if (x == u) break;
        }
        ++B;
    }
}

 

点-双联通分量

 

vector<int>G[N];
void add_edge(int u, int v) {
	G[u].push_back(v);
	G[v].push_back(u);
}
struct edge
{
	int u, v;
};
int pre[N], iscut[N], bccno[N], dfs_clock, bcc_cnt;
vector<int>bcc[N];
stack<edge>S;
int dfs(int u, int fa) {
	int lowu = pre[u] = ++dfs_clock;
	int child = 0;
	for (int i = 0; i < (int)G[u].size(); i++) {
		int v = G[u][i];
		edge e = edge{ u,v };
		if (!pre[v]) {
			S.push(e);
			child++;
			int lowv = dfs(v, u);
			lowu = min(lowu, lowv);
			if (lowv >= pre[u]) {
				iscut[u] = true;
				bcc_cnt++; bcc[bcc_cnt].clear();
				for (;;) {
					edge x = S.top(); S.pop();
					if (bccno[x.u] != bcc_cnt) {
						bcc[bcc_cnt].push_back(x.u);
						bccno[x.u] = bcc_cnt;
					}
					if (bccno[x.v] != bcc_cnt) {
						bcc[bcc_cnt].push_back(x.v);
						bccno[x.v] = bcc_cnt;
					}
					if (x.u == u && x.v == v)break;
				}
			}
		}
		else if (pre[v] < pre[u] && v != fa) {
			S.push(e);
			lowu = min(lowu, pre[v]);
		}
	}
	if (fa < 0 && child == 1)iscut[u] = 0;
	return lowu;
}
void find_bcc(int n) {
	memset(pre, 0, sizeof(pre));
	memset(iscut, 0, sizeof(iscut));
	memset(bccno, 0, sizeof(bccno));
	dfs_clock = bcc_cnt = 0;
	for (int i = 1; i <= n; i++) {
		if (!pre[i])dfs(i, -1);
	}
}

 

桥

 

int dfn[N], low[N], clk;
void init() { memset(dfn, 0, sizeof dfn); clk = 0; }
void tarjan(int u, int fa) {
    low[u] = dfn[u] = ++clk;
    int _fst = 0;
    for (E& e: G[u]) {
        int v = e.to; if (v == fa && ++_fst == 1) continue;
        if (!dfn[v]) {
            tarjan(v, u);
            if (low[v] > dfn[u]) // ...有桥e
            low[u] = min(low[u], low[v]);
        } else low[u] = min(low[u], dfn[v]);
    }
}

 

边双缩点

 

int dfn[N], low[N], clk;
int S[N], top, cc[N], cnt;
void tarjan(int u, int fa) {
	low[u] = dfn[u] = ++clk;
	int _fst = 0;
	S[top++] = u;
	for (int v : G[u]) {
		if (v == fa && ++_fst == 1) continue;//可能有重边
		if (!dfn[v]) {
			tarjan(v, u);
			low[u] = min(low[u], low[v]);
		}
		else low[u] = min(low[u], dfn[v]);
	}
	if (low[u] == dfn[u]) {
		cnt++;
		int tmp;
		do {
			tmp = S[--top];
			cc[tmp] = cnt;
		} while (tmp != u);
	}
}

 

2-sat

 

$\mathcal{O}(n\cdot m)$

struct Twosat
{
	int n;
	vector<int>G[N<<1];
	bool mark[N << 1];
	int S[N << 1], c;
	bool dfs(int x) {
		if (mark[x ^ 1])return false;
		if (mark[x])return true;
		mark[x] = true;
		S[c++] = x;
		for (int i = 0; i < G[x].size(); i++) {
			if (!dfs(G[x][i]))return false;
		}
		return true;
	}
	void init(int n) {
		this->n = n;
		for (int i = 0; i < n * 2; i++)G[i].clear();
		memset(mark, 0, sizeof(mark));
	}
	//x=xval or y=yval
	void add_clause(int x, int xval, int y, int yval) {
		x = x * 2 + xval;
		y = y * 2 + yval;
		G[x ^ 1].push_back(y);
		G[y ^ 1].push_back(x);
	}
	bool solve() {
		for (int i = 0; i < n * 2; i += 2) {
			if (!mark[i] && !mark[i ^ 1]) {
				c = 0;
				if (!dfs(i)) {
					while (c > 0)mark[S[--c]] = false;
					if (!dfs(i ^ 1))return false;
				}
			}
		}
		return true;
	}
};

 

$\mathcal{O}(n+m)$ 随机答案

1. 使用tarjan缩点，那么一个强连通分量里的点选一则必须选全部
2. 做一次检查，如果有一对点在同一个强连通分量里，输出无解信息。
3. Tarjan得到scc序为拓扑序反序，一对点中取真实拓扑序小的，即scc序大的。

int n, m;
vector<int>G[N << 1];
int dfn[N << 1], low[N << 1], ins[N << 1], dfsClock;
int sccCnt, color[N << 1];
stack<int>stk;
// 注意所有东西都要开两倍空间，因为每个变量存了两次
void tarjan(int u) {
	low[u] = dfn[u] = ++dfsClock;
	stk.push(u); ins[u] = true;
	for (int i = 0; i < (int)G[u].size();i++) {
		int v = G[u][i];
		if (!dfn[v]) tarjan(v), low[u] = min(low[u], low[v]);
		else if (ins[v]) low[u] = min(low[u], dfn[v]);
	}
	if (low[u] == dfn[u]) {
		++sccCnt;
		do {
			color[u] = sccCnt;
			u = stk.top(); stk.pop(); ins[u] = false;
		} while (low[u] != dfn[u]);
	}
}
void solve() {
	// 使用了 Tarjan 找环，得到的 color[x] 是 x 所在的 scc 的拓扑逆序。
	for (int i = 1; i <= (n << 1); ++i) if (!dfn[i]) tarjan(i);
	for (int i = 1; i <= n; ++i)
		if (color[i] == color[i + n]) { // x 与 -x 在同一强连通分量内，一定无解
			puts("IMPOSSIBLE");
			exit(0);
		}
	puts("POSSIBLE");
	for (int i = 1; i <= n; ++i)
		printf("%d ", color[i] > color[i + n] ? 0 : 1); // 如果不使用 Tarjan 找环，改成小于号
	puts("");
}
int main() {
	scanf("%d%d", &n, &m);
	for (int i = 0; i < m; ++i) {
		int a, va, b, vb;
		scanf("%d%d%d%d", &a, &va, &b, &vb);//a=va||b=vb
		G[a + n * (va & 1)].push_back(b + n * (vb ^ 1));
		G[b + n * (vb & 1)].push_back(a + n * (va ^ 1));
	}
	solve();
	return 0;
}

 

拓扑排序

 

DFS

#include <iostream>
#include <stack>
using namespace std;

struct Edge {
    int to, next;
};

const int N = 10010;
int head[N] = {};
int n, m, cnt = 1;
bool vis[N] = {};
Edge edge[N];
stack<int> S;

void add(int u, int v)
{
    edge[cnt].to = v;
    edge[cnt].next = head[u];
    head[u] = cnt++;
}

void dfs(int u)
{
    vis[u] = true;
    for (int i = head[u]; i; i = edge[i].next) {
        int v = edge[i].to;
        if (!vis[v]) dfs(v);
    }
    S.push(u);
}

int main()
{
    cin >> n >> m;
    for (int i = 1; i <= m; ++i) {
        int u, v;
        cin >> u >> v;
        add(u, v);
    }
    for (int i = 1; i <= n; ++i) {
        if (vis[i] == 0) dfs(i);
    }
    while (!S.empty()) {
        cout << S.top() << ' ';
        S.pop();
    }
}

DFS判环

bool dfs(int u)
{
    vis[u] = 1;
    for (int i = head[u]; i; i = edge[i].next) {
        int v = edge[i].to;
        if (vis[v] == 1) return false;
        if (vis[v] == 0 && !dfs(v)) return false;
    }
    vis[u] = -1;
    S.push(u);
    return true;
}

 

Kahn算法

#include <bits/stdc++.h>
using namespace std;
const int N = 505;
struct node
{
	int v, next;
}edge[N*N];
int degree[N], head[N];
queue<int> q;
list<int> ans; 
int n, m, no;
inline void init()
{
	no = 0;
	while(!q.empty()) q.pop();
	memset(degree, 0, sizeof degree);
	memset(head, -1, sizeof head);
}
inline void add(int u, int v)
{
	edge[no].v = v;
	edge[no].next = head[u];
	head[u] = no++;
}
int Kahn()
{
	int count = 0;
	while(!q.empty())
	{
		int tp = q.front(); q.pop();
		++count; ans.push_back(tp);	//加入链表中，加入数组或者vector或者queue都无所谓 
		int k = head[tp];
		while(k != -1)
		{
			--degree[edge[k].v];
			if(!degree[edge[k].v]) q.push(edge[k].v);
			k = edge[k].next;
		}
	}
	if(count == n) return 1;
	return 0;
}
int main()
{
	int u, v;
	scanf("%d %d", &n, &m); init();
	for(int i = 1; i <= m; ++i)
	{
		scanf("%d %d", &u, &v);
		add(u, v); ++degree[v];
	}
	for(int i = 1; i <= n; ++i)
	{
		if(!degree[i]) q.push(i);
	}
	Kahn();
	list<int>::iterator it;
	for(it = ans.begin(); it != ans.end(); ++it)
	{
		cout << *it << " ";
	}
	cout << endl;
	return 0;
}

 

树上点分治

 

计算树上路径长度小于等于 x 的点对个数

bool vis[N];
int siz[N];
ll ans;
int get_sz(int u, int _fa){
    siz[u] = 1;
    for(int v:G[u]){
        if(v==_fa||vis[v])continue;
        siz[u]+=get_sz(v, u);
    }
    return siz[u];
}
typedef pair<int,int>pii;
pii get_rt(int u, int _fa,int tot){
    pii res = pii(INF, -1);
    int s=1,m=0;
    for(int v:G[u]){
        if(v==_fa||vis[v])continue;
        res = min(res, get_rt(v, u, tot));
        m = max(m, siz[v]);
        s+=siz[v];
    }
    m = max(m, tot - s);
    res = min(res, pii(m, u));
    return res;
}
void enu_paths(int u, int _fa, int d, vector<int>& ds){
    ds.push_back(d);
    for(int v:G[u]){
        if(v==_fa||vis[v])continue;
        enu_paths(v, u, d+1, ds);
    }
}
ll count_pairs(vector<int>& ds, int K){
    ll res = 0;
    sort(ds.begin(), ds.end());
    int j = ds.size();
    for(int i=0;i<ds.size();i++){
        while(j > 0 && ds[i] + ds[j - 1] > K) --j;
        res += j - (j > i ? 1 : 0);
    }
    return res / 2;
}
void solve(int u, int K){
    get_sz(u, -1);
    int rt = get_rt(u, -1, siz[u]).second;
    vis[rt] = 1;
    for(int v:G[rt]){
        if(vis[v])continue;
        solve(v, K);
    }
    vector<int>ds;
    ds.push_back(0);
    for(int v:G[rt]){
        if(vis[v])continue;
        vector<int>tds;
        enu_paths(v, rt, 1, tds);
        ans-=count_pairs(tds, K);
        ds.insert(ds.end(),tds.begin(),tds.end());
    }
    ans+=count_pairs(ds, K);
    vis[rt]=0;
}
ll cal(int x){
    if(x<0)return 0;
    ans=0;
    solve(1, x);
    debug(ans)
    return ans;
}

 

树链剖分（以区间和为例）

 

const int N = 1e5 + 5;
int n, m, r, mod;
#define len (r-l+1)//注意括号
#define mid ((l+r)>>1)
#define lson rt<<1,l,mid
#define rson rt<<1|1,mid+1,r
int cnt;
int a[N << 2], laz[N << 2];
int wt[N], w[N];//wt[]为新点上值，w[]为旧点上值
int fa[N], dep[N], siz[N], son[N], top[N], id[N];
vector<int>G[N];
void add_edge(int u, int v) {
	G[u].push_back(v);
	G[v].push_back(u);
}
void pushdown(int rt, int lenn) {
	laz[2 * rt] += laz[rt];
	laz[2 * rt + 1] += laz[rt];
	a[2 * rt] += laz[rt] * (lenn - (lenn >> 1));
	a[2 * rt + 1] += laz[rt] * (lenn >> 1);
	a[2 * rt] %= mod;
	a[2 * rt + 1] %= mod;
	laz[rt] = 0;
}
void build(int rt, int l, int r) {
	if (l == r) {
		a[rt] = wt[l];
		if (a[rt] > mod)a[rt] %= mod;
		return;
	}
	build(lson);
	build(rson);
	a[rt] = (a[rt << 1] + a[rt << 1 | 1]) % mod;
}
int query(int rt, int l, int r, int ql, int qr) {
	if (ql <= l && qr >= r)return a[rt];
	if (laz[rt])pushdown(rt, len);
	int a = 0, b = 0;
	if (ql <= mid)a = query(lson, ql, qr);
	if (qr > mid)b = query(rson, ql, qr);
	return (a + b) % mod;
}
void update(int rt, int l, int r, int ql, int qr, int k) {
	if (ql <= l && qr >= r) {
		laz[rt] += k;
		a[rt] += k * len;
	}
	else {
		if (laz[rt])pushdown(rt, len);
		if (ql <= mid)update(lson, ql, qr, k);
		if (qr > mid)update(rson, ql, qr, k);
		a[rt] = (a[rt << 1] + a[rt << 1 | 1]) % mod;
	}
}
//--------------------------------------------------
int sum(int x, int y) {
	int ret = 0;
	while (top[x] != top[y]) {
		if (dep[top[x]] < dep[top[y]])swap(x, y);//把x点改为所在链顶端的深度更深的那个点
		ret += query(1, 1, n, id[top[x]], id[x]);
		ret %= mod;
		x = fa[top[x]];//把x跳到x所在链顶端的那个点的上面一个点
	}
	if (dep[x] > dep[y])swap(x, y);//把x变为深度浅的点
	ret += query(1, 1, n, id[x], id[y]);
	ret %= mod;
	return ret;
}
void updates(int x, int y, int k) {
	k %= mod;
	while (top[x] != top[y]) {
		if (dep[top[x]] < dep[top[y]])swap(x, y);
		update(1, 1, n, id[top[x]], id[x], k);
		x = fa[top[x]];
	}
	if (dep[x] > dep[y])swap(x, y);
	update(1, 1, n, id[x], id[y], k);
}
int qson(int x) {
	return query(1, 1, n, id[x], id[x] + siz[x] - 1);
}
void updson(int x, int k) {
	update(1, 1, n, id[x], id[x] + siz[x] - 1, k);
}
void dfs1(int u, int f, int deep) {
	fa[u] = f;
	dep[u] = deep;
	siz[u] = 1;
	for (int i = 0; i < G[u].size(); i++) {
		int v = G[u][i];
		if (v == f)continue;
		dfs1(v, u, deep + 1);
		siz[u] += siz[v];
		if (siz[v] > siz[son[u]])
			son[u] = v;
	}
}
void dfs2(int x, int t) {
	id[x] = ++cnt;
	wt[cnt] = w[x];//把每个点的初始值赋到新编号上来 
	top[x] = t;
	if (!son[x])return;
	dfs2(son[x], t);
	for (int i = 0; i < G[x].size(); i++) {
		int v = G[x][i];
		if (v == fa[x] || v == son[x])continue;
		dfs2(v, v);
	}
}
int main(){
    cnt = 0; dfs1(r, 0, 1);
	cnt = 0; dfs2(r, r);
	build(1, 1, n);
    //...
    return 0;
}

 

虚树

 

前置 LCA 带 dfn

$\mathcal{O}(k)$

bool cmp(int x, int y) { return dfn[x] < dfn[y]; }
int top, s[N];
struct E
{
	int v, w;
};
vector<E>g[N];
vector<int>vt;	//虚树上的点
void build(int* h,int k) {
	vt.clear();
	sort(h + 1, h + k + 1, cmp);
	s[top = 1] = 1; g[1].clear(); vt.push_back(1);
	for (int i = 1, l; i <= k; i++) {
		if (h[i] != 1) {
			l = LCA(h[i], s[top]);
			if (l != s[top]) {
				while (dfn[l] < dfn[s[top - 1]]) {
					g[s[top - 1]].push_back(E{ s[top],dep[s[top]] - dep[s[top - 1]] });
					g[s[top]].push_back(E{ s[top - 1],dep[s[top]] - dep[s[top - 1]] });
					top--;
				}
				if (dfn[l] > dfn[s[top - 1]]) {
					g[l].clear(); vt.push_back(l);
					g[l].push_back(E{ s[top],dep[s[top]] - dep[l] });
					g[s[top]].push_back(E{ l,dep[s[top]] - dep[l] });
					s[top] = l;
				}
				else {
					g[l].push_back(E{ s[top],dep[s[top]] - dep[l] });
					g[s[top]].push_back(E{ l,dep[s[top]] - dep[l] });
					top--;
				}
			}
			g[h[i]].clear(); vt.push_back(h[i]);
			s[++top] = h[i];
		}
	}
	for (int i = 1; i < top; i++) {
		g[s[i]].push_back(E{ s[i + 1],dep[s[i + 1]] - dep[s[i]] });
		g[s[i + 1]].push_back(E{ s[i],dep[s[i + 1]] - dep[s[i]] });
	}
}

 

圆方树

 

vector<edge>gg[N];	//原图
vector<edge>G[N];	//圆方树
int dfn[N<<1], low[N<<1], dep[N<<1], fa[N<<1];
int cnt;
void solve_cir(int u, int v, int w){
    //处理环
}
void Tar(int u, int _fa) {
	dfn[u] = low[u] = ++cnt;
	fa[u] = _fa; dep[u] = dep[_fa] + 1;
	for (int i = 0; i < (int)gg[u].size(); i++) {
		int v = gg[u][i].v, w = gg[u][i].w;
		if (v == _fa)continue;
		if (!dfn[v]) {
			dis[v] = dis[u] + w;
			Tar(v, u);
			low[u] = min(low[u], low[v]);
		}
		else low[u] = min(low[u], dfn[v]);//返祖边
		if (dfn[u] < low[v]) {	//树边
			add_edge(u, v, w);
		}
	}
	for (int i = 0; i < (int)gg[u].size(); i++) {
		int v = gg[u][i].v, w = gg[u][i].w;
		if (v == _fa)continue;
		if (fa[v] != u && dfn[u] < dfn[v]) {//u在最高点处理环
			solve_cir(u, v, w);
		}
	}
}
Tar(1, 0);

 

最小树形图

 

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int N = 1e5 + 10;
const int INF = 0x3f3f3f3f;
struct E
{
	int u, v, w;
}es[10010];
int n, m, rt, mn[N], fa[N], tp[N], lp[N], tot, ans;
int zl() {
	while (1) {
		for (int i = 1; i <= n; i++)mn[i] = INF, fa[i] = tp[i] = lp[i] = 0;
		for (int i = 1, v, w; i <= m; i++)
			if (es[i].u != es[i].v && (w = es[i].w) < mn[v = es[i].v])
				mn[v] = w, fa[v] = es[i].u;
		mn[rt] = 0;
		for (int u = 1; u <= n; u++) {
			ans += mn[u];
			if (mn[u] == INF)return -1;
		}
		for (int u = 1, v = 1; u <= n; u++, v = u) {
			while (v != rt && tp[v] != u && !lp[v])tp[v] = u, v = fa[v];
			if (v != rt && !lp[v]) {
				lp[v] = ++tot;
				for (int k = fa[v]; k != v; k = fa[k])lp[k] = tot;
			}
		}
		if (!tot)return ans;
		for (int i = 1; i <= n; i++)if (!lp[i])lp[i] = ++tot;
		for (int i = 1; i <= m; i++)
			es[i].w -= mn[es[i].v], es[i].u = lp[es[i].u], es[i].v = lp[es[i].v];
		n = tot, rt = lp[rt], tot = 0;
	}
}
int main() {
	scanf("%d%d%d", &n, &m, &rt);
	for (int i = 1; i <= m; i++)
		scanf("%d%d%d", &es[i].u, &es[i].v, &es[i].w);
	printf("%d\n", zl());
	return 0;
}

 

矩阵树定理

 

求无向图的生成树个数

$L(G)=D(G)-A(G)$

$D(G)$ 为度数矩阵，仅对角线有值。$A(G)$ 为邻接矩阵，$A_{ij}$ 为 $i$ 与 $j$ 有几条连边。

生成树个数 = $L(G)$ 去掉任意第 $i$ 行 第 $i$ 列 后的行列式。

ll K[110][110];
void add(int x, int y) {
    K[x][x]++;
    K[y][y]++;
    K[x][y]--;
    K[y][x]--;
}
ll gauss(int n) {
    ll res = 1ll;
    for (int i = 1; i <= n - 1; i++) {
        for (int j = i + 1; j <= n - 1; j++) {
            while (K[j][i]) {
                int t = K[i][i] / K[j][i];
                for (int k = i; k <= n - 1; k++)
                    K[i][k] = (K[i][k] - t * K[j][k] % mod + mod) % mod;
                swap(K[i], K[j]);
                res = -res;
            }
        }
        res = (res*K[i][i]) % mod;
    }
    return (res + mod) % mod;
}

 

字符串

 

字符串哈希

 

ll h1[N], p1[N], h2[N], p2[N];
ll m1 = 998244353, m2 = 1e9 + 7;
ll P1 = 233, P2 = 3993;
void init(ll h[], ll p[], ll P, ll mod) {	//从1开始
    p[0] = 1;
    for (int i = 1; i <= n; i++) {
        h[i] = (h[i - 1] * P % mod + s[i] - 'a' + 1) % mod;
        p[i] = p[i - 1] * P % mod;
    }
}
ll hsh(int l, int r, ll h[], ll p[], ll mod) {
    return (h[r] - h[l - 1] * p[r - l + 1]%mod+mod)%mod;
}
ll hsh(int l, int r) {
    return hsh(l, r, h1, p1, m1) * 2000000000ll + hsh(l, r, h2, p2, m2);
}

 

KMP

 

int nxt[N];
void getNextVal(char* p) {//长度为i的p的前缀的最长公共前后缀
	int n = strlen(p);
	nxt[0] = -1; nxt[1] = 0;
	for (int i = 2; i <= n; i++) {
		int j = nxt[i - 1];
		while (j != -1 && p[i - 1] != p[j]) j = nxt[j];
		nxt[i] = j + 1;
	}
}
int kmp(char* s,char* p) { //总串s，模式串p
	int i = 0, j = 0;
	getNextVal(p);
	int slen = strlen(s);
	int plen = strlen(p);
	while (i < slen&&j<plen) {
		if (j == -1 || s[i] == p[j]) {
			i++;
			j++;
		}
		else {
			j = nxt[j];
		}
	}
	if (j == plen) {
		return i - j;
	}
	else return -1;
}

 

KMP自动机

 

int fail[N], trans[N][30]; //fail即KMP中nxt，trans表示从第i位经过字符j转移到的位置

void build(char *s) {	// s从1开始
    int n = strlen(s + 1);
    fail[0] = 0, fail[1] = 0;
    trans[0][s[1] - 'a'] = 1, trans[1][s[2] - 'a'] = 2;
    for (int i = 2, j = 0; i <= n; i++) {
        while (j && s[j + 1] != s[i])j = fail[j];
        fail[i] = j = (s[j + 1] == s[i] ? j + 1 : j);
        if (i < n)trans[i][s[i + 1] - 'a'] = i + 1;
    }
    for (int i = 0; i <= n; i++) {
        for (int j = 0; j < 26; j++) {
            if (!trans[i][j])trans[i][j] = trans[fail[i]][j];
        }
    }
}

 

扩展KMP

 

int nxt[N], ex[N];
void get_nxt(char* p) {//p的所有后缀与p的最长公共前缀的长度
	int len = strlen(p), i = 0, p0 = 1;
	nxt[0] = len;
	while (i + 1 < len&&p[i] == p[i + 1])i++;
	nxt[1] = i;
	for (i = 2; i < len; i++) {
		if (i + nxt[i - p0] < p0 + nxt[p0])nxt[i] = nxt[i - p0];
		else {
			int j = max(0, nxt[p0] + p0 - i);
			while (i + j < len&&p[i + j] == p[j])j++;
			nxt[i] = j;
			p0 = i;
		}
	}
}
void get_exkmp(char * s, char* p) {//s的所有后缀与p的最长公共前缀的长度
	int i = 0, j, p0, len = strlen(s), len2 = strlen(p);
	get_nxt(p);
	while (i < len2&&i < len&&s[i] == p[i])i++;
	ex[0] = i;
	p0 = 1;
	for (i = 1; i < len; i++) {
		if (nxt[i - p0] + i < ex[p0] + p0)ex[i] = nxt[i - p0];
		else {
			j = max(0, ex[p0] + p0 - i);
			while (i + j < len&&j < len2&&s[i + j] == p[j])j++;
			ex[i] = j;
			p0 = i;
		}
	}
}

 

Manacher

 

char Ma[N * 2];
int Mp[N * 2];//每一个中心的最长回文半径
void Manacher(char s[], int len) {
	int l = 0;
	Ma[l++] = '$';
	Ma[l++] = '#';
	for (int i = 0; i < len; i++) {
		Ma[l++] = s[i];
		Ma[l++] = '#';
	}
	Ma[l] = 0;
	int mx = 0, id = 0;
	for (int i = 0; i < l; i++) {
		Mp[i] = mx > i ? min(Mp[2 * id - i], mx - i) : 1;
		while (Ma[i + Mp[i]] == Ma[i - Mp[i]])Mp[i]++;
		if (i + Mp[i] > mx) {
			mx = i + Mp[i];
			id = i;
		}
	}
}

 

AC自动机

 

#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 6;
int n;

namespace AC {
int tr[N][26], tot;
int e[N], fail[N], lst[N];
void insert(char *s) {
  int u = 0;
  for (int i = 1; s[i]; i++) {
    if (!tr[u][s[i] - 'a']) tr[u][s[i] - 'a'] = ++tot;
    u = tr[u][s[i] - 'a'];
  }
  e[u]++;
}
queue<int> q;
void build() {
  for (int i = 0; i < 26; i++)
    if (tr[0][i]) q.push(tr[0][i]);
  while (q.size()) {
    int u = q.front();
    q.pop();
    for (int i = 0; i < 26; i++) {
      if (tr[u][i]){
          fail[tr[u][i]] = tr[fail[u]][i], q.push(tr[u][i]);
          lst[tr[u][i]] = (e[fail[tr[u][i]]] != inf ? fail[tr[u][i]] : lst[fail[tr[u][i]]]);	//lst指向存储了完整串的fail节点
      }
      else
        tr[u][i] = tr[fail[u]][i];
    }
  }
}
int query(char *t) {
  int u = 0, res = 0;
  for (int i = 1; t[i]; i++) {
    u = tr[u][t[i] - 'a'];  // 转移
    for (int j = u; j && e[j] != -1; j = fail[j]) {	//原题要求不同的模式串，所以遇过的直接退出
      res += e[j], e[j] = -1;						//e[j]=-1
    }
  }
  return res;
}
}  // namespace AC

char s[N];
int main() {//求有多少个模式串在文本串里出现过
  scanf("%d", &n);
  for (int i = 1; i <= n; i++) scanf("%s", s + 1), AC::insert(s);//模式串
  scanf("%s", s + 1);//文本串
  AC::build();
  printf("%d", AC::query(s));
  return 0;
}

 

后缀数组

 

int rk[N], sa[N], tmp[N], lcp[N], tk, n;	//0开始
bool compare_sa(int i, int j) {
	if (rk[i] != rk[j])return rk[i] < rk[j];
	else {
		int ri = i + tk <= n ? rk[i + tk] : -1;
		int rj = j + tk <= n ? rk[j + tk] : -1;
		return ri < rj;
	}
}
void constract_sa(const char* S) {
	int n = strlen(S);
	for (int i = 0; i <= n; i++) {
		sa[i] = i;
		rk[i] = i < n ? S[i] : -1;
	}
	for (tk = 1; tk <= n; tk *= 2) {
		sort(sa, sa + n + 1, compare_sa);
		tmp[sa[0]] = 0;
		for (int i = 1; i <= n; i++) {
			tmp[sa[i]] = tmp[sa[i - 1]] + (compare_sa(sa[i - 1], sa[i]) ? 1 : 0);
		}
		for (int i = 0; i <= n; i++) {
			rk[i] = tmp[i];
		}
	}
}
void constract_lcp(const char* S) {
	int n = strlen(S);
	for (int i = 0; i <= n; i++) {
		rk[sa[i]] = i;
	}
	int h = 0;
	lcp[1] = 0;
	for (int i = 0; i < n; i++) {
		int j = sa[rk[i] - 1];
		if (h > 0)h--;
		for (; j + h < n&&i + h < n; h++) {
			if (S[j + h] != S[i + h])break;
		}
		lcp[rk[i]] = h;
	}
}

 

更快的奇妙写法

int wa[N], wb[N], wv[N], wts[N];	//0开始
int cmp(int *r, int a, int b, int l) {
	return r[a] == r[b] && r[a + l] == r[b + l];
}
void init_sa(char *r, int *sa, int n, int m) {
	int i, j, *x = wa, *y = wb, *t;
	int p;
	for (i = 0; i < m; i++) wts[i] = 0;
	for (i = 0; i < n; i++) wts[x[i] = r[i]]++;
	for (i = 0; i < m; i++) wts[i] += wts[i - 1];
	for (i = n - 1; i >= 0; --i) sa[--wts[x[i]]] = i;
	for (j = 1, p = 1; p < n; j <<= 1, m = p) {
		for (p = 0, i = n - j; i < n; i++) y[p++] = i;
		for (i = 0; i < n; i++) if (sa[i] >= j) y[p++] = sa[i] - j;
		for (i = 0; i < n; i++) wv[i] = x[y[i]];
		for (i = 0; i < m; i++) wts[i] = 0;
		for (i = 0; i < n; i++) wts[wv[i]]++;
		for (i = 1; i < m; i++) wts[i] += wts[i - 1];
		for (i = n - 1; i >= 0; i--) sa[--wts[wv[i]]] = y[i];
		for (t = x, x = y, y = t, p = 1, x[sa[0]] = 0, i = 1; i < n; i++)
			x[sa[i]] = cmp(y, sa[i - 1], sa[i], j) ? p - 1 : p++;
	}
}
int sa[N], rk[N], height[N];
void calheight(char *r, int *sa, int n) {
	int i, j, k = 0;
	for (i = 1; i < n; i++)rk[sa[i]] = i;
	for (i = 0; i < n - 1; height[rk[i++]] = k)
		for (k ? k-- : 0, j = sa[rk[i] - 1]; r[i + k] == r[j + k]; k++);
}

int main(){
	init_sa(s, sa, n, 256);
	calheight(s, sa, n);
}

 

回文自动机

 

struct PAM {
	int fail[N], len[N], ch[N][26], cnt[N];
	int last = 0, tot = 0, n = 0;
	int newnode(int x) {
		len[tot] = x;
		return tot++;
	}
	int get_fail(char* s, int x, int n) {
		while (s[n - len[x] - 1] != s[n])x = fail[x];
		return x;
	}
	int build(char* s) {
		s[0] = -1; fail[0] = 1; 
		newnode(0); newnode(-1);
		for (n = 1; s[n]; ++n) {
			s[n] -= 'a';
			int cur = get_fail(s, last, n);
			if (!ch[cur][s[n]]) {
				int t = newnode(len[cur] + 2);
				fail[t] = ch[get_fail(s, fail[cur], n)][s[n]];
				ch[cur][s[n]] = t;
			}
			cnt[last = ch[cur][s[n]]]++;
		}
		for (int i = tot - 1; i >= 0; i--) {
			cnt[fail[i]] += cnt[i];
		}
		return tot;//树节点个数
	}
}pam;

 

后缀自动机

 

struct SAM {
	int last, cnt;//last指针，结点数
    //child，后缀连接，最长串长度，串出现次数
	int ch[N << 1][26], fa[N << 1], len[N << 1], siz[N << 1];
	void ins(int c) {
		int p = last, np = ++cnt;
		last = np;
		len[np] = len[p] + 1;
		for (; p && !ch[p][c]; p = fa[p])ch[p][c] = np;
		if (!p)fa[np] = 1;
		else {
			int q = ch[p][c];
			if (len[p] + 1 == len[q])fa[np] = q;
			else {
				int nq = ++cnt; len[nq] = len[p] + 1;
				memcpy(ch[nq], ch[q], sizeof(ch[q]));
				fa[nq] = fa[q]; fa[q] = fa[np] = nq;
				for (; ch[p][c] == q; p = fa[p])ch[p][c] = nq;
			}
		}
		siz[np] = 1;
	}
	void build() {
		cin >> s + 1;
		int len = strlen(s + 1);
		last = cnt = 1;
		for (int i = 1; i <= len; i++) ins(s[i] - 'a');
	}
	void calc() {
		for (int i = 1; i <= cnt; i++)c[len[i]]++;
		for (int i = 1; i <= cnt; i++)c[i] += c[i - 1];
		for (int i = 1; i <= cnt; i++)a[c[len[i]]--] = i;
        //计数排序串长度从小到大
        //从长到短遍历子串，模拟DAG上dfs
		for (int i = cnt; i; i--) {
			int p = a[i];
			siz[fa[p]] += siz[p];
			if (siz[p] > 1)ans = max(ans, 1ll * siz[p] * len[p]);
		}
		cout << ans << endl;
	}
}sam;

 

struct node
{
	int ch[26];
	int len, fa;
}point[N << 1];
int las = 1, tot = 1;
void ins(int c){
	int p = las;
	int np = las = ++tot;
	point[np].len = point[p].len + 1;
	for (; p && !point[p].ch[c]; p = point[p].fa) point[p].ch[c] = np;
	if (!p) point[np].fa = 1;
	else{
		int q = point[p].ch[c];
		if (point[q].len == point[p].len + 1) point[np].fa = q;
		else{
			int nq = ++tot;
			point[nq] = point[q];
			point[nq].len = point[p].len + 1;
			point[q].fa = point[np].fa = nq;
			for (; p && point[p].ch[c] == q; p = point[p].fa) point[p].ch[c] = nq;
		}
	}
}

 

杂项

 

快读

 

namespace fastIO {
#define BUF_SIZE 100000  
	//fread -> read  
	bool IOerror = 0;
	inline char nc() {
		static char buf[BUF_SIZE], *p1 = buf + BUF_SIZE, *pend = buf + BUF_SIZE;
		if (p1 == pend) {
			p1 = buf;
			pend = buf + fread(buf, 1, BUF_SIZE, stdin);
			if (pend == p1) {
				IOerror = 1;
				return -1;
			}
		}
		return *p1++;
	}
	inline bool blank(char ch) {
		return ch == ' ' || ch == '\n' || ch == '\r' || ch == '\t';
	}
	inline void read(int &x) {
		char ch;
		while (blank(ch = nc()));
		if (IOerror)
			return;
		for (x = ch - '0'; (ch = nc()) >= '0' && ch <= '9'; x = x * 10 + ch - '0');
	}
#undef BUF_SIZE  
};
using namespace fastIO;

 

inline int read() {
    char ch = getchar(); int x = 0, f = 1;
    while(ch < '0' || ch > '9') {
        if(ch == '-') f = -1;
        ch = getchar();
    } while('0' <= ch && ch <= '9') {
        x = x * 10 + ch - '0';
        ch = getchar();
    } return x * f;
}

 

对拍

 

 数据生成data.exe

#include<bits/stdc++.h>
using namespace std;
#define random(a,b) ((a)+rand()%((b)-(a)+1))
int main() {
	int seed = time(0);
	srand(seed);
	int n = random(1, 10);
	cout << n << endl;
	for (int i = 0; i < n; i++) {
		cout << random(1, 100) << ' ' << random(1, 100) << endl;
	}
}

对拍.bat

:again
data > input.txt
biaoda < input.txt > biaoda_output.txt
test < input.txt > test_output.txt
fc biaoda_output.txt test_output.txt
if not errorlevel 1 goto again
pause

 

cb/MinGW/bin

python
import sys
sys.path.insert(0,'D:\codeblocks\MinGW\share\gcc-5.1.0\python\libstdcxx\v6')
from printers import register_libstdcxx_printers
register_libstdcxx_printers (None)
end

 

mt19937

#define random(a,b) uniform_int_distribution<int> ((a), (b))(mt)
mt19937_64 mt(chrono::steady_clock::now().time_since_epoch().count());
shuffle(a + 1, a + n + 1, mt);

 

随机树

void creatData(int n) {
	int *tree = new int[n];
	for (int i = 0; i < n; ++i) {
		tree[i] = i + 1;
	}
	int root = random(0, n - 1);
	swap(tree[root], tree[n - 1]);
	int nxt_idx = n - 2;
	queue<int> Que;
	printf("%d\n", n);
	Que.push(tree[n - 1]);
	while (!Que.empty()) {
		int now = Que.front();
		Que.pop();
		int cnt = random(1, 3);
		for (int i = 0; i < cnt; ++i) {
			int tmp_idx = random(0, nxt_idx);
			swap(tree[tmp_idx], tree[nxt_idx]);
			printf("%d %d\n", now, tree[nxt_idx]);
			Que.push(tree[nxt_idx]);
			nxt_idx--;
			if (nxt_idx == -1) break;
		}
		if (nxt_idx == -1) break;
	}
}

 

__int128

inline __int128 read()
{
    __int128 x=0,f=1;
    char ch=getchar();
    while(ch<'0'||ch>'9')
    {
        if(ch=='-')
            f=-1;
        ch=getchar();
    }
    while(ch>='0'&&ch<='9')
    {
        x=x*10+ch-'0';
        ch=getchar();
    }
    return x*f;
}

inline void write(__int128 x)
{
    if(x<0)
    {
        putchar('-');
        x=-x;
    }
    if(x>9)
        write(x/10);
    putchar(x%10+'0');
}