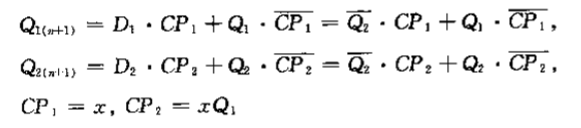组合电路

译码器

功能： $n$ 个输入变量转化为 $2^n$ 个输出变量。2进制转10进制。输出外部取反。

例：3-8译码器

把函数转化为析取式，（析取式与合取式互补），再取极小项对应的下标即可。

连接时使能端要全连通，极小项的从高位向低位，连接译码器的高向低。

注意若输出端取反了，则实际输出是极小项的反，不能直接用。

数据选择器

功能：从 $2^n$ 个输入选择一个输出。最多接受 $n+1$ 个变量。

例：4选1数据选择器

同样把函数化为积之和。
选定一个变量作为数据端，若规定了不能取反，则只能选择在函数中只以原变量的形式出现的变量。
把函数以其它 $n$ 个变量二进制递增的形式排好序。
按照二进制由低位向高位分别由上到下连接数据选择端，（与译码器相反）。另一个变量与1，0，按照二进制位对应连接数据端。

数据选择器与译码器的数据端连接顺序不同，译码器直接从左到右连接从上到下，数据选择器按照二进制位对应连接。

优先编码器

功能：10进制转2进制。输入和输出外部都取反。

例：8-3编码器

仅当控制端选通，且输入存在1，即选通且正在编码， $Y_s$ 为1，实际取反为0.

仅当控制端选通，且输入全为0，即选通但未编码， $E_x$ 为1，实际取反为0.

扩展：第 1 级的 $E_x$ 连接第 2 级的控制端，且第 1 级的优先级大于第 2 级。仅当第 1 级无输入， $E_x$ 取反才是0，才会轮到第 2 级。

全加器

$S=A \bigoplus B \bigoplus C_i\\ =\overline{C_i} \overline{A}B+\overline{C_i}A\overline{B}+C_i\overline{A}\overline{B}+C_iAB$

进位 $C_i$

$C_i=AB+AC_i+C_iB$

触发器

RS触发器

$Q_{n+1}=S+\overline{R}Q_n$

激励表

功能：置位端S，复位端R。

$S$ 为 1， $Q_{n+1}$ 为 1； $R$ 为 1， $Q_{n+1}$ 为 0； $S,R$ 都为 0，保持 $Q_n$ 不变。

$S,R$ 不能都为 1.

JK触发器

$Q_{n+1}=J\overline{Q_n}+\overline{K}Q_n$

激励表

功能：与RS触发器类似，新增 JK=11 时翻转 $Q_n$ 。

D触发器

$Q_{n+1}=D$

激励表

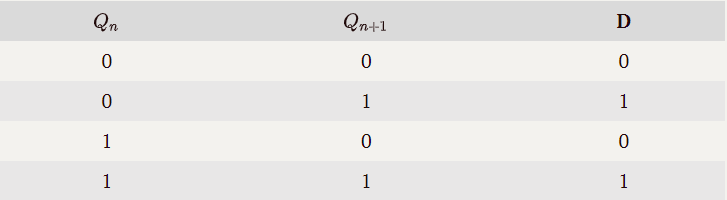
功能：次态始终等于激励

T触发器

$Q_{n+1}=T\overline{Q_n}+\overline{T}Q_n$

激励表

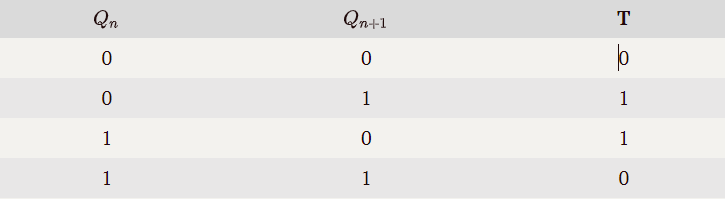
功能：T 为 1 时，翻转 $Q_n$

四种触发器的转换

例1：JK触发器构成D和T触发器

将对象触发器的状态方程写为已有触发器的状态方程类似形式。

D触发器方程：

$Q_{n+1}=D\\ \implies Q_{n+1}=D\overline{Q_{n}}+DQ_{n}$

与已知触发器JK触发器方程对比：

$Q_{n+1}=J\overline{Q_n}+\overline{K}Q_n$

对应取值

$J=D,\overline{K}=D\\ \implies J=D,K=\overline{D}$

T触发器方程：

$Q_{n+1}=T\overline{Q_n}+\overline{T}Q_n\\ \implies J=T,K=T$

例2：D触发器构成JK和T触发器

直接取 $D=$ 对象触发器的 $Q_{n+1}$

JK触发器：

$D=J\overline{Q_n}+\overline{K}Q_n$

T触发器：

$D=T\overline{Q_n}+\overline{T}Q_n$

边沿触发器

触发器CP接口处有三角符号代表是边沿触发。

若接口处还有⭕，代表是负边沿触发，反之正边沿触发。

计数器

二进制计数器

属于异步计数器

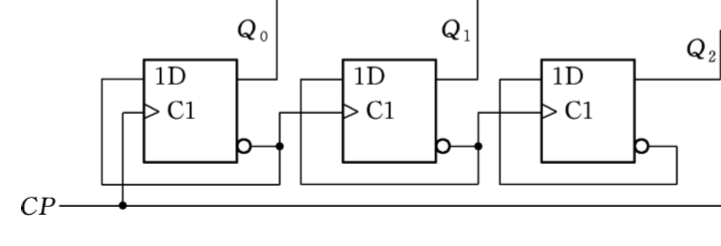
总之，若上升沿触发，且后级时钟来自前级输出，则为减法计数器（倒计时）。

同步时序电路

两种模型

米利模型：输出与输入直接相关

米利模型比摩尔模型提前一个时钟周期改变输出。

摩尔模型的状态通常多于米利模型，因为它把统一现态，不同输出也作为不同状态。

若要求输出保持一个时钟周期，则必须使用摩尔模型。

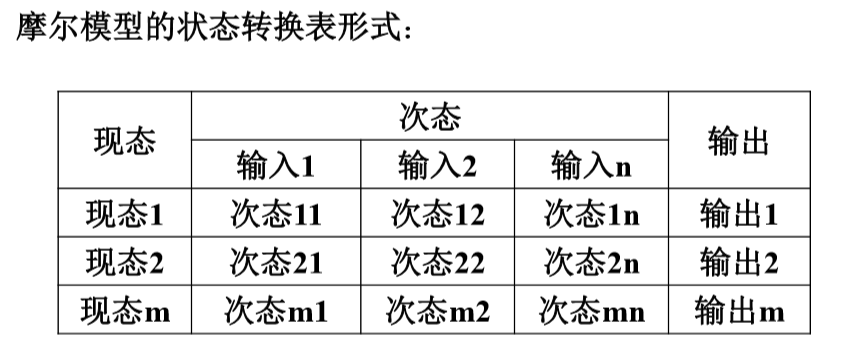
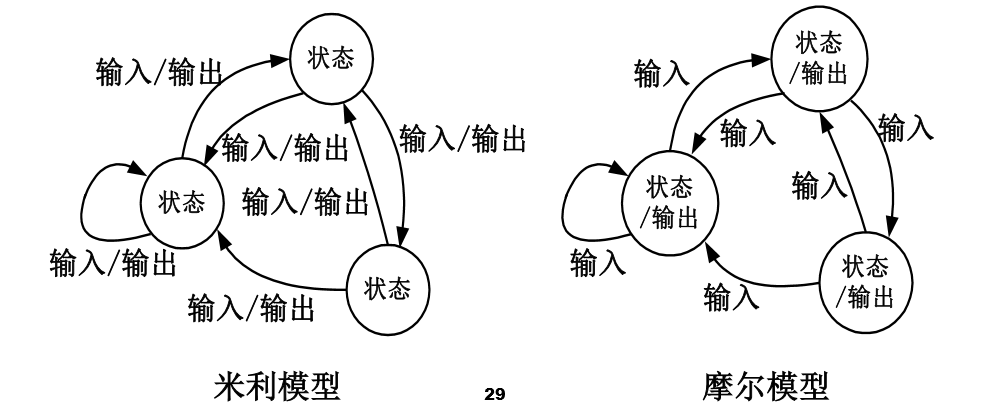
分析

确定模型类型（米利/摩尔），若输出直接与输入相关，则必须米利；若要求保持一个周期，则必须摩尔。
写出激励方程：

$J_1=XQ_2,K_1=Q_1;\\J_2=\overline{X},K_2=XQ_1$
代入得到状态方程：

$Q_{1(n+1)}=J_1\overline{Q_1}+\overline{K_1}Q_1=X\overline{Q_1}Q_2\\ Q_{2(n+1)}=J_2\overline{Q_2}+\overline{K_2}Q_2=\overline{X}\overline{Q_2}+\overline{XQ_1}Q_2$

写出输出方程：

$Z=Q_1Q_2$
列出对应模型的状态转换表并编码
画出对应模型的状态转换图
画出时序图，分析功能

设计

确定模型
画出状态转换图
列出状态转换表并编码
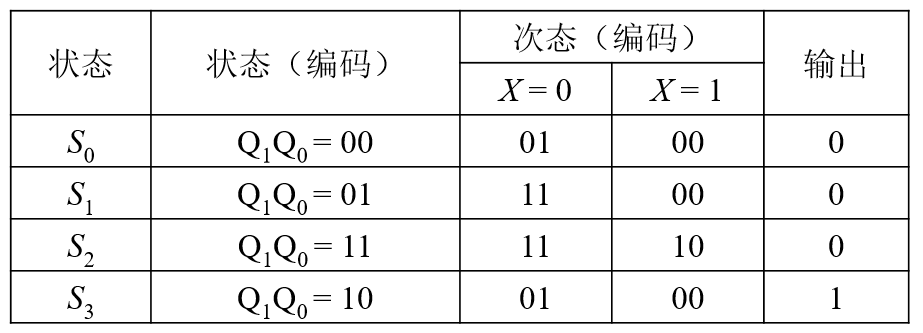
合并相同状态
选定触发器
根据触发器的激励表，写出状态激励表
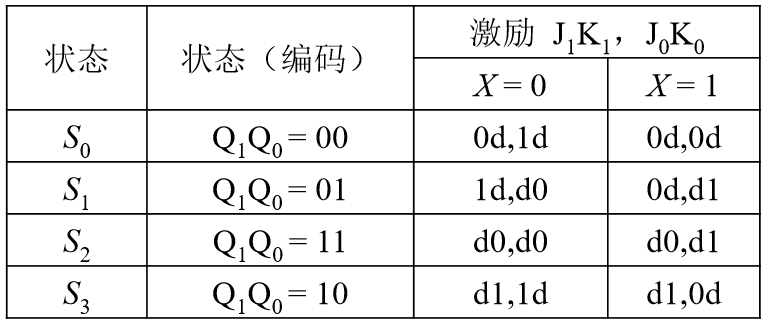
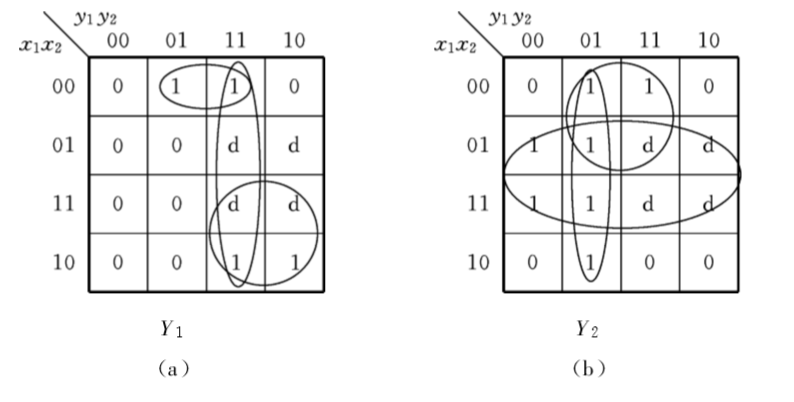
对于每一个激励 $J_1,K_1,J_2,K_2$ 画出卡诺图，确定激励函数。
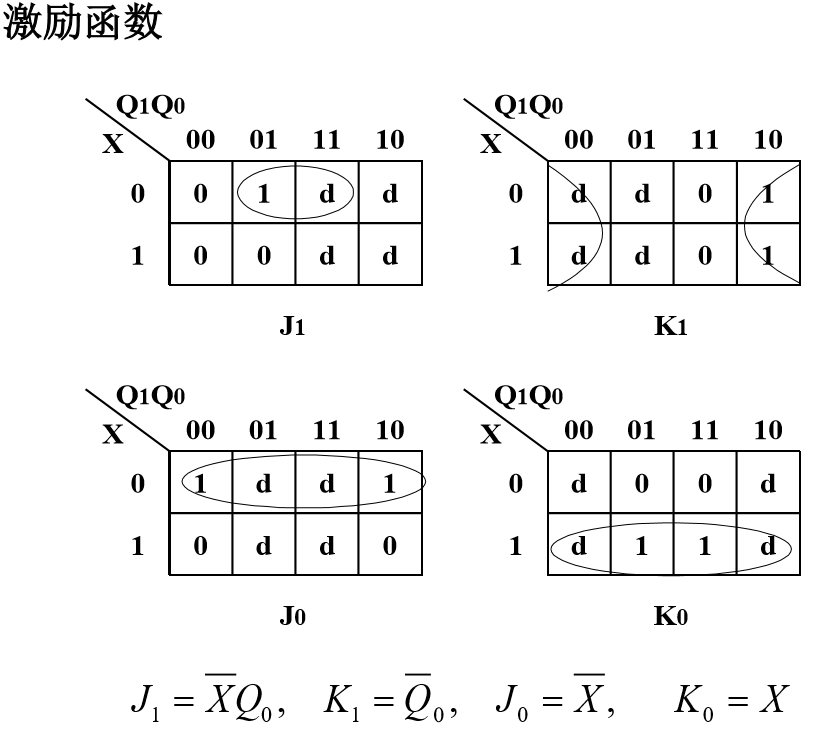
对于输出 $Z$ ，与以上相同，画出卡诺图，确定输出函数。
画出电路图

异步时序电路

基本型异步时序电路

概念

没有触发器，输入信号为电平信号

激励状态 $Y_1,Y_2$ 与系统状态 $y_1,y_2$ 之间存在延时。

分析

写出激励函数和输出函数

$Y_1=\overline{x_1}x_2\overline{y_2}+x_2y_1\overline{y_2}+x_1y_1\\ Y_2=x_1y_1+x_2y_2\\ Z=\overline{x_1y_1}$
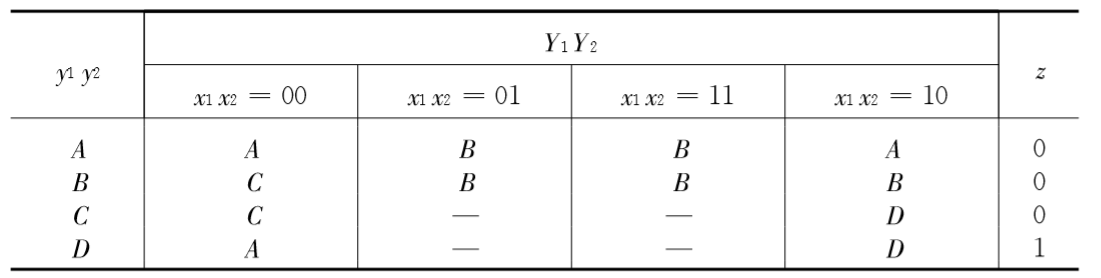
写出状态流程表，并确定稳定状态（ $y_1,y_2=Y_1,Y_2$ ）
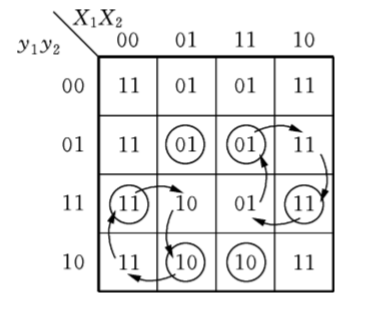
根据给定的输入序列，得到序列下的系统总态。只要求最终的稳态，不要中间过程。
画出时序图，注意 $y_1,y_2$ 与 $Y_1,Y_2$ 之间存在延时，输出也存在较短延时。

设计

分析定义状态
画出转换图，列出转换表
状态编码，表中相邻状态只有一位改变
画出激励态卡诺图，写出激励函数和输出函数，注意不能产生冒险
画出电路图

脉冲型异步时序电路

概念

有触发器，且触发器的CP并不统一。边沿触发。

触发器的状态方程中应包含CP。

没有延迟

例：JK触发器

$Q_{n+1}=(J\overline{Q_n}+\overline{K}Q_n)\cdot CP+Q_n\cdot \overline{CP}$

D触发器

$Q_{n+1}=D\cdot CP+Q_n\cdot \overline{CP}$

分析

根据电路图写出状态方程，包括CP
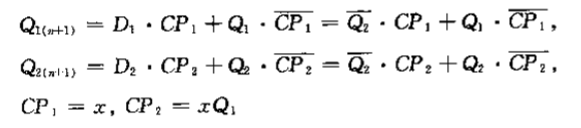
列出所有可能状态，建立表格。

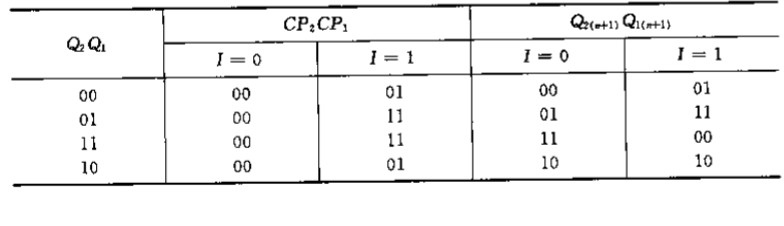
I=1 表示有效边沿跳变。
画出状态转化图，直接用边沿跳变代替输入。
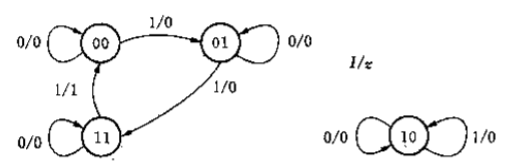
画出时序图。

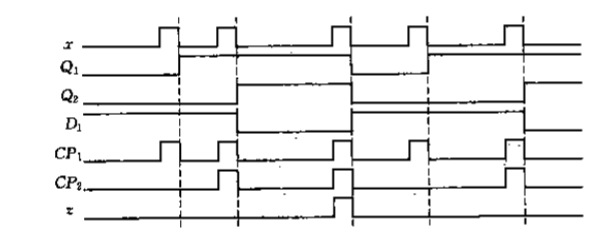
设计

定义状态
画出状态转化图，列出状态转化表，编码
若需要CP信号且CP不同，则需要确定CP信号。

可以通过观察时序图，若某一信号在当前信号每次变化时都有有效边沿跳变，则可以选取它作为CP。
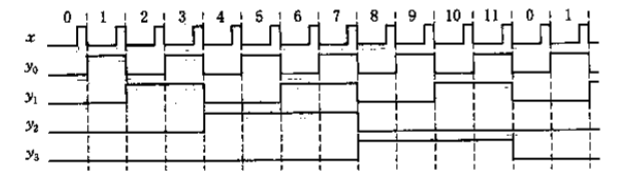
根据状态转化表和触发器的激励表，确定激励函数，输出函数。

注意只需要选取CP的有效触发处的现态和次态

如上图 $y_2,y_3$ 将 $y_1$ 作为CP，而 $y_1$ 只在3，7，11处有负边沿触发。

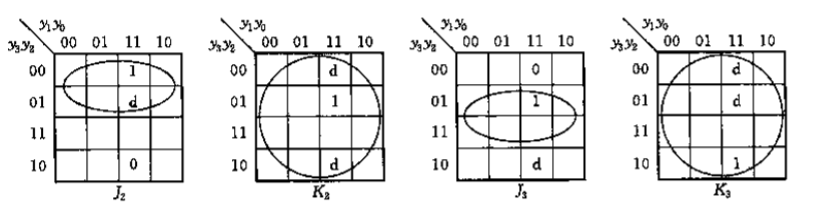
若有多个输入，则不能跨输入画卡诺圈
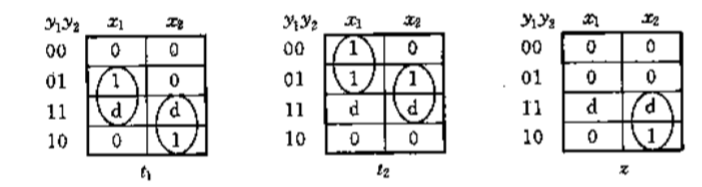
画出电路图。