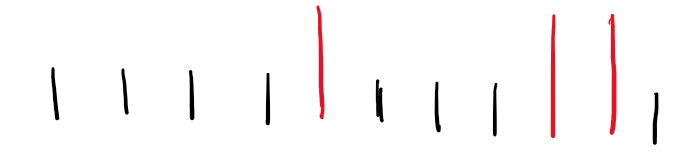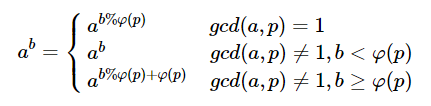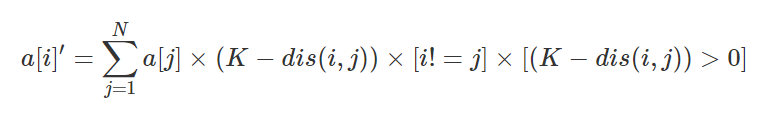数论专题

牛牛与LCM

题意：问能否从 n 个数中选出一些数，使得lcm=x。

把所有 x 的因子都选出来，看lcm如果不等于x，则不行，否则行。

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int INF = 0x3f3f3f3f;
const ll inf = 0x3f3f3f3f3f3f3f3f;
const int N = 2e6 + 10;
const ll mod = 998244353;
int n; ll x;
ll a[N], lcm = -1;
int gcd(int a, int b) {
	if (a < b)swap(a, b);
	return b == 0 ? a : gcd(b, a%b);
}
int main() {
	scanf("%d", &n);
	for (int i = 1; i <= n; i++) scanf("%lld", &a[i]);
	scanf("%lld", &x);
	for (int i = 1; i <= n; i++) {
		if (x%a[i] == 0) {
			if (lcm == -1) {
				lcm = a[i];
			}
			else {
				lcm = lcm * a[i] / gcd(lcm, a[i]);
			}
		}
	}
	puts(lcm == x ? "Possible" : "Impossible");
	return 0;
}

 

集合中的质数

 

题意：给出一个集合和一个数m。 集合里面有n个质数。 请你求出从 1 到 m 的所有数中，至少能被集合中的一个数整除的数的个数。

容斥

注意lcm过大时跳出dfs。

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int INF = 0x3f3f3f3f;
const ll inf = 0x3f3f3f3f3f3f3f3f;
const int N = 2e6 + 10;
const ll mod = 998244353;
int n;
ll m;
ll a[N], ans;
ll gcd(ll a, ll b) {
	if (a < b)swap(a, b);
	return b == 0 ? a : gcd(b, a%b);
}
ll lcm(ll a, ll b) {
	return a * b / gcd(a, b);
}
ll c[N];
void dfs(ll x, int id, int cnt) {
	if (x > m)return;
	if (id >= n + 1) {
		if (cnt > 0) {
			c[cnt] += m / x;
		}
		return;
	}
	if (x == -1)dfs(a[id], id + 1, cnt + 1);
	else dfs(lcm(x, a[id]), id + 1, cnt + 1);
	dfs(x, id + 1, cnt);
}
int main() {
	scanf("%d%lld", &n, &m);
	for (int i = 1; i <= n; i++)scanf("%lld", &a[i]);
	dfs(-1, 1, 0);
	for (int t = 1; t <= n; t++) {
		if (t & 1)ans += c[t];
		else ans -= c[t];
	}
	printf("%lld\n", ans);
	return 0;
}

 

珂朵莉的数论题

 

题意：求：第x小的正整数v使得其最小的质因数为质数y，即正好有x-1个[1,v-1]之内的正整数满足其最小的质因数为质数y。 若答案超过1000000000则输出0。

二分+容斥+枚举

找恰好第 x 个数，第一反应应该是二分，而只有当 y 足够小时，可以通过容斥从所有 y 的倍数中去掉 y 小的质数的倍数。

60为第18个质数（应该是），这时可以容斥。

如果y大于60，则只能枚举，并且复杂度也允许枚举。只枚举y的倍数，并暴力枚举小于y的数，从中去掉它们的倍数，最终剩下的都是符合条件的数，只要计数即可。

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int INF = 0x3f3f3f3f;
const ll inf = 0x3f3f3f3f3f3f3f3f;
const int N = 2e7 + 10;
const ll mod = 998244353;
ll x, y;
int prime[100];
int vis[100], cnt;
int sieve(int n) {
	cnt = 0;
	for (int i = 2; i <= n; i++) {
		if (!vis[i]) {
			vis[i] = i;
			prime[cnt++] = i;
		}
		for (int j = 0; j < cnt; j++) {
			if (i*prime[j] > n)break;
			vis[i*prime[j]] = prime[j];
			if (i%prime[j] == 0)break;
		}
	}
	return cnt;
}
bool die[N];
ll gcd(ll a, ll b) {
	if (a < b)swap(a, b);
	return b == 0 ? a : gcd(b, a%b);
}
ll lcm(ll a, ll b) {
	return a * b / gcd(a, b);
}
ll tmp[100];
void dfs(ll up, ll x, int dep, int cnt) {
	if (x > up)return;
	if (prime[dep] >= y) {
		if (cnt > 0)tmp[cnt] += up / x;
		return;
	}
	dfs(up, lcm(x, prime[dep]), dep + 1, cnt + 1);
	dfs(up, x, dep + 1, cnt);
}
int m;
ll cal(ll n) {
	memset(tmp, 0, sizeof(tmp));
	dfs(n, y, 0, 0);
	ll ans = n / y;
	for (int i = 1; i <= m; i++) {
		if (i & 1)ans -= tmp[i];
		else ans += tmp[i];
	}
	return ans;
}
int main() {
	sieve(80);
	scanf("%lld%lld", &x, &y);
	for (int i = 0; prime[i] < y; i++)m++;
	if (y >= 60) {
		ll ans = 0, c = 0;
		for (int i = 2; i < y; i++) {
			if (!die[i])for (int j = i; j <= 1000000000 / y; j += i) {
				die[j] = 1;
			}
		}
		for (int i = 1; i <= 1000000000 / y; i++) {
			if (!die[i]) {
				c++;
				if (c == x) {
					ans = i * y;
					break;
				}
			}
		}
		printf("%lld\n", ans);
	}
	else {
		ll L = 1, R = 1000000010;
		while (L < R) {
			ll mid = (L + R) / 2;
			if (cal(mid) < x)L = mid + 1;
			else R = mid;
		}
		printf("%lld\n", L > 1000000000 ? 0 : L);
	}
	return 0;
}

 

欧拉

 

题意：求 $F(n)=\sum_{d|n}d^k\mu(\frac{n}{d})$

欧拉筛

$F=ID_k*\mu$，这两个都是积性函数，迪利克雷卷积后还是积性，所以可以对 F 用欧拉筛。

$F(p^n)=\sum_{d|p^n}d^{nk}\mu(\frac{p^n}{d})$，d 为 1 或 p 时不为 0.

所以 $F(p^n)=d^{nk}(1-\frac{1}{d^k})$。

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int INF = 0x3f3f3f3f;
const ll inf = 0x3f3f3f3f3f3f3f3f;
const int N = 5e6 + 10;
const ll mod = 998244353;
int m, k, n;
ll f[N], prime[N], cnt;
bool vis[N];
ll Pow(ll a, ll b) {
	ll res = 1ll;
	while (b) {
		if (b & 1)res = res * a%mod;
		a = a * a%mod;
		b >>= 1;
	}
	return res;
}
ll idk[N], invk[N], d;
void sieve(int n) {
	f[1] = 1;
	for (int i = 2; i <= n; i++) {
		if (!vis[i]) {
			prime[cnt++] = i;
			idk[i] = Pow(i, k);
			invk[i] = Pow(idk[i], mod - 2);
			f[i] = idk[i] * (1 + mod - invk[i]) % mod;
		}
		for (int j = 0; j < cnt && (d = i * prime[j]) <= n; j++) {
			vis[d] = 1;
			if (i%prime[j] == 0) {
				f[d] = f[i] * idk[prime[j]] % mod;
				break;
			}
			else {
				f[d] = f[i] * f[prime[j]] % mod;
			}
		}
	}
}
int main() {
	scanf("%d%d", &m, &k);
	sieve(5000000);
	while (m--) {
		scanf("%d", &n);
		printf("%lld\n", f[n]);
	}
	return 0;
}

 

一个小问题

 

题意：给你k对a和r是否存在一个正整数x使每队a和r都满足：x mod a=r，求最小正解x或无解。

扩展中国剩余定理

模板题

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int INF = 0x3f3f3f3f;
const ll inf = 0x3f3f3f3f3f3f3f3f;
const int N = 5e6 + 10;
const ll mod = 998244353;
ll x, y;
ll gcd(ll a, ll b) {
	if (a < b)swap(a, b);
	return b == 0 ? a : gcd(b, a % b);
}
ll exgcd(ll a, ll b, ll &x, ll &y) {
	if (b == 0) { x = 1, y = 0; return a; }
	ll r = exgcd(b, a % b, x, y), tmp;
	tmp = x; x = y; y = tmp - (a / b) * y;
	return r;
}
ll inv(ll a, ll b) {
	ll r = exgcd(a, b, x, y);
	while (x < 0) x += b;
	return x;
}
ll excrt(ll* M, ll* C, int n) {
	for (int i = 2; i <= n; i++) {
		ll M1 = M[i - 1], M2 = M[i], C2 = C[i], C1 = C[i - 1], T = gcd(M1, M2);
		if ((C2 - C1) % T != 0) return -1;
		M[i] = (M1 * M2) / T;
		C[i] = (inv(M1 / T, M2 / T) * (C2 - C1) / T) % (M2 / T) * M1 + C1;
		C[i] = (C[i] % M[i] + M[i]) % M[i];
	}
	return C[n];
}
int n;
ll M[N], C[N];
int main() {
	scanf("%d", &n);
	for (int i = 1; i <= n; i++)scanf("%lld%lld", &M[i], &C[i]);
	printf("%lld\n", excrt(M, C, n));
	return 0;
}

 

n的约数

 

题意：t次询问，每次给你一个数n，求在[1,n]内约数个数最多的数的约数个数。t <= 500 , 1 <= n <= 1e18

dfs

显然在质因子的幂次相同的情况下，质因子越小越好。所以考虑把数量最大的质因子都向前靠。

设 $x=\prod p_i^{k_i}$，满足 $k[i]$ 单调不递增。即 $k_i\le k_{i-1}$。

由于 $\sum k_i\le \log n$，所以复杂度必能过。

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int INF = 0x3f3f3f3f;
const ll inf = 0x3f3f3f3f3f3f3f3f;
const int N = 5e6 + 10;
const ll mod = 998244353;
ll n;
int T;
int a[N];
int prime[N];
bool is_prime[N];
int vis[N], cnt;
int euler_sieve(int n) {
	memset(vis, 0, sizeof(vis));
	memset(prime, 0, sizeof(prime));
	for (int i = 2; i <= n; i++) {
		if (!vis[i]) { vis[i] = i; prime[cnt++] = i; is_prime[i] = true; }
		for (int j = 0; j < cnt; j++) {
			if (i*prime[j] > n)  break;
			vis[i*prime[j]] = prime[j];
			if (i%prime[j] == 0)
				break;
		}
	}
	return cnt;
}
ll ans;
ll p[100][100];
void dfs(ll x, int dep) {
	if (x < prime[dep]) {
		ll tmp = 1;
		for (int i = 0; i < dep; i++)tmp *= (a[i] + 1);
		ans = max(ans, tmp);
		return;
	}
	for (a[dep] = 1; (dep == 0 || a[dep] <= a[dep - 1]) && p[dep][a[dep]] <= x; a[dep]++)
		dfs(x / p[dep][a[dep]], dep + 1);
}
int main() {
	cnt = euler_sieve(100);
	for (int i = 0; i < 100; i++) {
		p[i][0] = 1;
		for (int j = 1; j < 100; j++)p[i][j] = p[i][j - 1] * prime[i];
	}
	scanf("%d", &T);
	while (T--) {
		for (int i = 0; i < 100; i++)a[i] = 0;
		scanf("%lld", &n);
		ans = 0;
		dfs(n, 0);
		printf("%lld\n", ans);
	}
	return 0;
}

 

黑猫的小老弟

 

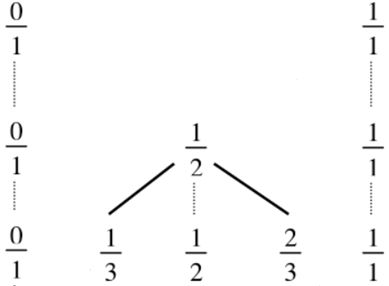
题意：初始有0/1和1/1，每层先从小到大排列，相邻两项分子分母分别相加，得到新的分数，与已有的一起作为下一代，每个分数都约分简化，若分子或分母大于n，则去掉，问第 n 层有多少数。

法利数列

法利数列生成的过程中就始终是有序的。

第n层为前n个欧拉函数值之和。

如第4层，以4为分母的分数分子有1，3；以3为分母的分数分子有1，2；以2为分母的分子有1。即每层都是达到“最完整”。

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int INF = 0x3f3f3f3f;
const ll inf = 0x3f3f3f3f3f3f3f3f;
const int N = 5e6 + 10;
const ll mod = 998244353;
int T;
int n;
bool vis[N];
ll prime[N], phi[N], cnt;
void sieve(int n) {
	for (int i = 2; i <= n; i++) {
		if (!vis[i]) {
			prime[cnt++] = i;
			phi[i] = i - 1;
		}
		ll d;
		for (int j = 0; j < cnt && (d = i * prime[j]) <= n; j++) {
			vis[d] = 1;
			if (i%prime[j] == 0) {
				phi[d] = phi[i] * prime[j];
				break;
			}
			else {
				phi[d] = phi[i] * phi[prime[j]];
			}
		}
	}
}
ll sum[N];
int main() {
	sieve(10000);
	for (int i = 1; i <= 10000; i++)sum[i] = sum[i - 1] + phi[i];
	scanf("%d", &T);
	while (T--) {
		scanf("%d", &n);
		printf("%lld\n", sum[n] + 2);
	}
	return 0;
}

 

托米的游戏

 

题意：托米有一棵有根树 T, 树根为1，每轮他会在剩下的子树中等概率一个点 u, 砍掉 u 的子树 (包含 u)，如果树上的点都被砍光了，游戏结束。问游戏的期望轮数。模998244353.

由于期望可加性，所有点都被去掉的期望等于各个点单独被去掉的期望的和。

所以我们需要求每个点被去掉的情况下期望的对该点操作的次数。

这是一个条件概率，并且要注意是对该点操作，而不包含对其它点的操作。这样求和之后才是最终期望。

共有 dep[u] 个选择可以去掉该点（该点及其祖先）。只有对该点的操作产生1的贡献，所以期望就是 1/dep[u]。

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int INF = 0x3f3f3f3f;
const ll inf = 0x3f3f3f3f3f3f3f3f;
const int N = 5e6 + 10;
const ll mod = 998244353;
int n;
vector<int>G[N];
int dep[N];
void dfs(int u, int _fa) {
	for (int v : G[u]) {
		if (v == _fa)continue;
		dep[v] = dep[u] + 1;
		dfs(v, u);
	}
}
ll Pow(ll a, ll b) {
	ll res = 1ll;
	while (b) {
		if (b & 1)res = res * a%mod;
		a = a * a%mod;
		b >>= 1;
	}
	return res;
}
int main() {
	scanf("%d", &n);
	for (int i = 1; i < n; i++) {
		int u, v;
		scanf("%d%d", &u, &v);
		G[u].push_back(v);
		G[v].push_back(u);
	}
	dep[1] = 1;
	dfs(1, 0);
	ll ans = 0;
	for (int i = 1; i <= n; i++) {
		ans = (ans + Pow(dep[i], mod - 2)) % mod;
	}
	printf("%lld\n", ans);
	return 0;
}

 

[HAOI2007]反素数ANT

 

题意：求一个不超过n的最大的数x，满足它的因数个数严格大于每个小于它的数的因数个数。

dfs

和上面那道“n的因数”类似。

本题实际上是要求最小的含有最多因数的数。

如上图，红色都是有最多因数的数。首先肯定是要求红色，其次，还必须是第一个红色。因为后面的红色不能满足前面所有数的因数个数严格小于它。

所以只要在枚举时记录一下因数个数最多的数的大小，取最小值即可。

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define debug(x) cout << #x << ":\t" << x << endl;
const int INF = 0x3f3f3f3f;
const ll inf = 0x3f3f3f3f3f3f3f3f;
const int N = 2e5 + 10;
const ll mod = 998244353;
int prime[N];
int cnt;
ll n;
int vis[N];
void sieve(int n) {
	cnt = 0;
	int d = 0;
	for (int i = 2; i <= n; i++) {
		if (!vis[i]) {
			prime[cnt++] = i;
		}
		for (int j = 0; j < cnt && (d = i * prime[j]) <= n; j++) {
			vis[d] = 1;
			if (i%prime[j] == 0) {
				break;
			}
		}
	}
}
int a[110];
ll ans, id;
void dfs(ll x, int dep) {
	if (x * prime[dep] > n) {
		ll tmp = 1;
		//debug(x)
		for (int i = 0; i < dep; i++) {
			tmp *= (a[i] + 1);
		}
		if (tmp > ans) {
			ans = tmp;
			id = x;
		}
		else if (ans == tmp) {
			id = min(id, x);
		}
		return;
	}
	ll p = prime[dep];
	for (a[dep] = 1; (dep == 0 || a[dep] <= a[dep - 1]) && x*p <= n; a[dep]++, p *= prime[dep]) {
		dfs(x*p, dep + 1);
	}
}

int main() {
	scanf("%lld", &n);
	sieve(200000);
	dfs(1, 0);
	printf("%lld\n", id);
	return 0;
}

 

禁止动规

 

题意：有n个正整数，每个数范围1到m，如果能用这些数任意加减得到1（每个数可以重复使用或不用），则这个数列可行，问有几种可行数列。模 $2^{64}$。

杜教筛+分块

先观察出条件等价于 $gcd(x_1,x_2,\cdots,x_n)=1$。

则要求

$$\begin{align} ans &= \sum_{x_1=1}^m\sum_{x_2=1}^m\cdots\sum_{x_n=1}^m[gcd(x_1,x_2,\cdots,x_n)=1]\\ &= \sum_{x_1=1}^m\sum_{x_2=1}^m\cdots\sum_{x_n=1}^m\sum_{d|gcd(x_1,\cdots,x_n)}\mu(d)\\ &= \sum_{d=1}^m(\lfloor\frac{m}{d}\rfloor)^n\mu(d)\\ \end{align}$$

对于 $\lfloor\frac{m}{d}\rfloor$ 分块求，每块的 $\lfloor\frac{m}{d}\rfloor$ 相同，所以只要知道 $\sum_{d=l}^r\mu(d)$ 即可。

用杜教筛求 $\sum_{d=l}^r\mu(d)$。

题目还要求对 $2^{64}$ 取模，可以直接把所有变量都定义为 unsigned long long，这样自然溢出就相当于取模了。

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define debug(x) cout << #x << ":\t" << x << endl;
#define ull unsigned ll
const int INF = 0x3f3f3f3f;
const ll inf = 0x3f3f3f3f3f3f3f3f;
const int N = 1e7 + 10;
ull n, m;
int vis[N], prime[N], mu[N], cnt;
map<ull, ull>mp;
void pre(int n) {
	mu[1] = 1;
	ll d;
	for (int i = 2; i <= n; i++) {
		if (!vis[i]) {
			prime[cnt++] = i;
			mu[i] = -1;
		}
		for (int j = 0; j < cnt && (d = i * prime[j]) <= n; j++) {
			vis[d] = 1;
			if (i%prime[j] == 0) {
				mu[d] = 0;
				break;
			}
			else {
				mu[d] = -mu[i];
			}
		}
	}
	for (int i = 1; i <= n; i++)mu[i] += mu[i - 1];
}
ull Pow(ull a, ull b) {
	ull res = 1ull;
	while (b) {
		if (b & 1)res = res * a;
		a = a * a;
		b >>= 1;
	}
	return res;
}
ull ans;
ull cal(ull n) {
	if (n < N)return mu[n];
	if (mp.count(n))return mp[n];
	ull res = 0;
	for (ull l = 2, r; l <= n; l = r + 1) {
		r = n / (n / l);
		res = res + (r - l + 1)*cal(n / l);
	}
	return mp[n] = (1 - res);
}
int main() {
	scanf("%llu%llu", &n, &m);
	pre(N - 1);
	for (ull l = 1, r; l <= m; l = r + 1) {
		r = m / (m / l);
		ull tmp = Pow(m / l, n);
		ans = ans + (cal(r) - cal(l - 1))*tmp;
	}
	printf("%llu\n", ans);
	return 0;
}

 

[HAOI2011]向量

 

题意：给你一对数a,b，你可以任意使用(a,b), (a,-b), (-a,b), (-a,-b), (b,a), (b,-a), (-b,a), (-b,-a)这些向量，问你能不能拼出另一个向量(x,y)。 说明：这里的拼就是使得你选出的向量之和为(x,y)

斐蜀定理

设 $(x,y)=A(a,b)+B(a,-b)+C(b,a)+D(b,-a)$，其他的向量都可以取负变成这四个中某个。

$$\begin{cases} (A+B)a+(C+D)b=x\\ (C-D)a+(A-B)b=y\\ \end{cases}$$

$a,b$ 已知，所以把 A，B，C，D 视为未知数，求解方程组，每个方程单独考虑，有整数解等价于

$$\begin{cases} gcd(a,b)|x\\ gcd(a,b)|y\\ \end{cases}$$

但是这并只能保证 $A+B,A-B$ 分别为整数，而 $A,B$ 不能保证，还要求出 $A=\frac{(A+B)+(A-B)}{2}$ 有整数解，也就是 $A+B,A-B$ 奇偶性相同。

分类讨论：

1. $A+B,A-B$ 为偶，$C+D,C-D$ 为偶。则提出一个 2，方程组变为

   $$\begin{cases} \frac{A+B}{2}\cdot 2a+\frac{C+D}{2}\cdot 2b=x\\ \frac{C-D}{2}\cdot 2a+\frac{A-B}{2}\cdot 2b=y\\ \end{cases}$$

   判断

   $$\begin{cases} gcd(2a,2b)|x\\ gcd(2a,2b)|y\\ \end{cases}$$

2. $A+B,A-B$ 为奇，$C+D,C-D$ 为偶。则两边先加 a，凑成偶数。再用上面的方法。

   $$\begin{cases} \frac{A+B+1}{2}\cdot 2a+\frac{C+D}{2}\cdot 2b=x+a\\ \frac{C-D}{2}\cdot 2a+\frac{A-B+1}{2}\cdot 2b=y+b\\ \end{cases}$$

   判断

   $$\begin{cases} gcd(2a,2b)|(x+a)\\ gcd(2a,2b)|(y+b)\\ \end{cases}$$

3. $A+B,A-B$ 为偶，$C+D,C-D$ 为奇。同理。

   判断

   $$\begin{cases} gcd(2a,2b)|(x+b)\\ gcd(2a,2b)|(y+a)\\ \end{cases}$$

4. $A+B,A-B$ 为奇，$C+D,C-D$ 为奇。同理。

   判断

   $$\begin{cases} gcd(2a,2b)|(x+b+a)\\ gcd(2a,2b)|(y+a+b)\\ \end{cases}$$

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define debug(x) cout << #x << ":\t" << x << endl;
#define ull unsigned ll
const int INF = 0x3f3f3f3f;
const ll inf = 0x3f3f3f3f3f3f3f3f;
const int N = 2e5 + 10;
int T;
ll a, b, x, y;
ll gcd(ll a, ll b) {
	if (a < b)swap(a, b);
	return b == 0 ? a : gcd(b, a%b);
}
bool ck(ll g, ll x, ll y) {
	return x % g == 0 && y % g == 0;
}
int main() {
	scanf("%d", &T);
	while (T--) {
		scanf("%lld%lld%lld%lld", &a, &b, &x, &y);
		if (a == 0 && b == 0) {
			puts(x == 0 && y == 0 ? "Y" : "N");
			continue;
		}
		ll g = gcd(abs(a), abs(b));
		if (x%g || y % g) { puts("N"); continue; }
		g = gcd(abs(2 * a), abs(2 * b));
		if (ck(g, x, y) || ck(g, x + a + b, y + a + b) || ck(g, x + a, y + b) || ck(g, x + b, y + a))puts("Y");
		else puts("N");
	}
	return 0;
}

 

[AHOI2007]密码箱

 

题意：给定 n，找出所有 $x^2=1(\mod n)$ 的 x。

枚举

$$(x-1)(x+1)=kn\\ (x-1)(x+1)=k_1n_1\cdot k_2n_2\\$$

枚举 $n_1$，对于每个 $n_1$，算出 $n_2$，再枚举 $k_2$，$k_2n_2=(x-1)$ 或 $k_2n_2=(x+1)$，算出 $x$ ，再判断 $k_1$ 是否为整数。

本题枚举复杂度够的关键点就在于只枚举 $n_1\leq \sqrt{n}$，这样 $n_2\ge \sqrt{n}$， $n/n_2\le \sqrt{n}$，$k_2$ 从 1 到 $n_1$，所以复杂度是 n 的所有小于 $\sqrt{n}$ 的因子之和，$O(\sqrt{n}\log n)$。

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define debug(x) cout << #x << ":\t" << x << endl;
#define ull unsigned ll
const int INF = 0x3f3f3f3f;
const ll inf = 0x3f3f3f3f3f3f3f3f;
const int N = 2e5 + 10;
const ll mod = 998244353;
ll n;
set<int>st;
int main() {
	scanf("%lld", &n);
	if (n == 1) { puts("None"); return 0; }
	for (int n1 = 1; n1*n1 <= n; n1++) {
		if (n%n1)continue;
		int n2 = n / n1;
		for (int k2 = 1; k2*n2 - 1 < n; k2++) {
			int x = n2 * k2 - 1;
			if ((x - 1) % n1 == 0)st.insert(x);
		}
		for (int k2 = 1; k2*n2 + 1 < n; k2++) {
			int x = n2 * k2 + 1;
			if ((x + 1) % n1 == 0)st.insert(x);
		}
	}
	st.insert(1);
	for (int u : st)printf("%d\n", u);
	return 0;
}

 

[SCOI2009]游戏

 

题意：有一个对应关系，1到n每个数与除自己外某个1到n的数一一对应，初始序列为 $1,2,\cdots,n$ ，根据对应关系进行置换，设变回 $1,2,\cdots,n$ 需要 t 行，问对所有对应关系，共有几种不同的 t。

dp

所有变换构成几个环，变回去需要的行数等于这些环长度的 LCM。而这些环长度和等于 n。

所以问题变为把 n 分解成一个数列，问数列的LCM有多少种。

$lcm(x,y)=x*y/gcd(x,y)$，gcd 不好处理，但是如果 x，y 互质，就不用考虑 gcd 了。

如果一些数的和小于 n，可以补 1，不会影响 LCM。

所以只要求出所有满足和小于等于 n 的质数集合，集合中所有数的乘积就是LCM，由唯一分解定理容易知道每个集合对应不同的LCM。

$dp[i][j]$ 表示前 i 个质数，和为 j ，构成的不同集合数。

枚举 i，j，再枚举 prime[i] 的幂次，转移。

注意对每个质数可以使用多次，lcm 都是不同的，这也就是需要枚举幂次的原因。如 $\{2,2,2,3,3\}\neq\{2,3\}$，且即使集合只包含单个质数，也可以使得lcm为集合所有元素的和，如 $\{2,2,2\}$，直接取 8，1，1.

#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define debug(x) cout<<#x<<":\t"<<x<<endl;
const int N = 2e6 + 10;
const int INF = 0x3f3f3f3f;
const ll inf = 0x3f3f3f3f3f3f3f3f;
const ll mod = 1e9 + 7;
int n, m;
int prime[N], vis[N], cnt;
void sieve(int n) {
	cnt = 0;
	for (int i = 2; i <= n; i++) {
		if (!vis[i]) {
			prime[++cnt] = i;
		}
		int d;
		for (int j = 1; j <= cnt && (d = i * prime[j]) <= n; j++) {
			vis[d] = 1;
			if (i%prime[j] == 0)break;
		}
	}
}
ll dp[1010][1010];
int main() {
	sieve(1000);
	scanf("%d", &n);
	dp[0][0] = 1;
	for (int i = 1; i <= cnt && prime[i] <= n; i++) {
		m++;
		for (int j = 0; j <= n; j++) {
			dp[i][j] = dp[i - 1][j];
			int x = prime[i];
			while (j - x >= 0) {
				dp[i][j] += dp[i - 1][j - x];
				x *= prime[i];
			}
		}
	}
	ll ans = 0;
	for (int i = 0; i <= n; i++)ans += dp[m][i];
	printf("%lld\n", ans);
	return 0;
}

 

[SDOI2012]LONGGE的问题

 

题意：求 $\sum_{i=1}^N \gcd(i,N)$，$1\le N\le 2^{32}$。

$$\begin{align} \sum_{i=1}^n\gcd(i,n) &= \sum_{d|n}d\cdot\sum_{i=1}^n[\gcd(i,n)=d]\\ &= \sum_{d|n}d\cdot\sum_{i=1}^{n/d}[\gcd(i,n/d)=1]\\ &= \sum_{d|n}d\cdot\varphi(n/d)\\ \end{align}$$

然而由于 n 太大，不能筛，但是由于只要求 n 的因数的 phi ，所以可以暴力求。

$O(\sqrt{n})$ 枚举 n 的因数，再 $O(n^{1/4})$ 枚举 质因子，求出 $\varphi=\prod (p^k-p^{k-1})$。

#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define debug(x) cout<<#x<<":\t"<<x<<endl;
const int N = 2e6 + 10;
const int INF = 0x3f3f3f3f;
const ll inf = 0x3f3f3f3f3f3f3f3f;
const ll mod = 1e9 + 7;
ll n;
ll phi(ll n) {
	ll res = 1;
	for (ll i = 2; i*i <= n; i++) {
		if (n%i)continue;
		ll tmp = 1;
		while (n%i == 0) {
			tmp *= i;
			n /= i;
		}
		res = res * (tmp - tmp / i);
	}
	if (n != 1)res = res * (n - 1);
	return res;
}
ll ans;
int main() {
	scanf("%lld", &n);
	for (ll i = 1; i*i <= n; i++) {
		if (n%i == 0) {
			ans += i * phi(n / i);
			if (n / i != i)ans += (n / i)*phi(i);
		}
	}
	printf("%lld\n", ans);
	return 0;
}

 

简单数据结构1

 

题意：给一个长为n的序列，m次操作，每次操作：1.区间 $[l,r]$ 加 $x$ ；2.对于区间 $[l,r]$ ，查询 $a[l]^{a[l+1]^{a[l+2]^{\cdots}}}$，一直到 $a[r]$ 。请注意每次的模数不同。

欧拉降幂

对一个数进行 $O(\log n)$ 次 $n=\varphi(n)$ 会变为 1。

所以只要当 $\varphi$ 变为 1 时结束，就可以 $O(\log n)$ dfs出结果。

但还有一个关键点。

注意到上面欧拉降幂的第三种情况会加 $\varphi(p)$，而在其他情况下不用加，这就导致我们没法直接取模。而应该用特殊的mod方法。

ll Mod(ll x, ll mod) {
	return x < mod ? x : (x % mod + mod);
}

模板里也有。

还需要区间加以及单点求值，可以用树状数组做差分。

还需要注意的是当 mod=1 时，要停止dfs，这时不能直接return 0，因为它的返回值可能要作为某个第三种情况的指数，此时 $p=2,\varphi(p)=1$，所以还是需要加 1，所以统一还是用Mod。

#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define debug(x) cout<<#x<<":\t"<<x<<endl;
const int N = 2e7 + 10;
const int INF = 0x3f3f3f3f;
const ll inf = 0x3f3f3f3f3f3f3f3f;
//const ll mod = 1e9 + 7;
int phi[N];
int prime[N], vis[N], cnt;
void sieve(int n) {
	cnt = 0;
	for (int i = 2; i <= n; i++) {
		if (!vis[i]) {
			prime[cnt++] = i;
			phi[i] = i - 1;
		}
		ll d;
		for (int j = 0; j < cnt && (d = i * prime[j]) <= n; j++) {
			vis[d] = 1;
			if (i%prime[j] == 0) {
				phi[d] = phi[i] * prime[j];
				break;
			}
			else {
				phi[d] = phi[i] * phi[prime[j]];
			}
		}
	}
}
ll Mod(ll x, ll y) {
	return x >= y ? (x%y + y) : x;
}
int n, q;
ll a[N];
ll sum[N];
void add(int q, ll x) {
	for (int i = q; i <= n; i += (i&-i))
		sum[i] += x;
}
ll qry(int r, ll mod) {
	ll res = 0;
	for (int i = r; i > 0; i -= (i&-i))
		res = Mod(res + sum[i],  mod);
	return res;
}

ll gcd(ll a, ll b) {
	if (a < b)swap(a, b);
	return b == 0 ? a : gcd(b, a%b);
}

ll Pow(ll a, ll b, ll mod) {
	ll res = 1ll;
	while (b) {
		if (b & 1)res = Mod(res * a, mod);
		a = Mod(a * a, mod);
		b >>= 1;
	}
	return res;
}
ll dfs(int l, int r, ll mod) {
	if (l == r || mod == 1) {
		return qry(l, mod);
	}
	ll t = qry(l, mod);
	if (gcd(t, mod) == 1) {
		return Pow(t, dfs(l + 1, r, phi[mod]), mod);
	}
	else {
		return Pow(t, dfs(l + 1, r, phi[mod]), mod);
	}
}
int main() {
	sieve(N - 1);
	scanf("%d%d", &n, &q);
	for (int i = 1; i <= n; i++)scanf("%lld", &a[i]);
	for (int i = 1; i <= n; i++) {
		add(i, a[i]);
		add(i + 1, -a[i]);
	}
	while (q--) {
		int op, l, r;
		ll p;
		scanf("%d%d%d%lld", &op, &l, &r, &p);
		if (op == 1) {
			add(l, p);
			add(r + 1, -p);
		}
		else {
			printf("%lld\n", dfs(l, r, p) % p);
		}
	}
	return 0;
}

 

[AHOI2013]找硬币

 

题意：要求构造出一些货币，满足任意两个成倍数关系，最小的面额是1，有 n 个物品，每个价格 $a[i]$，要用这些货币买这 n 个物品，且用的货币数量最少，问数量。

dp

$dp[i]$ 表示最大的面额为 $i$ 时，买下 n 个物品用的货币数量。

由于任意两个面额成倍，所以可以贪心，对于一串面额，必定是先用大的，再用小的。

这里的最大面额变大的意思是加入一个更大的面额，而不是替换。

当最大面额变大时，由于必然尽量多使用最大面额，所以可以算出原先使用旧的最大面额的数量以及新的最大面额的数量。

$dp[i*j]=min(dp[i*j],dp[i]-cnt)$

$cnt$ 表示使用 $i*j$ 作为新的最大面额，省下的货币数量。

#include <bits/stdc++.h>
using namespace std;
#define ll long long
const int N = 2e6 + 10;
const int INF = 0x3f3f3f3f;
const ll inf = 0x3f3f3f3f3f3f3f3f;
const ll mod = 998244353;
#define ull unsigned ll
#define debug(x) cout<<#x<<":\t"<<x<<endl;
int n, a[N], mx, ans;
int dp[N];
int main() {
	scanf("%d", &n);
	memset(dp, 0x3f, sizeof(dp));
	dp[1] = 0;
	for (int i = 1; i <= n; i++) {
		scanf("%d", &a[i]);
		dp[1] += a[i];
		mx = max(mx, a[i]);
	}
	ans = dp[1];
	for (int i = 1; i <= mx; i++) {
		for (int j = 2; j*i <= mx; j++) {
			int cnt = 0;
			for (int k = 1; k <= n; k++) {
				int c = a[k] / i;
				cnt += c / j * (j - 1);
			}
			dp[i*j] = min(dp[i*j], dp[i] - cnt);
			ans = min(ans, dp[i*j]);
		}
	}
	for (int i = 1; i <= mx; i++)ans = min(ans, dp[i]);
	printf("%d\n", ans);
	return 0;
}

 

小A与最大子段和

 

题意：给定一个数列 a，求一个非空连续子段 b，满足 $\sum_{i=1}^m b[i]\cdot i$ 最大。

斜率优化dp

直接用 b 的下标不好处理，考虑转换成 a 中的下标。并枚举子段的右端点。

设 $dp[i]$ 表示以 $i$ 为右端点的所有子段的最大的 $\sum_{i=1}^m b[i]\cdot i$。

$dp[i]=\max_{j=0}^{i-1}(f[i]-f[j]-j\cdot(sum[i]-sum[j]))$， $j$ 为子段左端点前一个位置。$f[i]=\sum_{j=1}^i a[j]\cdot j$，$sum[i]=\sum_{j=1}^i a[j]$。

对于两个点 $j>k$，$j$ 优于 $k$ 等价于

$$f[i]-f[j]-j\cdot(sum[i]-sum[j])>f[i]-f[k]-k\cdot(sum[i]-sum[k])\\$$

移项整理得到

$$\frac{(j\cdot sum[j]-f[j])-(k\cdot sum[k]-f[k])}{j-k}>sum[i]\\$$

典型的斜率优化dp

令 $g(i)=i\cdot sum[i]-f[i]$。则有

$$\frac{g(j)-g(k)}{j-k}>sum[i]\\$$

单调队列维护上凸包。队列中斜率递减。最优点左侧斜率大于 $sum[i]$，右侧斜率小于等于 $sum[i]$。

由于 $sum[i]$ 不单调（$a[i]$ 可能为负），所以不能直接每次都弹出队首取队首。而应该在队列中二分出最优点。

#include <bits/stdc++.h>
using namespace std;
#define ll long long
const int N = 2e6 + 10;
const int INF = 0x3f3f3f3f;
const ll inf = 0x3f3f3f3f3f3f3f3f;
const ll mod = 998244353;
#define ull unsigned ll
#define debug(x) cout<<#x<<":\t"<<x<<endl;
int n;
ll f[N], sum[N], a[N];
int l, r, q[N];
ll g(int x) {
	return x * sum[x] - f[x];
}
bool ck(ll x, int i) {
	return i == 1 || g(q[i]) - g(q[i - 1]) >= x*(q[i] - q[i - 1]);
}
ll ans = -inf;
int main() {
	scanf("%d", &n);
	for (int i = 1; i <= n; i++) {
		scanf("%lld", &a[i]);
		sum[i] = sum[i - 1] + a[i];
		f[i] = f[i - 1] + a[i] * i;
	}
	l = r = 1;		//队首放一个 0，因为 j 的范围从 0 到 n-1
	for (int i = 1; i <= n; i++) {
		int L = l, R = r;
		while (L < R) {
			int mid = (L + R + 1) / 2;
			if (ck(sum[i], mid))L = mid;
			else R = mid - 1;
		}
		ans = max(ans, f[i] - f[q[L]] - q[L] * (sum[i] - sum[q[L]]));
		while (r > l && (g(i) - g(q[r]))*(q[r] - q[r - 1]) >= (g(q[r]) - g(q[r - 1]))*(i - q[r])) {			//队列中至少要有一个数，r=l不能再弹了
			r--;
		}
		q[++r] = i;
	}
	printf("%lld\n", ans);
	return 0;
}

 

没有名字

 

题意：给定 n，m，k，求以下式子迭代 m 次后数组 $a[i]$ 值。$1\le n,k\le200,1\le m\le 10^{18}$

矩阵快速幂+循环矩阵

维护矩阵 $(a_1,a_2,\cdots,a_n)$，和相应系数矩阵。

矩阵快速幂需要 $n^3$，但是发现系数矩阵是个循环矩阵，由循环矩阵定义得到可以 $O(n^2)$ 求得，由循环矩阵性质得到循环矩阵乘积仍是循环矩阵。

#include <bits/stdc++.h>
#define debug(x) cout << #x << ":\t" << (x) << endl;
using namespace std;
#define ll long long
const int N = 2e6 + 10;
const int INF = 0x3f3f3f3f;
const ll inf = 0x3f3f3f3f3f3f3f3f;
const ll mod = 1e9 + 7;
struct Mat {
	ll a[210][210];
	int r, c;
	Mat(int _r, int _c) { r = _r, c = _c, memset(a, 0, sizeof(a)); }
	void init() { memset(a, 0, sizeof(a)); }
};
Mat operator * (Mat X, Mat Y) {
	Mat Z(X.r, Y.c);
	for (int i = 0; i < X.r; ++i) {
		for (int j = 0; j < Y.c; ++j) {
			for (int k = 0; k < X.c; ++k) {
				Z.a[i][j] = (Z.a[i][j] + 1ll * X.a[i][k] * Y.a[k][j] % mod) % mod;
			}
		}
	}
	return Z;
}
Mat mul(Mat X, Mat Y) {
	Mat Z(X.r, Y.c);
	for (int i = 0; i < Y.c; i++) {
		for (int j = 0; j < X.c; j++) {
			Z.a[0][i] = (Z.a[0][i] + 1ll * X.a[0][j] * Y.a[j][i] % mod) % mod;
		}
	}
	for (int i = 1; i < X.r; i++) {
		for (int j = 0; j < Y.c; j++) {
			Z.a[i][j] = Z.a[i - 1][(j - 1 + Y.c) % Y.c];
		}
	}
	return Z;
}
Mat pow(Mat a, ll n) {
	Mat res(a.r, a.c);
	for (int i = 0; i < a.r; i++)
		res.a[i][i] = 1;
	while (n) {
		if (n & 1) res = mul(res, a);
		a = mul(a, a);
		n >>= 1;
	}
	return res;
}
int T;
int n, k; ll m;
int main() {
	scanf("%d", &T);
	while (T--) {
		scanf("%d%lld%d", &n, &m, &k);
		Mat A(n, 1), B(n, n);
		for (int i = 0; i < n; i++)scanf("%lld", &A.a[i][0]);
		for (int i = 0; i < n; i++) {
			for (int j = 0; j < n; j++) {
				int dis = min(abs(i - j), n - abs(i - j));
				if (i == j)B.a[i][j] = 0;
				else B.a[i][j] = max(0, k - dis);
			}
		}
		B = pow(B, m);
		A = B * A;
		for (int i = 0; i < n; i++)printf("%lld%c", A.a[i][0], " \n"[i == n - 1]);
	}
	return 0;
}