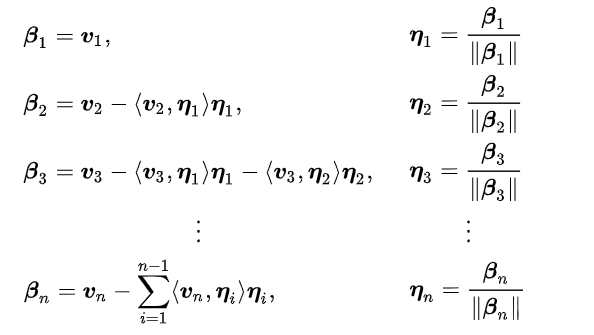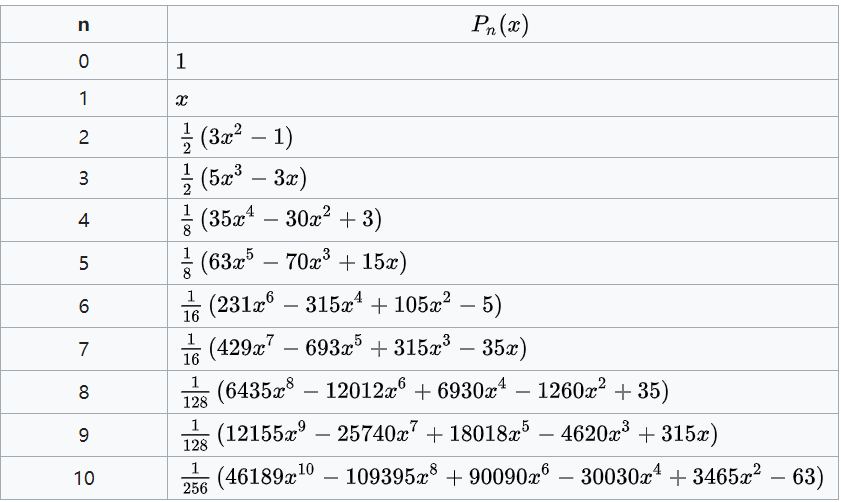overfit

L2正则化

• 目的：从高维降到低维，以降低$overfitting$的可能。
• 方法：从所有 $\sum_{q=0}^Q w_q^2\leq C$即$||w||^{2}\leq{c}$的$w$中选$Error$最小者。
• L2正则化后的$w$ 可能为0的项个数较少，但总的长度固定。

即满足$w$ 在半径为$\sqrt{c}$ 的球内。由于要使$w$ 最终达到$w_{lin}$ ，$w_{lin}$常常在某凸多边形的中心。

类似如图情况：

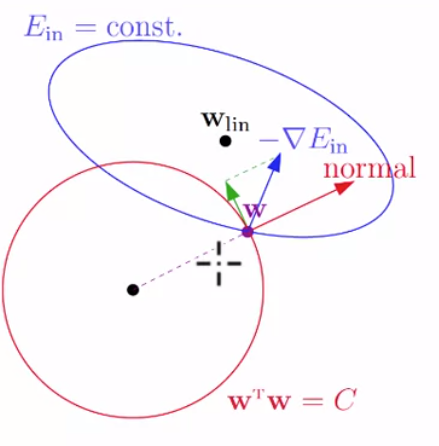
即所求极值点常在球面上，故可将条件 $||w||^{2}\leq{c}$变为$||w||^{2}={c}$

拉格朗日乘数法

问题转化为求$f(w)=E_{in}$在$g(w)=w^2-C=0$ 的条件下的条件极值。

拉格朗日乘数法将求 $f(w)$在$w$ 满足一定条件下的极值问题转化为求$F(w)$ 在无约束条件下的极值。

$$F(w,\lambda)=f(w)+\lambda g(w)$$

$||w||^{2}\leq{c}$ 同样可写为$\sum_{q=0}^Q \lambda w_q^2 \leq 1$

其中$\lambda \propto \frac{1}{C}$，即$\lambda$ 越大，C越小，对$w$ 的筛选作用越大。

接着就可以用regression方法逼近。

证明：

假设点$(x,y)$满足$\left\{ \begin{aligned} f(x,y)&=k,(k为f极值) \\ g(x,y)&=0 \end{aligned} \right.$，则

$$\left\{ \begin{aligned} {\rm d}f(x,y)&=\frac{\partial f}{\partial x}{\rm d}x+\frac{\partial f}{\partial y}{\rm d}y=0 \\ {\rm d}g(x,y)&=\frac{\partial g}{\partial x}{\rm d}x+\frac{\partial g}{\partial y}{\rm d}y=0 \end{aligned} \right.$$

$$\Downarrow$$

$$\frac{\frac{\partial f}{\partial x}}{\frac{\partial g}{\partial x}}=\frac{\frac{\partial f}{\partial y}}{\frac{\partial g}{\partial y}}=-\lambda$$

即

$$\left\{ \begin{aligned} \frac{\partial f}{\partial x}+\lambda \frac{\partial g}{\partial x}&=0\\ \frac{\partial f}{\partial y}+\lambda \frac{\partial g}{\partial y}&=0 \end{aligned} \right.$$

全微分积分得

$$L(x,y,\lambda)=f(x,y)+\lambda g(x,y)$$

勒让德多项式

定义在$\langle p,q\rangle=\int_{-1}^1 p(x)q(x)$ 内积上的正交多项式

在 $|x|<1$时，会造成w变大。

将x正交化。

$$(1,x,x^2,x^3,\cdots,x^Q)\Rightarrow(1,x,\frac{1}{2}(3x^2-1),\frac{1}{2}(5x^3-3x),\cdots)$$

箭头右边的就是勒让德多项式，这是一系列两两正交的向量。

而推导勒让德多项式的一种方法就是对$(1,x,x^2,\cdots)$ Gram-Schmidt正交化。

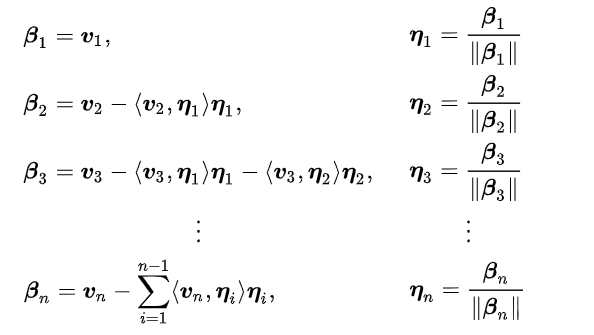
一部分勒让德多项式：

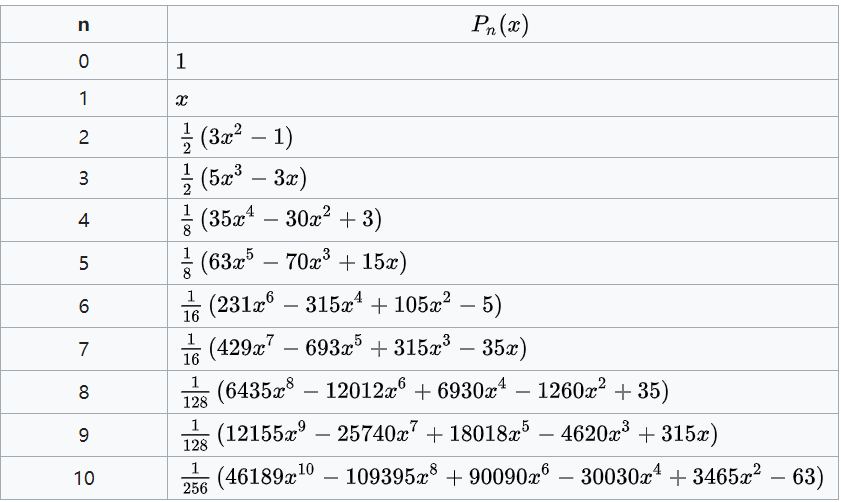
更多正交多项式见https://blog.zmyme.com/archives/118

L1正则化

• 取$\sum w_i=C$ 的 $w$

• 用于快速取得结果，因为满足条件的$w$必定有规定个数的项为 0 .

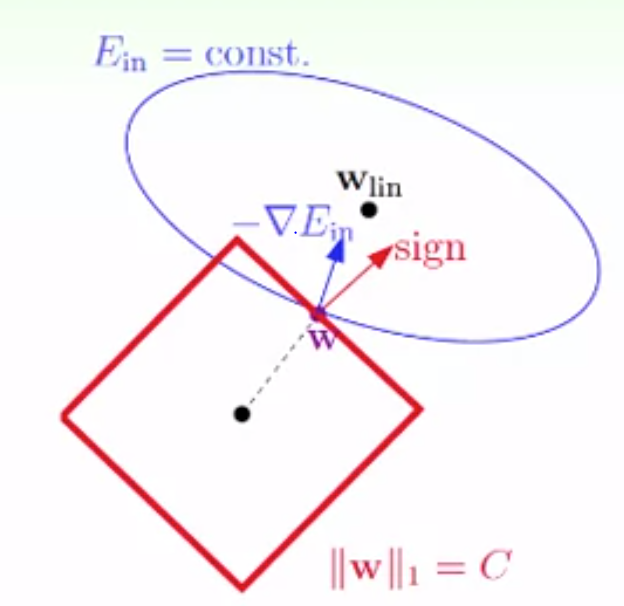
对L1与L2正则化，nosie越多，次数越大，$\lambda$ 越大。