https://atcoder.jp/contests/abc168/tasks
E - ∙ (Bullet)
题意:有n个物品,每个物品都有Ai,Bi两个值,选出一个非空子集,且满足子集中不存在两个物品的 Ai⋅Aj+Bi⋅Bj=0,问有多少种选择方式。
思路比较简单,式子移项得到 BiAi=−AjBj,所以维护每个物品的 BiAi,最后计数即可。
但是写起来还是有技巧的。
首先要考虑分母为零,还要考虑精度。
所以可以考虑不除过去,而是直接维护 (Ai,Bi),对应 (−Bi,Ai),把这两类合并为一类,并用 (Ai,Bi),Ai>0,Bi≥0 表示,并用pair表示原先实际的两类各自的个数。
注意类的second始终要为非负数,且first始终要为正数,所以当 Ai=0 时,要注意放到第二类去。
还有一种是 Ai=Bi=0,要选这些数只能单独选,不能和任何物品放一起。
然后枚举每一类,按照选/不选计数。
当然也可以直接维护分数,但是要给分母为零的情况单独开一个,并且不能重复枚举。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
| #include <bits/stdc++.h>
using namespace std;
#define ll long long
const int N = 2e5 + 10;
const int INF = 0x3f3f3f3f;
const ll inf = 0x3f3f3f3f3f3f3f3f;
const ll mod = 1000000007;
const ll inv2 = (mod + 1) / 2;
int n;
ll a, b;
ll c0, ans = 1;
typedef pair<ll, ll>pii;
map<pii, pii>mp;
ll Pow(ll a, ll b) {
ll res = 1ll;
while (b) {
if (b & 1)res = res * a%mod;
a = a * a%mod;
b >>= 1;
}
return res;
}
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; i++) {
scanf("%lld%lld", &a, &b);
if (a == 0 && b == 0)c0++;
else {
if (b < 0)a = -a, b = -b;
ll g = abs(gcd(a, b));
a /= g; b /= g;
if (a > 0)mp[pii(a, b)].first++;
else mp[pii(b, -a)].second++;
}
}
for (auto p : mp) {
ll tmp = (Pow(2, p.second.first) + Pow(2, p.second.second) + mod - 1) % mod;
ans = ans * tmp%mod;
}
printf("%lld\n", (ans + mod - 1 + c0) % mod);
return 0;
}
|
F - . (Single Dot)
题意:二维平面上一个初始点,给出一些水平和垂直的线段,从初始点出发,不能穿过线段,问能走的面积。
挺恶心的一道题。
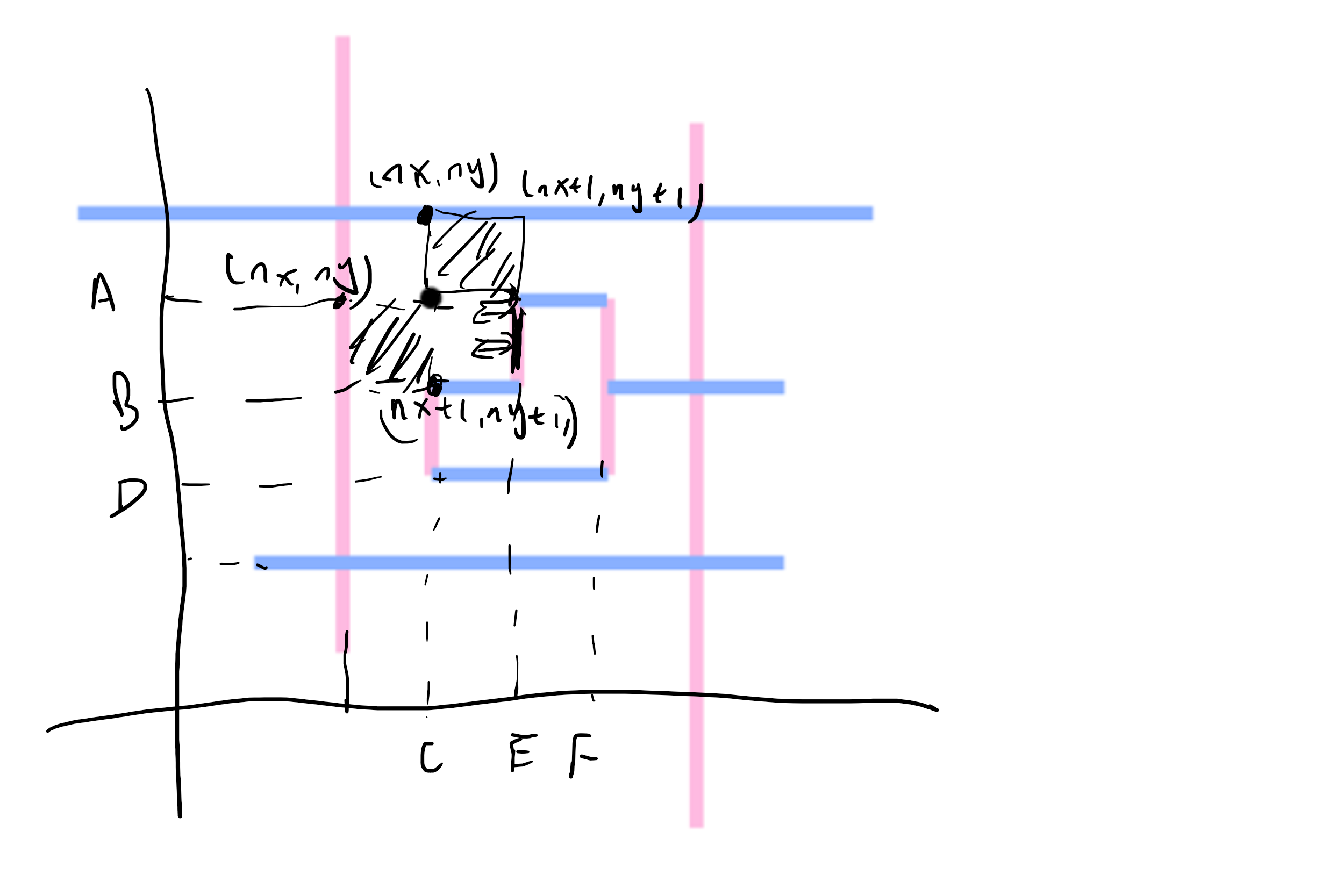
考虑枚举点,点之间构成矩形,一个个小矩形组成最终面积,但是看到点的范围显然不能枚举点,所以要先离散化。
然后从初始点开始,往外bfs,找到能到达的点,并得到新的小矩形。
但是如果新的点在线段上,则不能计入,但是要规定只有不能从左或从上到达线段,也不能从线段上向右或向下走。因为如果限制四个方向都不能走,会少掉一块矩形。
插入左右上下无穷大处的坐标,判断如果能到达,则面积无穷大。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
| #include<bits/stdc++.h>
using namespace std;
#define ll long long
const int INF = 0x3f3f3f3f;
const int N = 3e3 + 10;
int n, m;
int A[N], B[N], C[N], D[N], E[N], F[N];
ll ans;
vector<int>xx, yy;
int id(vector<int>&vc, int x) {
return lower_bound(vc.begin(), vc.end(), x) - vc.begin();
}
int dx[]{ 0,0,-1,1 };
int dy[]{ -1,1,0,0 };
int die[N][N][4];
typedef pair<int, int> pii;
queue<pii>q;
int vis[N][N];
int main() {
scanf("%d%d", &n, &m);
xx.push_back(0);
yy.push_back(0);
xx.push_back(-INF); xx.push_back(INF);
yy.push_back(-INF); yy.push_back(INF);
for (int i = 1; i <= n; i++) {
scanf("%d%d%d", &A[i], &B[i], &C[i]);
xx.push_back(A[i]);
xx.push_back(B[i]);
yy.push_back(C[i]);
}
for (int i = 1; i <= m; i++) {
scanf("%d%d%d", &D[i], &E[i], &F[i]);
yy.push_back(E[i]);
yy.push_back(F[i]);
xx.push_back(D[i]);
}
sort(xx.begin(), xx.end()); xx.erase(unique(xx.begin(), xx.end()), xx.end());
sort(yy.begin(), yy.end()); yy.erase(unique(yy.begin(), yy.end()), yy.end());
for (int i = 1; i <= n; i++) {
A[i] = id(xx, A[i]);
B[i] = id(xx, B[i]);
C[i] = id(yy, C[i]);
for (int j = A[i]; j < B[i]; j++) {
die[j][C[i]][0] = 1;
die[j][C[i] - 1][1] = 1;
}
}
for (int i = 1; i <= m; i++) {
D[i] = id(xx, D[i]);
E[i] = id(yy, E[i]);
F[i] = id(yy, F[i]);
for (int j = E[i]; j < F[i]; j++) {
die[D[i]][j][2] = 1;
die[D[i] - 1][j][3] = 1;
}
}
q.push(pii(id(xx, 0), id(yy, 0)));
while (!q.empty()) {
int x = q.front().first, y = q.front().second; q.pop();
if (vis[x][y])continue;
if (x == 0 || x == (int)xx.size() - 1 || y == 0 || y == (int)yy.size() - 1) {
puts("INF");
return 0;
}
ans += 1ll * (xx[x + 1] - xx[x])*(yy[y + 1] - yy[y]);
vis[x][y] = 1;
for (int i = 0; i < 4; i++) {
if (die[x][y][i])continue;
int nx = x + dx[i], ny = y + dy[i];
q.push(pii(nx, ny));
}
}
printf("%lld\n", ans);
return 0;
}
|







