https://acm.ecnu.edu.cn/contest/362/

A. 棋局

 

题意：在一个 n∗mn*m，1≤n,m≤101\le n,m\le 10 的棋盘上，每格有 a[i][j]a[i][j] 和 b[i][j]b[i][j]，两人轮流下棋，仅当该位置没有棋子且该位置左侧和上方所有格子内都有棋子，才可以在该位置落子。最终，先手方的分数为占有的格子的 aa 值之和，后手方的分数为占有的格子的 bb 值之和，问双方都最优的情况下最终先手方与后手方的分数差。

MinMax博弈+哈希/轮廓线dp

两种做法。

第一种 哈希。

本题最关键的一点是，由于落子的格子必须上方和左方都放满了，所以棋盘上一定是每一行的棋子数递增，第一行最多，第二行其次，以此类推。且每一行都是放满了一个前缀。

这就限制了实际上可行的状态数非常少，少到可以直接暴力dfs枚举。

数组 p[i]p[i] 记录下第 ii 行有几个棋子，哈希存起来，dfs。

本来MinMax是要分当前是先手方还是后手方讨论的，但是因为这里只要求差值，所以换了一个人操作，他与对方的差值恰好是对方与他的差值的相反数，直接减去即可，就不需要讨论了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
#include <bits/stdc++.h>
#define debug(x) cout << #x << ":\t" << (x) << endl;
using namespace std;
#define ll long long
#define ull unsigned ll
const int N = 2e6 + 10;
const int INF = 0x3f3f3f3f;
const ll inf = 0x3f3f3f3f3f3f3f3f;
const ll mod = 1e9 + 7;
const ll inv2 = (mod + 1) / 2;
int n, m;
int a[20][20], b[20][20], p[20];
ll ed;
unordered_map<ll, ll>dp;
ll hsh() {
	ll ans = 0;
	for (int i = 1; i <= n; i++)ans = ans * mod + p[i];
	return ans;
}
ll dfs(ll s, int flg) {
	if (s == ed)return 0;
	if (dp.count(s))return dp[s];
	ll ans = -inf;
	for (int i = 1; i <= n; i++) {
		if (p[i] < m && (i == 1 || p[i] < p[i - 1])) {
			p[i]++;
			ans = max(ans, (flg ? a[i][p[i]] : b[i][p[i]]) - dfs(hsh(), !flg));
			p[i]--;
		}
	}
	return dp[s] = ans;
}
int main() {
	scanf("%d%d", &n, &m);
	for (int i = 1; i <= n; i++)for (int j = 1; j <= m; j++)scanf("%d", &a[i][j]);
	for (int i = 1; i <= n; i++)for (int j = 1; j <= m; j++)scanf("%d", &b[i][j]);
	for (int i = 1; i <= n; i++)ed = ed * mod + m;
	printf("%lld\n", dfs(0, 1));
	return 0;
}

 

第二种 轮廓线dp。

同样是dfs，可以发现每次dfs的时候只需要直到各行都放了几个，由于一定都是挤在一起的，所以只要知道了轮廓线，就能转移，轮廓线相同则状态也相同。所以可以进行轮廓线dp。

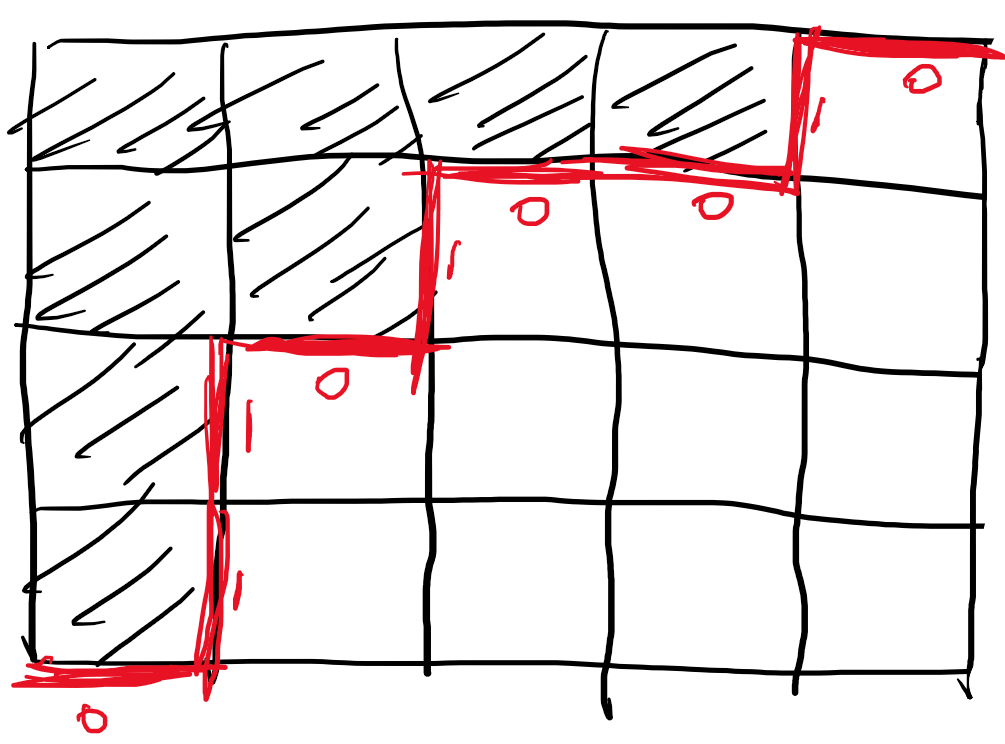
如上图，假设阴影格子是已经放了棋子，不用管是谁放的（这也是可以轮廓线dp的原因）。

红线是轮廓线，用 0 表示横线，1 表示竖线。

则上图的状态可以用 011010010 表示（从左到右）。

则一个合法的落子位置一定是左边有 1，上边有 0，也就是连续的 10 处。

而在放下棋子后，就会从 10 变成 01，所以转移到的新状态也就可以得到了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
#include <bits/stdc++.h>
#define debug(x) cout << #x << ":\t" << (x) << endl;
using namespace std;
#define ll long long
#define ull unsigned ll
const int N = 2e6 + 10;
const int INF = 0x3f3f3f3f;
const ll inf = 0x3f3f3f3f3f3f3f3f;
const ll mod = 1e9 + 7;
const ll inv2 = (mod + 1) / 2;
int n, m;
int a[20][20], b[20][20], ed;
unordered_map<int, ll>dp;
ll dfs(int s, int flg) {
	if (s == ed)return 0;
	if (dp.count(s))return dp[s];
	int x = 0, y = m;
	ll ans = -inf;
	for (int i = 0; i < n + m; i++) {
		if (s >> i & 1)x++;
		else y--;
		if ((s >> i & 3) != 2)continue;
		ans = max(ans, (flg ? a[x][y] : b[x][y]) - dfs(s ^ (3 << i), !flg));
	}
	return dp[s] = ans;
}
int main() {
	scanf("%d%d", &n, &m);
	for (int i = 0; i < n; i++)for (int j = 0; j < m; j++)scanf("%d", &a[i][j]);
	for (int i = 0; i < n; i++)for (int j = 0; j < m; j++)scanf("%d", &b[i][j]);
	ed = (1 << n) - 1;
	int s = (((1 << (n + m)) - 1) ^ ((1 << m) - 1));
	printf("%lld\n", dfs(s, 1));
	return 0;
}

 

E. 农场规划

 

题意：给定一张无向图。要求删掉最少的边，使得每个编号小于等于 kk 的节点都不在环里。

画几个例子，就能直接猜只要遇到了环，无论删哪条边，答案都是一样的。

那么就直接并查集加边的同时判环。

所以问题只剩下怎么找到所有涉及的环因为所有涉及的环必定有边的端点包含小于等于 k 的节点，而像上面说的，环里无论删哪条边都一样，那么就删这些包含小于等于 k 的节点的边。

并且每加入一条含特殊点的边，最多只会多出一个含特殊点的环（只要之前没有含特殊点的环），所以可以放心乱搞。

所以先把不含特殊点的边都加进图里，再加含特殊点的边，在这时再判环。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
#include <bits/stdc++.h>
#define debug(x) cout << #x << ":\t" << (x) << endl;
using namespace std;
#define ll long long
#define ull unsigned ll
const int N = 2e6 + 10;
const int INF = 0x3f3f3f3f;
const ll inf = 0x3f3f3f3f3f3f3f3f;
const ll mod = 1e9 + 7;
const ll inv2 = (mod + 1) / 2;
int n, m, k;
struct E
{
	int u, v;
};
vector<E>es;
int par[N];
int find(int x) { return par[x] == x ? x : par[x] = find(par[x]); }
void unit(int x, int y) { par[find(x)] = find(y); }
int main() {
	scanf("%d%d%d", &n, &m, &k);
	for (int i = 1; i <= n; i++)par[i] = i;
	int ans = 0;
	for (int i = 1; i <= m; i++) {
		int u, v;
		scanf("%d%d", &u, &v);
		if (min(u, v) <= k)es.push_back({ u,v });
		else unit(u, v);
	}
	for (E& e : es) {
		int u = e.u, v = e.v;
		if (find(u) == find(v))ans++;
		else unit(u, v);
	}
	printf("%d\n", ans);
	return 0;
}

 

D. 匿名信

 

题意：给定 NN 个模式串，以及一个文本串，每个模式串有代价，问用模式串拼出文本串的最小代价。

AC自动机+dp

在AC自动机上跳fail链，更新dp。

但这样有个问题，比如 模式串aaaaaaa，构建出的fail链是每一个节点指向它的父亲。但是更新dp的时候只有在存储了完整串的节点上才能更新，所以这样跳fail会一直向上跳都是没有意义的。

所以需要再来一个lst指针，指向存储了完整串的fail节点。在更新dp的时候跳lst链，在其他地方跳的时候还是跳fail。（空儿子还是指向fail的儿子）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
#include <bits/stdc++.h>
#define debug(x) cout << #x << ":\t" << (x) << endl;
using namespace std;
#define ll long long
#define ull unsigned ll
const int N = 2e6 + 10;
const int INF = 0x3f3f3f3f;
const ll inf = 0x3f3f3f3f3f3f3f3f;
const ll mod = 1e9 + 7;
const ll inv2 = (mod + 1) / 2;
int tr[N][26], tot;
ll e[N]; int fail[N], dep[N], lst[N];
void insert(char *s, ll p) {
	int u = 0;
	for (int i = 0; s[i]; i++) {
		if (!tr[u][s[i] - 'a']) tr[u][s[i] - 'a'] = ++tot;
		u = tr[u][s[i] - 'a'];
	}
	e[u] = min(e[u], p);
	dep[u] = (int)strlen(s);
}
queue<int> q;
void build() {
	for (int i = 0; i < 26; i++)
		if (tr[0][i]) q.push(tr[0][i]);
	while (q.size()) {
		int u = q.front();
		q.pop();
		for (int i = 0; i < 26; i++) {
			if (tr[u][i]) {
				fail[tr[u][i]] = tr[fail[u]][i];
				q.push(tr[u][i]);
				lst[tr[u][i]] = (e[fail[tr[u][i]]] != inf ? fail[tr[u][i]] : lst[fail[tr[u][i]]]);
			}
			else
				tr[u][i] = tr[fail[u]][i];
		}
	}
}
int m, n;
char s[N];
ll dp[N];
int main() {
	scanf("%d", &m);
	memset(e, 0x3f, sizeof(e));
	for (int i = 0; i < m; i++) {
		ll p;
		scanf("%s%lld", s, &p);
		insert(s, p);
	}
	build();
	scanf("%s", s + 1);
	n = (int)strlen(s + 1);
	memset(dp, 0x3f, sizeof(dp));
	dp[0] = 0;
	e[0] = 0;
	int u = 0;
	for (int i = 1; i <= n; i++) {
		u = tr[u][s[i] - 'a'];
		for (int j = u; j; j = lst[j]) {
			dp[i] = min(dp[i], dp[i - dep[j]] + e[j]);
		}
	}
	printf("%lld\n", dp[n] == inf ? -1 : dp[n]);
	return 0;
}