https://ac.nowcoder.com/acm/contest/10845
E - 牛牛数数
题意:给定 n 个数字,用其中任意一个非空子集的异或和得到数字 x,问有多少种 x 大于给定数 K。
线性基+二分
线性基求第 k 大模板。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 #include <bits/stdc++.h> #define debug(x) cout << #x << ":\t" << (x) << endl; using namespace std;#define ll long long #define ull unsigned ll const int N = 2e6 + 10 ;const int INF = 0x3f3f3f3f ;const ll inf = 0x3f3f3f3f3f3f3f3f ;const ll mod = 1e9 + 7 ;const ll inv2 = (mod + 1 ) / 2 ;struct Linear_Basis { ll b[63 ], nb[63 ], tot, len; void init () { tot = 0 ; len = 0 ; memset (b, 0 , sizeof memset (nb, 0 , sizeof } bool ins (ll x) { for (int i = 62 ; i >= 0 ; i--) if (x&(1ll << i)) { if (!b[i]) { b[i] = x; len++; break ; } x ^= b[i]; } return x > 0 ; } ll Max () { ll res = 0 ; for (int i = 62 ; i >= 0 ; i--) res = max (res, res^b[i]); return res; } ll Min () { for (int i = 0 ; i <= 62 ; i++) if (b[i]) return b[i]; return -1 ; } void rebuild () { tot = 0 ; for (int i = 62 ; i >= 0 ; i--) for (int j = i - 1 ; j >= 0 ; j--) if (b[i] & (1ll << j)) b[i] ^= b[j]; for (int i = 0 ; i <= 62 ; i++) if (b[i]) nb[tot++] = b[i]; } ll Kth_Max (ll k) { ll res = 0 ; for (int i = 62 ; i >= 0 ; i--) if (k&(1ll << i)) res ^= nb[i]; return res; } } LB; int n;ll K; ll a[N]; int main () scanf ("%d%lld" , &n, &K); for (int i = 1 ; i <= n; i++) { scanf ("%lld" , &a[i]); LB.ins (a[i]); } ll mx = LB.Max (); ll mn = LB.Min (); if (mx <= K) { puts ("0" ); return 0 ; } if (mn > K) { printf ("%lld\n" , n); return 0 ; } ll L = 1 , R = (1ll << LB.len); LB.rebuild (); while (L < R) { ll mid = (L + R + 1 ) / 2 ; ll x = LB.Kth_Max (mid); if (x <= K)L = mid; else R = mid - 1 ; } printf ("%lld\n" , (1ll << LB.len) - 1 - L); return 0 ; }
F - phi and phi
题意:定义 ans(n)=\sum_\limits{i=1}^n\sum\limits_{j=1}^n\phi(ij)\phi(\gcd(i,j))。给定 N N N a n s ( 1 ) , a n s ( 2 ) , ⋯ , a n s ( N ) ans(1),ans(2),\cdots,ans(N) an s ( 1 ) , an s ( 2 ) , ⋯ , an s ( N )
莫比乌斯反演+差分前缀和
ϕ ( n ) = n ⋅ ( 1 − 1 p 1 ) ( 1 − 1 p 2 ) ⋯ ( 1 − 1 p k ) \phi(n)=n\cdot(1-\frac{1}{p_1})(1-\frac{1}{p_2})\cdots(1-\frac{1}{p_k})\\
ϕ ( n ) = n ⋅ ( 1 − p 1 1 ) ( 1 − p 2 1 ) ⋯ ( 1 − p k 1 )
所以展开能得到
ϕ ( i j ) = ϕ ( i ) ϕ ( j ) ϕ ( gcd ( i , j ) ) ⋅ gcd ( i , j ) \phi(ij)=\frac{\phi(i)\phi(j)}{\phi(\gcd(i,j))}\cdot\gcd(i,j)\\
ϕ ( ij ) = ϕ ( g cd( i , j )) ϕ ( i ) ϕ ( j ) ⋅ g cd( i , j )
则
∑ i = 1 n ∑ j = 1 n ϕ ( i j ) ϕ ( gcd ( i , j ) ) = ∑ i = 1 n ∑ j = 1 n ϕ ( i ) ϕ ( j ) gcd ( i , j ) = ∑ d = 1 n d ∑ i = 1 n / d ∑ j = 1 n / d ϕ ( i d ) ϕ ( j d ) [ gcd ( i , j ) = 1 ] = ∑ d = 1 n d ∑ i = 1 n / d ∑ j = 1 n / d ϕ ( i d ) ϕ ( j d ) ∑ k ∣ gcd ( i , j ) μ ( k ) = ∑ d = 1 n d ∑ k = 1 n / d μ ( k ) ∑ i = 1 n / ( d ⋅ k ) ∑ j = 1 n / ( d ⋅ k ) ϕ ( i d k ) ϕ ( j d k ) = ∑ d = 1 n d ∑ k = 1 n / d μ ( k ) ( ∑ i = 1 n / ( d ⋅ k ) ϕ ( i d k ) ) 2 \begin{align}
&\sum_{i=1}^n\sum_{j=1}^n\phi(ij)\phi(\gcd(i,j))\\
&=\sum_{i=1}^n\sum_{j=1}^n\phi(i)\phi(j)\gcd(i,j)\\
&=\sum_{d=1}^n d\sum_{i=1}^{n/d}\sum_{j=1}^{n/d}\phi(id)\phi(jd)[\gcd(i,j)=1]\\
&=\sum_{d=1}^n d\sum_{i=1}^{n/d}\sum_{j=1}^{n/d}\phi(id)\phi(jd)\sum_{k|\gcd(i,j)}\mu(k)\\
&=\sum_{d=1}^n d\sum_{k=1}^{n/d}\mu(k)\sum_{i=1}^{n/(d\cdot k)}\sum_{j=1}^{n/(d\cdot k)}\phi(idk)\phi(jdk)\\
&=\sum_{d=1}^n d\sum_{k=1}^{n/d}\mu(k)(\sum_{i=1}^{n/(d\cdot k)}\phi(idk))^2\\
\end{align}
i = 1 ∑ n j = 1 ∑ n ϕ ( ij ) ϕ ( g cd( i , j )) = i = 1 ∑ n j = 1 ∑ n ϕ ( i ) ϕ ( j ) g cd( i , j ) = d = 1 ∑ n d i = 1 ∑ n / d j = 1 ∑ n / d ϕ ( i d ) ϕ ( j d ) [ g cd( i , j ) = 1 ] = d = 1 ∑ n d i = 1 ∑ n / d j = 1 ∑ n / d ϕ ( i d ) ϕ ( j d ) k ∣ g c d ( i , j ) ∑ μ ( k ) = d = 1 ∑ n d k = 1 ∑ n / d μ ( k ) i = 1 ∑ n / ( d ⋅ k ) j = 1 ∑ n / ( d ⋅ k ) ϕ ( i d k ) ϕ ( j d k ) = d = 1 ∑ n d k = 1 ∑ n / d μ ( k ) ( i = 1 ∑ n / ( d ⋅ k ) ϕ ( i d k ) ) 2
设 T = d ⋅ k T=d\cdot k T = d ⋅ k ( d , k ) (d,k) ( d , k ) ( T , d ) (T,d) ( T , d )
= ∑ T = 1 n ∑ d ∣ T d ⋅ μ ( T d ) ( ∑ i = 1 n / T ϕ ( i ⋅ T ) ) 2 \begin{align}
&=\sum_{T=1}^n\sum_{d|T}d\cdot\mu(\frac{T}{d})(\sum_{i=1}^{n/T}\phi(i\cdot T))^2\\
\end{align}
= T = 1 ∑ n d ∣ T ∑ d ⋅ μ ( d T ) ( i = 1 ∑ n / T ϕ ( i ⋅ T ) ) 2
由于有迪利克雷卷积公式 ϕ = I D ∗ μ \phi=ID*\mu ϕ = I D ∗ μ
= ∑ T = 1 n μ ( T ) ( ∑ i = 1 n / T ϕ ( i ⋅ T ) ) 2 =\sum_{T=1}^{n}\mu(T)(\sum_{i=1}^{n/T}\phi(i\cdot T))^2\\
= T = 1 ∑ n μ ( T ) ( i = 1 ∑ n / T ϕ ( i ⋅ T ) ) 2
换一下符号看得清楚点
最终
a n s ( n ) = ∑ d = 1 n μ ( d ) ( ∑ i = 1 n / d ϕ ( i ⋅ d ) ) 2 ans(n)=\sum_{d=1}^{n}\mu(d)(\sum_{i=1}^{n/d}\phi(i\cdot d))^2\\
an s ( n ) = d = 1 ∑ n μ ( d ) ( i = 1 ∑ n / d ϕ ( i ⋅ d ) ) 2
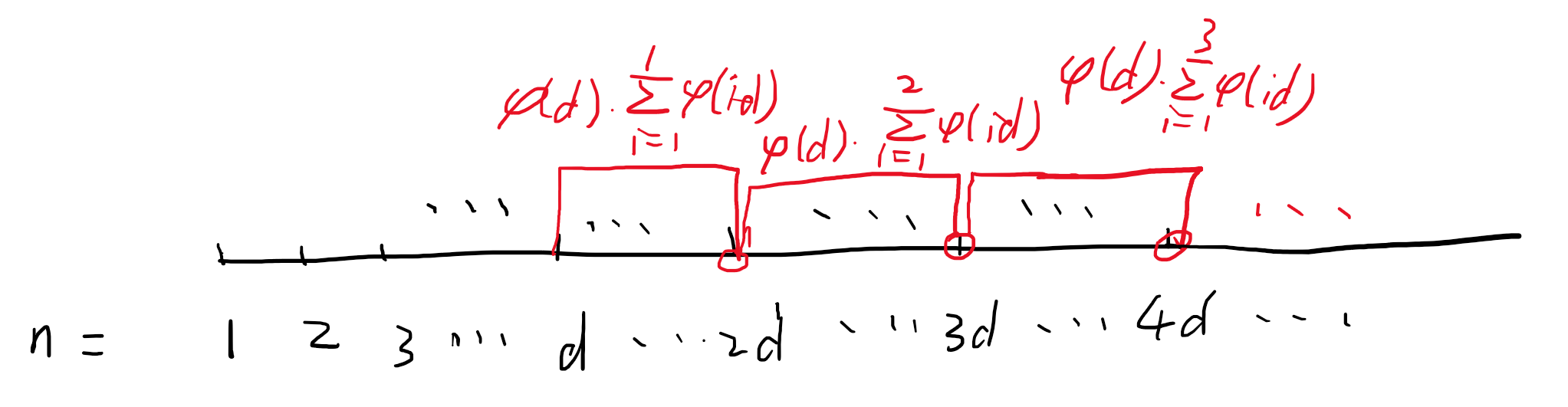
接下来枚举 d d d
在固定 d d d d d d n n n
对每个区间的贡献相同,所以差分做。
其中有 O ( n / d ) O(n/d) O ( n / d ) d d d 1 1 1 n n n O ( n log n ) O(n\log n) O ( n log n )
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 #include <bits/stdc++.h> #define debug(x) cout << #x << ":\t" << (x) << endl; using namespace std;#define ll long long #define ull unsigned ll const int N = 2e6 + 10 ;const int INF = 0x3f3f3f3f ;const ll inf = 0x3f3f3f3f3f3f3f3f ;const ll mod = 1e9 + 7 ;const ll inv2 = (mod + 1 ) / 2 ;int n;int prime[N], vis[N], tot, phi[N];void pre (int n) phi[1 ] = 1 ; for (int i = 2 ; i <= n; i++) { if (!vis[i]) { prime[tot++] = i; phi[i] = i - 1 ; } ll d; for (int j = 0 ; j < tot && (d = i * prime[j]) <= n; j++) { vis[d] = 1 ; if (i%prime[j] == 0 ) { phi[d] = phi[i] * prime[j]; break ; } else phi[d] = phi[i] * phi[prime[j]]; } } } ll ans[N]; int main () scanf ("%d" , &n); pre (n); for (int d = 1 ; d <= n; d++) { ll sum = 0 ; for (int i = 1 ; i <= n / d; i++) { sum = (sum + phi[i*d]) % mod; int L = i * d, R = min ((i + 1 )*d, n + 1 ); ans[L] = (ans[L] + sum * sum%mod*phi[d] % mod) % mod; ans[R] = (ans[R] - sum * sum%mod*phi[d] % mod + mod) % mod; } } for (int i = 2 ; i <= n; i++)ans[i] = (ans[i] + ans[i - 1 ]) % mod; for (int i = 1 ; i <= n; i++)printf ("%lld\n" , ans[i]); return 0 ; }
D - 魔物消灭计划
题意:给定一张带边权的无向图,一些点上有宝石,共有 k 种宝石,有相同宝石的点之间可以无代价传送,否则走相邻点,代价为边权。现在要使得起点 x,终点 y,以及一个至少包含 k 种宝石的点集连通,问最小代价。
斯坦纳树
比较模板的斯坦纳树题。
需要注意的是相同颜色的点要特殊处理,要么连成边权为零的团,要么求spfa的时候单独处理。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 #include <bits/stdc++.h> #define debug(x) cout << #x << ":\t" << (x) << endl; using namespace std;#define ll long long #define ull unsigned ll const int N = 2e6 + 10 ;const int INF = 0x3f3f3f3f ;const ll inf = 0x3f3f3f3f3f3f3f3f ;const ll mod = 1e9 + 7 ;const ll inv2 = (mod + 1 ) / 2 ;int n, m, k, x, y;struct E { int v, w; }; vector<E>G[N]; int col[N], a[N], tot, dp[2020 ][110 ];typedef pair<int , int >pii;priority_queue<pii, vector<pii>, greater<pii> >q; void dij (int * d) while (!q.empty ()) { int u = q.top ().second, di = q.top ().first; q.pop (); if (di > d[u])continue ; for (E& e : G[u]) { int v = e.v, w = e.w; if (d[v] > d[u] + w) { d[v] = d[u] + w; q.push ({ d[v],v }); } } } } vector<int >vc[110 ]; int main () scanf ("%d%d%d%d%d" , &n, &m, &k, &x, &y); tot = k; for (int i = 1 ; i <= n; i++) { scanf ("%d" , &a[i]); if (a[i])vc[a[i]].push_back (i); } a[x] = ++k; a[y] = ++k; for (int i = 1 ; i <= m; i++) { int u, v, w; scanf ("%d%d%d" , &u, &v, &w); if (a[u] == a[v] && a[u])continue ; G[u].push_back ({ v,w }); G[v].push_back ({ u,w }); } for (int i = 1 ; i <= k; i++) { for (int j = 0 ; j < (int )vc[i].size (); j++) { for (int k = j + 1 ; k < (int )vc[i].size (); k++) { G[vc[i][j]].push_back ({ vc[i][k],0 }); G[vc[i][k]].push_back ({ vc[i][j],0 }); } } } memset (dp, 0x3f , sizeof for (int i = 1 ; i <= n; i++) { if (a[i] != 0 ) { dp[1 << (a[i] - 1 )][i] = 0 ; } } for (int s = 0 ; s < (1 << k); s++) { for (int i = 1 ; i <= n; i++) { for (int t = (s - 1 )&s; t; t = (t - 1 )&s) { dp[s][i] = min (dp[s][i], dp[t][i] + dp[s^t][i]); } if (dp[s][i] != INF)q.push ({ dp[s][i],i }); } dij (dp[s]); } printf ("%d\n" , dp[(1 << k) - 1 ][x]); return 0 ; }