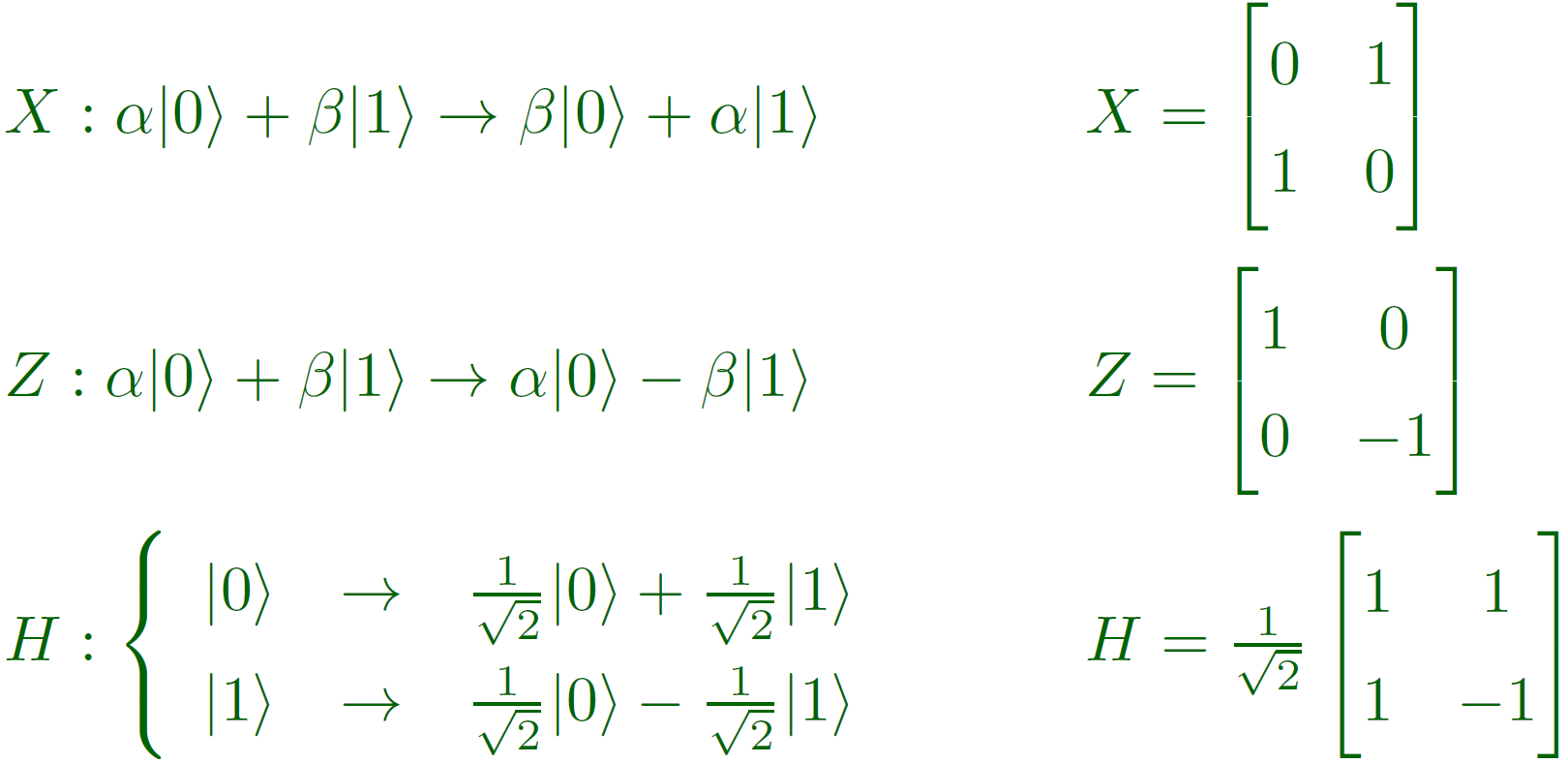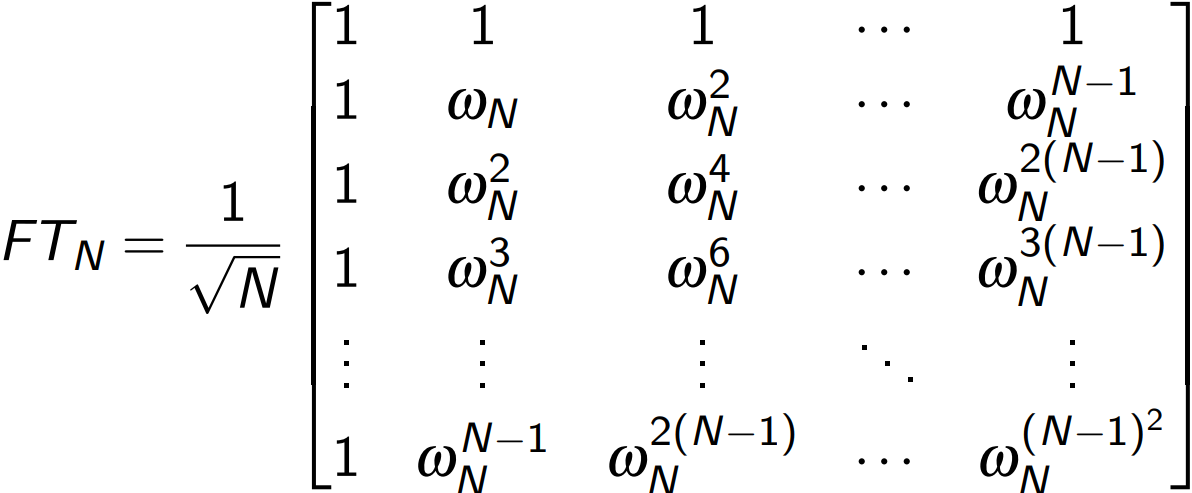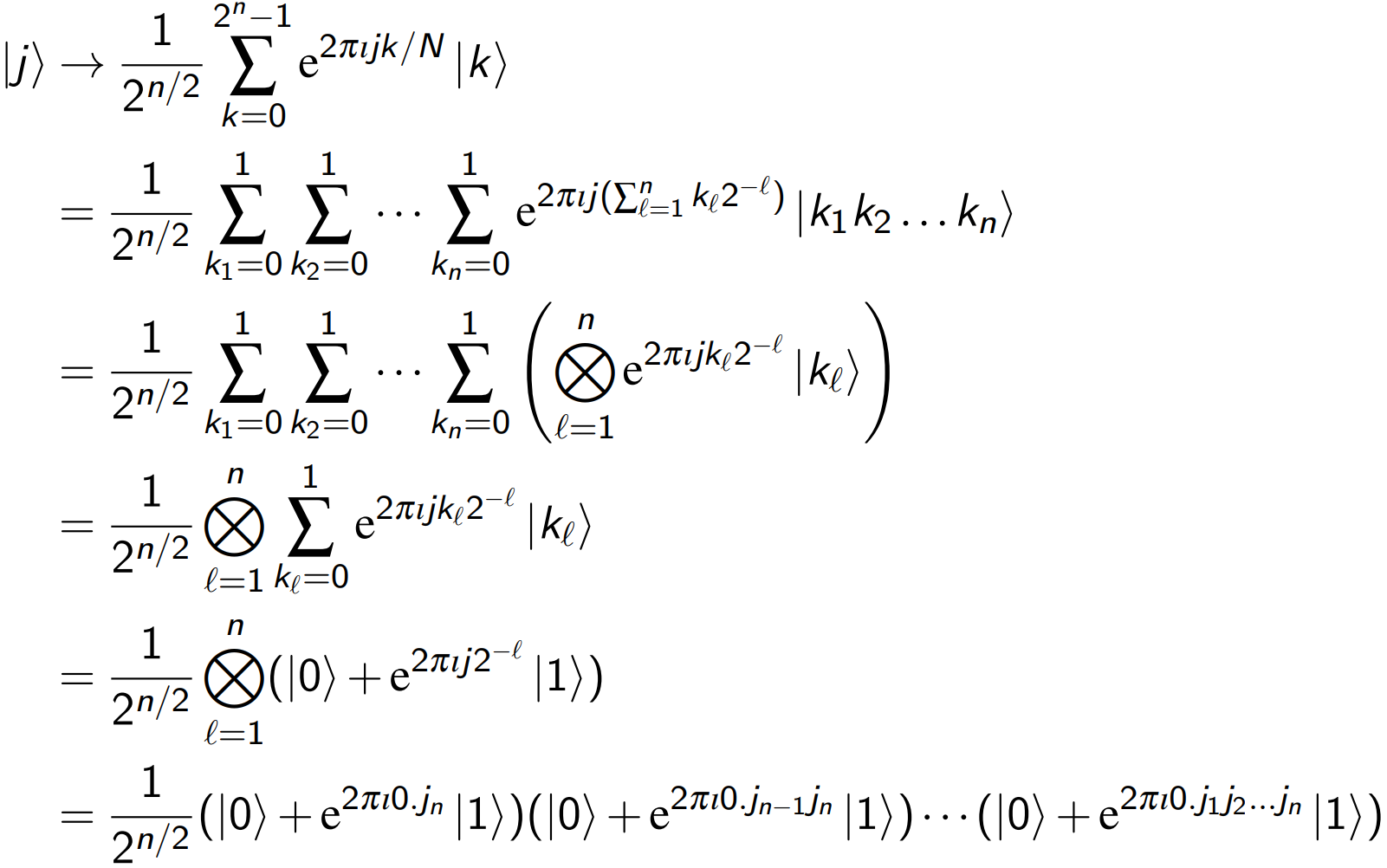表示

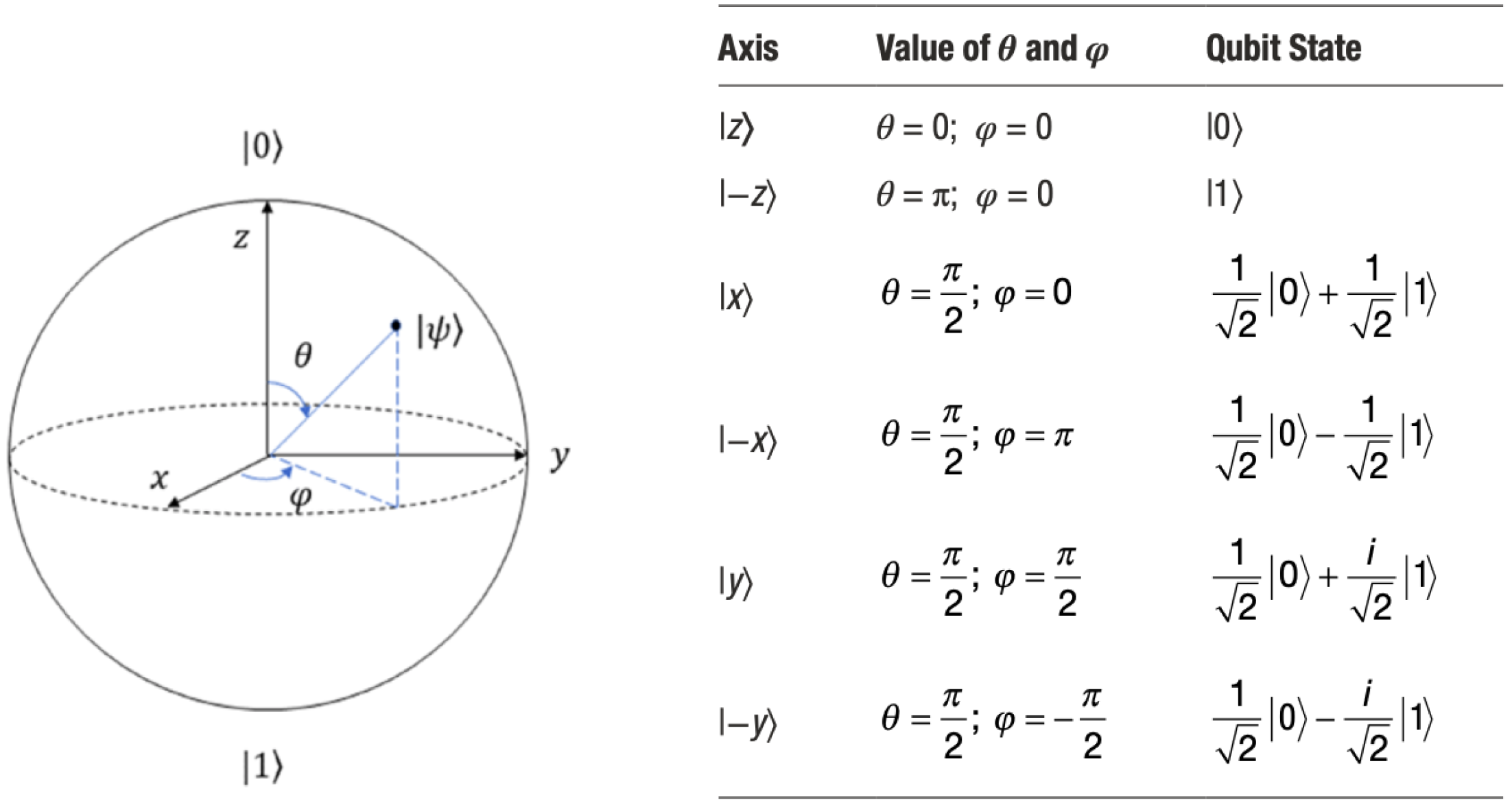
image-20230101123321738

布洛赫球表面的任何一点表示一个量子比特的状态，换句话说，任何一个量子比特的状态 ∣ψ⟩\ket{\psi} 都可以用三个参数 γ,θ,φ\gamma,\theta,\varphi 来表示：

∣ψ⟩=eiγ(cos⁡θ2∣0⟩+sin⁡θ2eiφ∣1⟩)\ket{\psi}=e^{i\gamma}(\cos\frac{\theta}{2}\ket{0}+\sin\frac{\theta}{2}e^{i\varphi}\ket{1})

其中全局相位因子 eiγe^{i\gamma} 在实验中是不可观测的。

运算

基础

转置：∣ψ⟩,⟨ψ∣\ket{\psi},\bra{\psi} 共轭转置。

内积：⟨ψ1∣ψ2⟩\braket{\psi_1|\psi_2} 得到复数值。

∥∣ψ⟩∥=⟨ψ∣ψ⟩\|\ket{\psi}\|=\sqrt{\braket{\psi|\psi}}，如果 ∣ψ⟩\ket{\psi} 是一个量子态，那么一定有 ⟨ψ∣ψ⟩=1\braket{\psi|\psi}=1.

外积：∣ψ1⟩⟨ψ2∣\ket{\psi_1}\bra{\psi_2} 得到 m×nm\times n 的矩阵。

张量积：∣ψ1⟩⊗∣ψ2⟩\ket{\psi_1}\otimes \ket{\psi_2} 得到 Cm×n\mathbb{C}^{m\times n} 中的向量，相当于空间维度扩大，常缩写为 ∣ψ1ψ2⟩\ket{\psi_1\psi_2}.

∣ψ1⟩⊗∣ψ2⟩=∣ψ1ψ2⟩=[c1c2]⊗[d1d2d3]=[c1d1c1d2c1d3c2d1c2d2c2d3]\ket{\psi_1}\otimes\ket{\psi_2}=\ket{\psi_1\psi_2}=\begin{bmatrix}c_1\\c_2\end{bmatrix}\otimes \begin{bmatrix}d_1\\d_2\\d_3\end{bmatrix}=\begin{bmatrix}c_1d_1\\c_1d_2\\c_1d_3\\c_2d_1\\c_2d_2\\c_2d_3\end{bmatrix}

张量积满足分配律：

∣ψ1⟩⊗∣ψ2⟩=(α1∣0⟩+β1∣1⟩)⊗(α2∣0⟩+β2∣1⟩)=α1α2∣00⟩+α1β2∣01⟩+β1α2∣10⟩+β1β2∣11⟩\begin{align} \ket{\psi_1}\otimes\ket{\psi_2}&=(\alpha_1\ket{0}+\beta_1\ket{1})\otimes(\alpha_2\ket{0}+\beta_2\ket{1})\\ &=\alpha_1\alpha_2\ket{00}+\alpha_1\beta_2\ket{01}+\beta_1\alpha_2\ket{10}+\beta_1\beta_2\ket{11} \end{align}

  • A⊗B=[a11B⋯a1nB⋮⋮am1B⋯amnB]A\otimes B=\begin{bmatrix}a_{11}B&\cdots&a_{1n}B\\\vdots & &\vdots\\a_{m1}B&\cdots&a_{mn}B\end{bmatrix}
  • (A⊗B)∗=A∗⊗B∗(A\otimes B)^*=A^*\otimes B^*
  • (A⊗B)⊤=A⊤⊗B⊤(A\otimes B)^\top=A^\top\otimes B^\top
  • (A⊗B)†=A†⊗B†(A\otimes B)^\dagger=A^\dagger\otimes B^\dagger
  • (A⊗B)(C⊗D)=AC⊗BD(A\otimes B)(C\otimes D)=AC\otimes BD

迹： 矩阵对角线上元素之和。

  • tr(AB)=tr(BA)tr(AB)=tr(BA)
  • tr(A+B)=tr(A)+tr(B)tr(A+B)=tr(A)+tr(B)
  • 对任何线性算子 AA 和标量 c∈Cc\in\mathbb{C}，有 tr(cA)=c×tr(A)tr(cA)=c\times tr(A).
  • 对任何酉算子 UU，有 tr(UAU†)=tr(A)tr(UAU^\dagger)=tr(A).
  • 令 {∣ψi⟩}\{\ket{\psi_i}\} 是希尔伯特空间 H\mathcal{H} 上的一组标准正交基，A∈L(H)A\in \mathcal{L}(\mathcal{H}) 是 H\mathcal{H} 上的一个线性算子，有 tr(A)=∑i⟨ψi∣A∣ψi⟩tr(A)=\sum\limits_i\bra{\psi_i}A\ket{\psi_i}.
  • 对任何密度算子 ρ\rho，有 tr(ρ)=1tr(\rho)=1。如果 ρ\rho 是一个纯态，那么 tr(ρ2)=1tr(\rho^2)=1；如果 ρ\rho 是一个混合态，那么 tr(ρ2)<1tr(\rho^2)<1.

单量子比特门

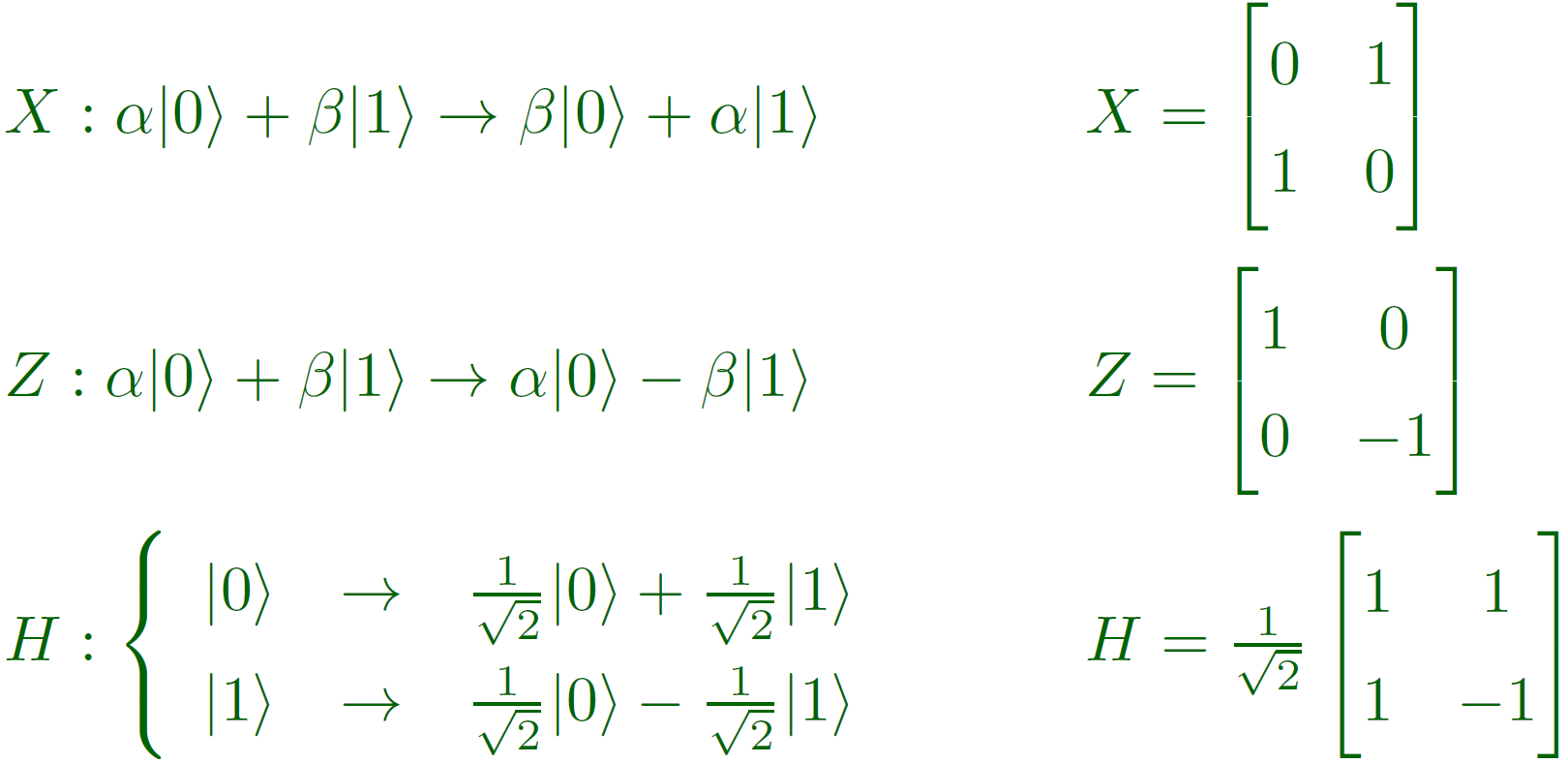
image-20230101124123987

多量子比特门

CNOT门：CNOT:∣A,B⟩→∣A,B⊕A⟩CNOT:\ket{A,B}\to\ket{A,B\oplus A}.

Toffoli门：Toffoli:∣A,B,C⟩→∣A,B,C⊕A⋅B⟩Toffoli:\ket{A,B,C}\to\ket{A,B,C\oplus A\cdot B}.

算法

量子隐形传态

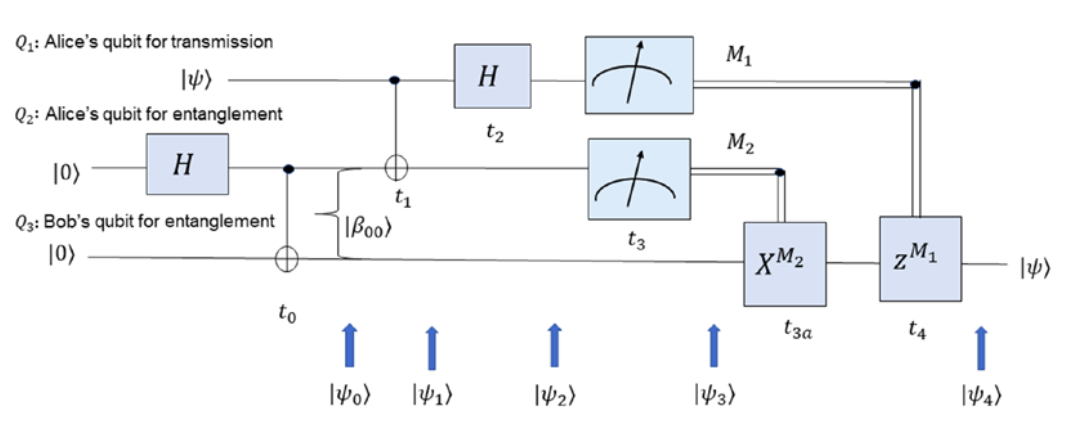
image-20230101124246580

问题：利用仅能传输经典比特的信道传输量子比特Q1Q_1。

过程：Alice和Bob先共同制备贝尔态 ∣Q2Q3⟩\ket{Q_2Q_3}。分开后，Alice通过对她的量子比特Q2Q_2以及想要传输的量子比特Q1Q_1做一系列操作后测量，将测量结果M1,M2M_1,M_2通过经典比特传输信道告知Bob，Bob根据M1,M2M_1,M_2对Q3Q_3施加相应门，使Q3Q_3变为Q1Q_1。

量子并行

量子并行

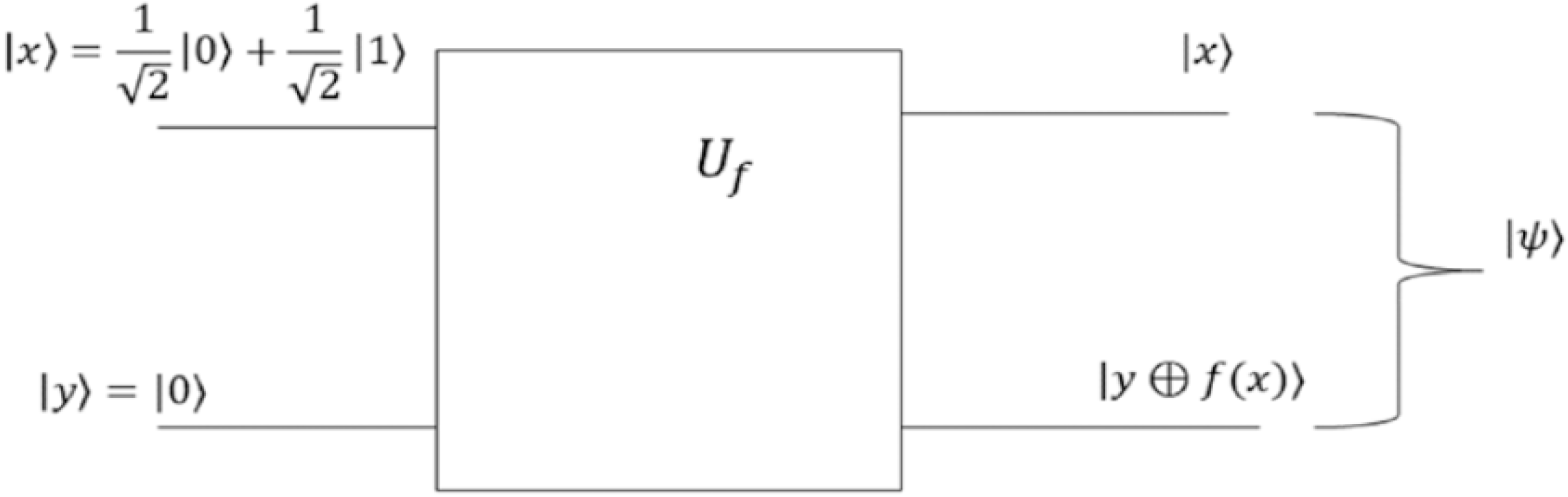
问题：对于函数 f:{0,1,2,⋯ ,2n−1}→{0,1}f:\{0,1,2,\cdots,2^{n}-1\}\to\{0,1\}，得到所有可能的 (x,f(x))(x,f(x)) 二元组的均匀叠加。

过程：先对 ∣00..0⟩\ket{00..0} 的每个比特施加H门，得到 {∣0⟩,∣1⟩,∣2⟩,⋯ ,∣2n−1⟩}\{\ket 0,\ket 1,\ket 2,\cdots,\ket{2^n-1}\} 的均匀叠加，再经过 UfU_f门。

Deutsch算法

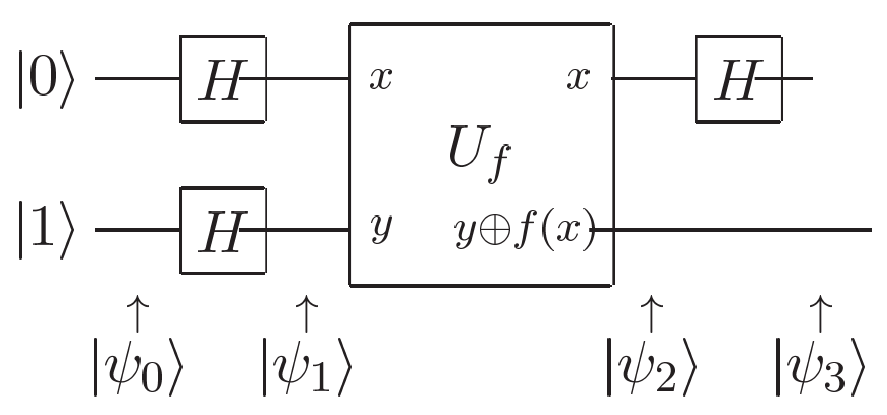
Deutsch算法

问题：用一次对 ff 的求值操作判断 f:{0,1}→{0,1}f:\{0,1\}\to\{0,1\} 是否为一个常函数。

过程：测量 ∣ψ3⟩\ket{\psi_3} 的第一个量子比特的结果就是 f(0)⊕f(1)f(0)\oplus f(1).

Deutsch-Jozsa算法

Deutsch-Jozsa算法

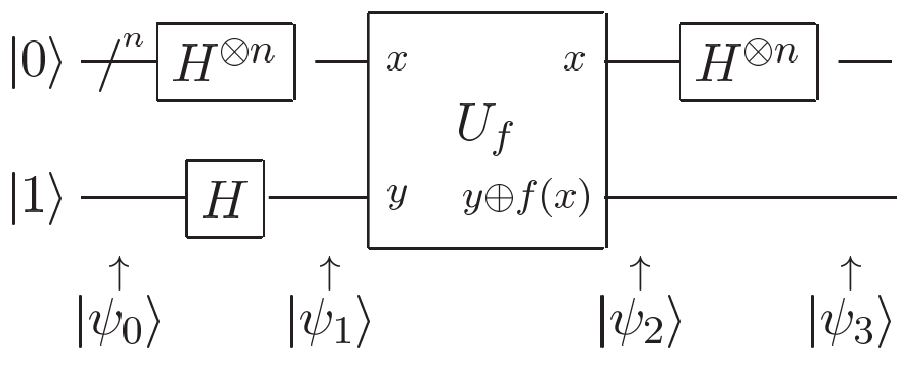
问题：用一次对 ff 的求值操作判断 f:{0,1}n→{0,1}f:\{0,1\}^n\to\{0,1\} 是常函数还是平衡函数（对一半的输入，输出 11）。

过程：测量 ∣ψ3⟩\ket{\psi_3} 的前 nn 个量子比特，如果全为 00，则 ff 是常函数，否则是平衡函数。

Bernstein-Vazirani算法

电路图同Deutsch-Jozsa算法。

Bernstein-Vazirani算法

问题：有 fs:{0,1}n→{0,1},fs(x)=s⋅x(mod  2)f_s:\{0,1\}^n\to\{0,1\},f_s(x)=s\cdot x(\mod 2)，用一次对 fsf_s 的求值操作求出 s∈{0,1}ns\in\{0,1\}^n.

过程：测量 ∣ψ3⟩\ket{\psi_3} 的前 nn 个量子比特，结果就是 ss.

Simon算法

Simon算法

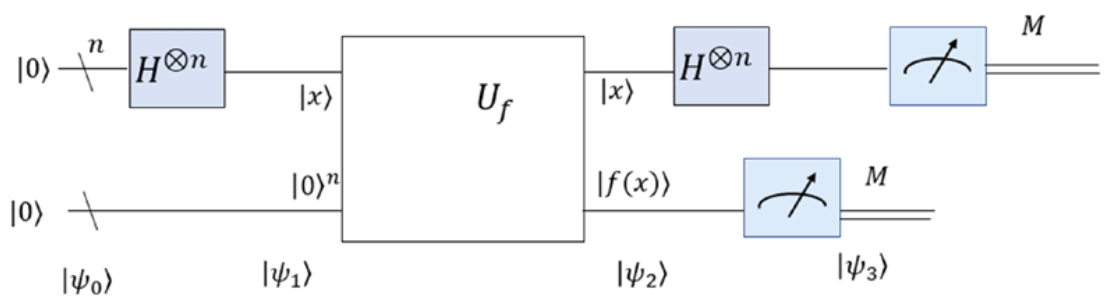
问题：有 f:{0,1}n→{0,1}nf:\{0,1\}^n\to\{0,1\}^n 一定是双射的(one-to-one)或者二对一(two-to-one)的函数，且若 ff 是二对一的函数，必定存在 ss 使得：f(x1)=f(x2)f(x_1)=f(x_2) 当且仅当 x1⊕x2=sx_1\oplus x_2=s，求出 s∈{0,1}ns\in\{0,1\}^n.

过程：多次测量 ∣ψ3⟩\ket{\psi_3} 的前 nn 个量子比特，直至观测到 nn 个不同的 z∈{0,1}nz\in\{0,1\}^n，分别记为 z1,z2,⋯ ,znz_1,z_2,\cdots,z_n，则得到以下方程组：

s⋅z1=0s⋅z2=0⋮s⋅zn=0s\cdot z_1=0\\ s\cdot z_2=0\\ \vdots\\ s\cdot z_n=0\\

高斯消元法求解方程组，结果就是 ss.

量子超密编码

量子超密编码

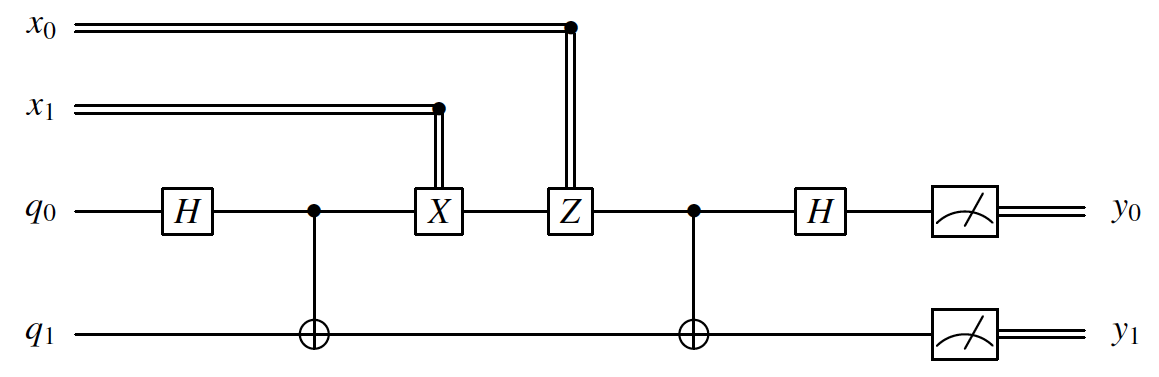
问题：利用一对贝尔态 q0,q1q_0,q_1 和仅能传输量子比特的信道传输两个经典比特 x0,x1x_0,x_1.

过程：Alice和Bob先共同制备贝尔态 ∣q0q1⟩\ket{q_0q_1}。分开后，Alice根据 x0,x1x_0,x_1 的值，向 q0q_0 施加X门以及Z门。Alice把 q0q_0 传输给Bob，Bob向 q0q1q_0q_1 作用CNOT门，再向 q0q_0 作用H门。最后，Bob测量 q0q1q_0q_1，结果即为 x0x1x_0x_1.

数学

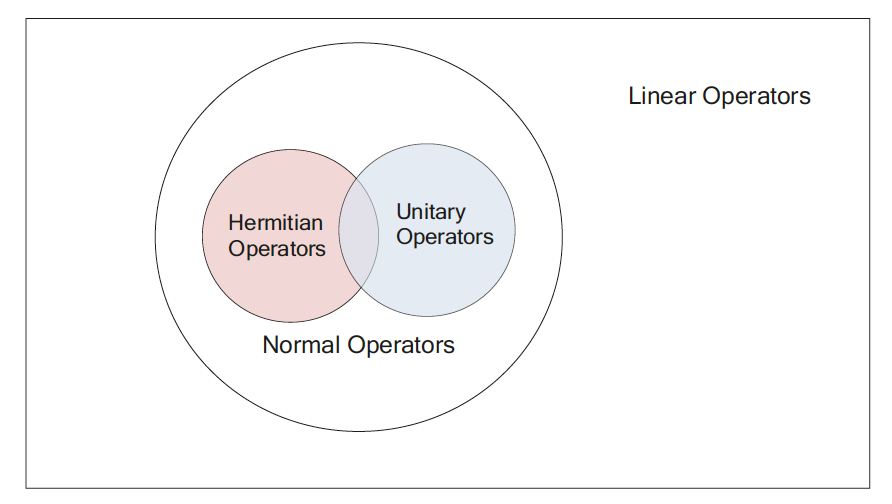
image-20230101222454242

线性算子

定义： 令 H,K\mathcal{H},\mathcal{K} 为两个希尔伯特空间（每个柯西序列都有极限的完备的内积空间），如果一个映射 A:H→KA:\mathcal{H}\to\mathcal{K} 满足下面两个条件，则称 AA 是一个线性算子。

  1. A(∣u⟩+∣v⟩)=A∣u⟩+A∣v⟩A(\ket{u}+\ket{v})=A\ket{u}+A\ket{v}
  2. A(c∣v⟩)=cA∣v⟩A(c\ket{v})=cA\ket{v}

线性算子上的运算：

  • (A+B)∣v⟩=A∣v⟩+B∣v⟩(A+B)\ket{v}=A\ket{v}+B\ket{v}
  • (cA)∣v⟩=c(A∣v⟩)(cA)\ket{v}=c(A\ket{v})
  • (BA)∣v⟩=B(A∣v⟩)(BA)\ket{v}=B(A\ket{v})

矩阵表示： 通常，线性算子存在矩阵表示。令H,K\mathcal{H},\mathcal{K} 分别是 nn 维，mm 的希尔伯特空间，基分别为 {∣v1⟩,⋯ ,∣vn⟩},{∣w1⟩,⋯ ,∣wm⟩}\{\ket{v_1},\cdots, \ket{v_n}\},\{\ket{w_1},\cdots, \ket{w_m}\}，A:H→KA:\mathcal{H}\to\mathcal{K} 是一个线性算子，AA 的矩阵记为表示 MAM_A. 则当 {∣v1⟩,⋯ ,∣vn⟩},{∣w1⟩,⋯ ,∣wm⟩}\{\ket{v_1},\cdots, \ket{v_n}\},\{\ket{w_1},\cdots, \ket{w_m}\} 都是标准正交基时，MAM_A 的第 ii 行第 jj 列的元素 Aij=⟨wi∣A∣vj⟩A_{ij}=\bra{w_i}A\ket{v_j}.

对角化表示： 如果线性算子 AA 的特征向量 ∣k⟩\ket{k} 是标准正交的，分别对应特征值 λk\lambda_k，那么有 A=∑kλk∣k⟩⟨k∣A=\sum\limits_k\lambda_k\ket{k}\bra{k}.

伴随： 对任何线性算子 A∈L(H)A\in \mathcal L(\mathcal H)，存在唯一的算子 A†A^\dagger 满足：(A∣u⟩,∣v⟩)=(∣u⟩,A†∣v⟩)(A\ket{u},\ket{v})=(\ket{u},A^\dagger\ket{v}).

A†A^\dagger 的矩阵表示等于 AA 的矩阵表示的共轭转置。

对任何线性算子 A,BA,B，有 (AB)†=B†A†(AB)^\dagger=B^\dagger A^\dagger 且 (A†)†=A(A^\dagger)^\dagger=A.

正规算子

定义： 如果一个线性算子 AA 与其伴随 A†A^\dagger 对易，即 AA†=A†AAA^\dagger=A^\dagger A，则称 AA 是一个正规算子。

性质：

  1. 正规算子可以进行谱分解：A=∑kλk∣k⟩⟨k∣A=\sum\limits_k\lambda_k\ket{k}\bra{k}.
  2. 正规算子 AA 上的函数 ff 可以被定义为 f(A)=∑if(λi)∣i⟩⟨i∣f(A)=\sum\limits_if(\lambda_i)\ket{i}\bra{i}.

厄米算子

定义： 如果一个正规算子 MM 是自伴随的，即 M†=MM^\dagger=M，则称 MM 是一个厄米算子。

性质：

  1. 厄米算子的所有特征值都是实数。
  2. 空间 H\mathcal{H} 上一个算子 MM 是厄米的当且仅当对所有 ∣v⟩∈H\ket{v}\in \mathcal{H}，数值 ⟨v∣M∣v⟩\bra{v}M\ket{v} 是实数。

投影算子

定义： 一组正交基 ∣1⟩,∣2⟩,⋯ ,∣m⟩\ket{1},\ket{2},\cdots,\ket{m}，则 P=∑i=1m∣i⟩⟨i∣P=\sum\limits_{i=1}^m\ket{i}\bra{i} 是一个投影算子。

性质：

  • 一个投影算子一定是一个厄密算子。
  • 对一个厄密算子 MM 进行谱分解 M=∑λ∈spec(M)λPλM=\sum\limits_{\lambda\in spec(M)}\lambda P_\lambda. 则得到的 Pλ=∣λ⟩⟨λ∣P_\lambda=\ket{\lambda}\bra{\lambda} 是一个投影算子，从 H\mathcal{H} 投影到 λ\lambda 对应的特征空间。

酉算子

定义： 如果一个正规算子 UU 满足 U†U=UU†=IU^\dagger U=UU^\dagger=I，则称 UU 是一个酉算子。

性质：

  1. 所有酉算子保持内积，即 (U∣u⟩,U∣v⟩)=⟨u∣v⟩(U\ket{u},U\ket{v})=\braket{u|v}.
  2. tr(UAU†)=tr(A)tr(UAU^\dagger)=tr(A)

量子力学基本假设

量子状态

一个封闭量子系统的状态空间可以由一个希尔伯特空间表示，这个系统的纯态可由状态空间上的一个单位向量表示。

量子演化

一个封闭系统的演化可以由一个酉变换来描述。如果这个系统在 t0t_0 和 t1t_1 时刻的状态为 ∣ψ0⟩\ket{\psi_0} 和 ∣ψ1⟩\ket{\psi_1}，那么存在一个酉算子 UU 使得 ∣ψ1⟩=U∣ψ0⟩\ket{\psi_1}=U\ket{\psi_0}.

量子测量

一般测量：

对一个状态空间为 H\mathcal{H} 的系统进行的一般测量可以由一组测量算子 {Mm}⊆L(H)\{M_m\}\subseteq \mathcal{L}(\mathcal{H}) 描述。

要求： 这组测量算子满足完备性等式：∑mMm†Mm=IH\sum_mM_m^\dagger M_m=I_{\mathcal{H}}，其中下标 mm 代表实验中可能出现的测量结果。

若测量前的系统状态为 ∣ψ⟩\ket \psi，那么对于每个 mm，

  • 测量结果 mm 出现的概率为 p(m)=∥Mm∣ψ⟩∥2=⟨ψ∣M†M∣ψ⟩p(m)=\|M_m\ket{\psi}\|^2=\bra{\psi} M^\dagger M\ket{\psi}.
  • 测量结果 mm 出现后系统状态变为 ∣ψm⟩=Mm∣ψ⟩p(m)\ket{\psi_m}=\frac{M_m\ket{\psi}}{\sqrt{p(m)}}.

投影测量：

是一般测量的一种特殊情况。

要求： 除了要求测量算子满足完备性等式外，还要求它是一个投影算子，即满足 Pm†Pm=Pm2=PmP_m^\dagger P_m=P_m^2=P_m，它把 ∣ψ⟩\ket{\psi} 投影到希尔伯特空间上的一组完备基 {∣ψm⟩}\{\ket{\psi_m}\} 上，其中 Pm=∣ψm⟩⟨ψm∣P_m=\ket{\psi_m}\bra{\psi_m}.

若测量前的系统状态为 ∣ψ⟩\ket \psi，那么对于每个 mm，

  • 测量结果 mm 出现的概率为 p(m)=⟨ψ∣Pm∣ψ⟩p(m)=\bra{\psi} P_m\ket{\psi}.
  • 测量结果 mm 出现后系统状态变为 Pm∣ψ⟩p(m)\frac{P_m\ket{\psi}}{\sqrt{p(m)}}.

任何一个可观测的量 MM 都是一个厄密算子，它定义了一个测量 {Pm∣m∈spec(M)}\{P_m|m\in spec(M)\}，这个测量必定是投影测量。观测量 MM 对状态 ∣ψ⟩\ket{\psi} 的测量结果期望值为：⟨M⟩ψ=⟨ψ∣M∣ψ⟩\braket{M}_{\psi}=\bra{\psi}M\ket{\psi}.

海森堡不确定性原理： 令 M,NM,N 是两个可观测的量，它们在状态 ∣ψ⟩\ket{\psi} 上的标准差满足 ΔMΔN≥12∥∣ψ⟩[M,N]⟨ψ∣∥\Delta M\Delta N\ge \frac{1}{2}\|\ket{\psi}[M,N]\bra{\psi}\|，即无法使两个可观测量都有低标准差。

复合系统

一个复合系统的状态空间是各子系统状态空间的张量积。否则这个复合系统的状态是纠缠的。纠缠的系统不能描述为 ∣q0q1⟩\ket{q_0q_1} 的形式。

密度算子

定义： 对于混合态，可以用纯态的系综 {(∣ψ⟩,pi)}\{(\ket{\psi},p_i)\} 来表示。也可以用密度算子 ρ=∑ipi∣ψi⟩⟨ψi∣\rho=\sum\limits_ip_i\ket{\psi_i}\bra{\psi_i} 来表示。

性质：

  • 对任何密度算子 ρ\rho，ρ\rho 是正算子且 tr(ρ)=1tr(\rho)=1.
  • 一个系综对应一个密度算子，但一个密度算子可以对应多个系综。
  • 如果 ρ\rho 是一个纯态，那么 tr(ρ2)=1tr(\rho^2)=1；如果 ρ\rho 是一个混合态，那么 tr(ρ2)<1tr(\rho^2)<1.

约简密度算子

定义： 用于刻画一个复合系统的子系统的密度算子。令 S,TS,T 是两个量子系统，分别处于希尔伯特空间 HS,HT\mathcal{H}_S,\mathcal{H}_T. 令 ρ\rho 是复合系统 HS⊗HT\mathcal{H}_S\otimes\mathcal{H}_T 的密度算子。它在系统 SS 上的约简密度算子为 ρS=trT(ρ)\rho_S=tr_T(\rho)，其中 trT(ρ)tr_T(\rho) 表示在系统 TT 上的偏迹操作：trT(∣ψ⟩⟨ϕ∣⊗∣θ⟩⟨ξ∣)=⟨ξ∣θ⟩⋅∣ψ⟩⟨ϕ∣tr_T(\ket{\psi}\bra{\phi}\otimes\ket{\theta}\bra{\xi})=\braket{\xi|\theta}\cdot \ket{\psi}\bra{\phi}.

Grover算法

问题： 在一个无结构的数据库中（即没有红黑树之类），从 NN 条记录中找出一条指定的记录，时间复杂度 O(N)\mathcal{O}(\sqrt{N}).

量子电路： Grover算法需要 nn 个量子位来对应 N=2nN=2^n 条记录的编号，以及一些额外的工作位以完成神谕机（oracle）受控的操作。

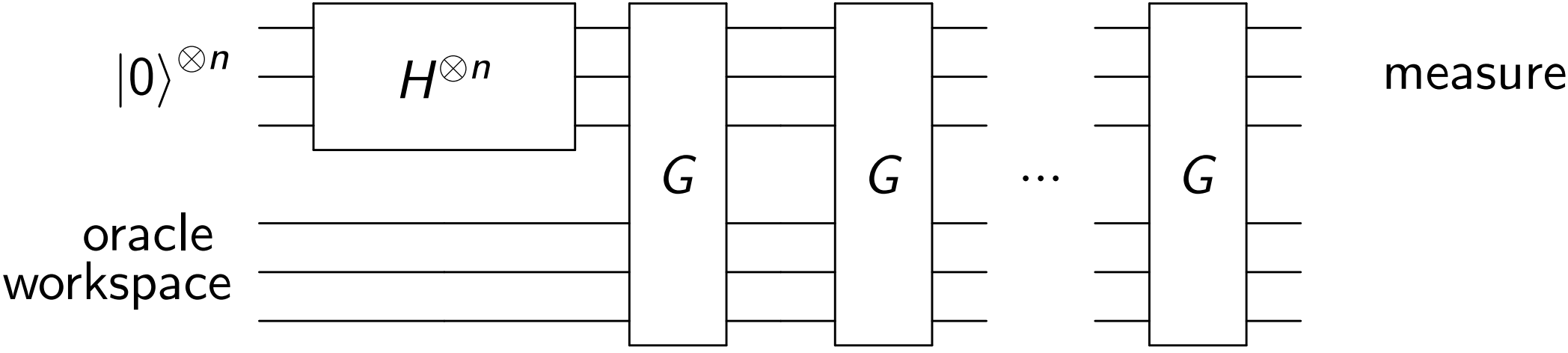
image-20230102183521193

过程： 首先对 nn 个量子位做 HH 门，使各记录都有相同的概率 1N\frac{1}{N} 被选中，再通过多次Grover迭代（G门）以逐步增大目标记录被选中的概率，最后测量。

Grover迭代（G门）：

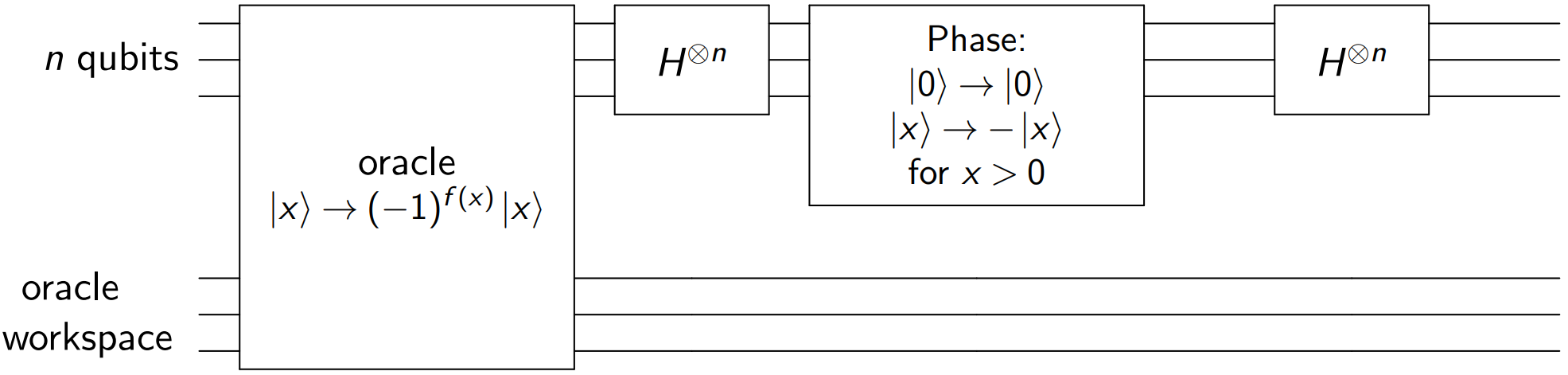
image-20230102184155201
  1. 作用神谕机受控操作 OO，使得目标记录乘以相位 −1-1.
  2. 作用H门 H⊗nH^{\otimes n}.
  3. 执行条件相位变换，使得除了 ∣0⟩\ket{0} 以外的每个计算基态乘以相位 −1-1，即 ∣x⟩→−∣x⟩ if x≠0⊗n\ket{x}\to -\ket{x}\ \text{if } x\neq 0^{\otimes n}. 对应酉算子 2∣0⟩⟨0∣−I2\ket{0}\bra{0}-I.
  4. 再作用H门 H⊗nH^{\otimes n}.

步骤2-4对应酉算子 H⊗n(2∣0⟩⟨0∣−I)H⊗n=2H⊗n∣0⟩⟨0∣H⊗n−H⊗nIH⊗n=2∣ϕ⟩⟨ϕ∣−IH^{\otimes n}(2\ket{0}\bra{0}-I)H^{\otimes n}=2H^{\otimes n}\ket{0}\bra{0}H^{\otimes n}-H^{\otimes n}IH^{\otimes n}=2\ket{\phi}\bra{\phi}-I，其中 ∣ϕ⟩=1N∑x=0N−1∣x⟩\ket{\phi}=\frac{1}{\sqrt{N}}\sum_{x=0}^{N-1}\ket{x}.

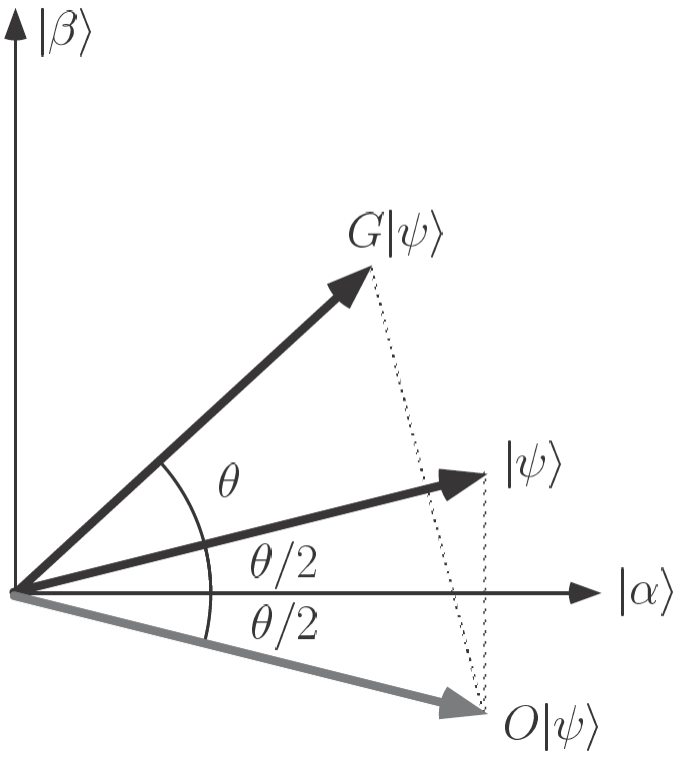
Grover迭代对应酉算子 (2∣ϕ⟩⟨ϕ∣−I)O(2\ket{\phi}\bra{\phi}-I)O.

随着Grover迭代，搜索成功的概率：sin⁡2(θ2)→sin⁡2(3θ2)→sin⁡2(5θ2)→⋯\sin^2(\frac{\theta}{2})\to\sin^2(\frac{3\theta}{2})\to\sin^2(\frac{5\theta}{2})\to\cdots.

image-20230102224036501

Shor算法

量子傅里叶变换

傅里叶变换

定义： 一个复数向量之间的映射 (x0,…,xN−1)→(y0,…,yN−1)(x_0,\dots,x_{N-1})\to (y_0,\dots,y_{N-1})，具体为 yk=1N∑j=0N−1xje2πijk/Ny_k=\frac{1}{\sqrt{N}}\sum\limits_{j=0}^{N-1}x_je^{2\pi ijk/N}，其中 k=(0,1,…,N−1)k=(0,1,\dots,N-1).

FT是一个酉变换，令 ωN=e2πi/N\omega_N=e^{2\pi i/N} 是 xN=1x^N=1 的单位根，则

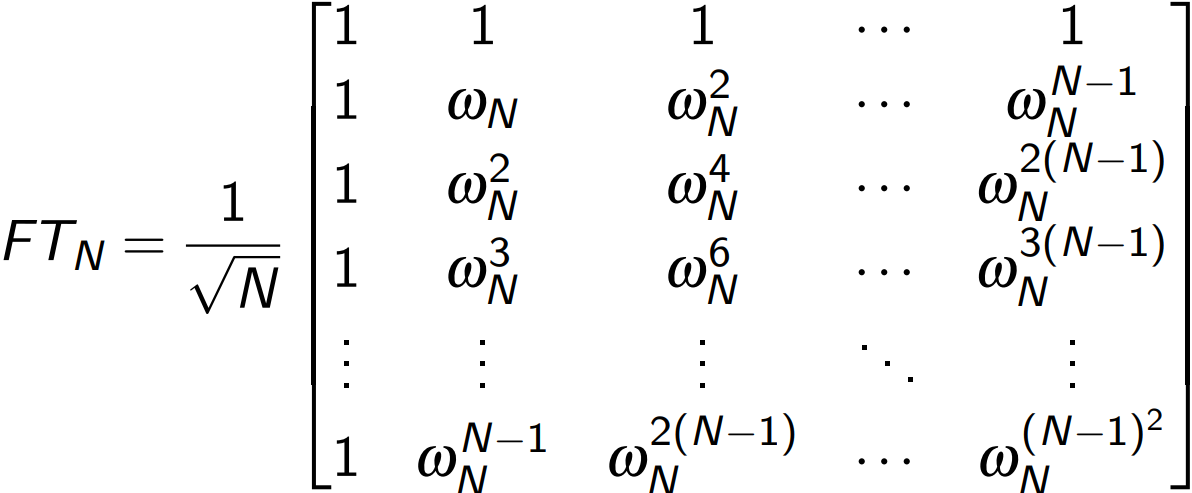
image-20230102234437984

快速傅里叶变换

yk=12(ykmod  N/2even+ωNkykmod  N/2even)y_k=\frac{1}{\sqrt{2}}\left(y^{\text{even}}_{k\mod N/2}+\omega_N^ky^{\text{even}}_{k\mod N/2}\right)

其中 ykmod  N/2even=1N/2∑2∣jωN/2jk/2xjy^{\text{even}}_{k\mod N/2}=\frac{1}{\sqrt{N/2}}\sum_{2|j}\omega_{N/2}^{jk/2}x_j 为 FT(xeven)FT(x^\text{even}) 中下标为 kmod  N/2k\mod N/2 的元素，ykmod  N/2odd=1N/2∑2∤jωN/2(j−1)k/2xjy^{\text{odd}}_{k\mod N/2}=\frac{1}{\sqrt{N/2}}\sum_{2\nmid j}\omega_{N/2}^{(j-1)k/2}x_j 为 FT(xodd)FT(x^\text{odd}) 中下标为 kmod  N/2k\mod N/2 的元素。

时间复杂度 O(Nlog⁡N)\mathcal{O}(N\log N).

量子傅里叶变换

定义：

∣j⟩→1N∑k=0N−1e2πijk/N∣k⟩\ket{j}\to \frac{1}{\sqrt{N}}\sum_{k=0}^{N-1}e^{2\pi ijk/N}\ket{k}

化简：

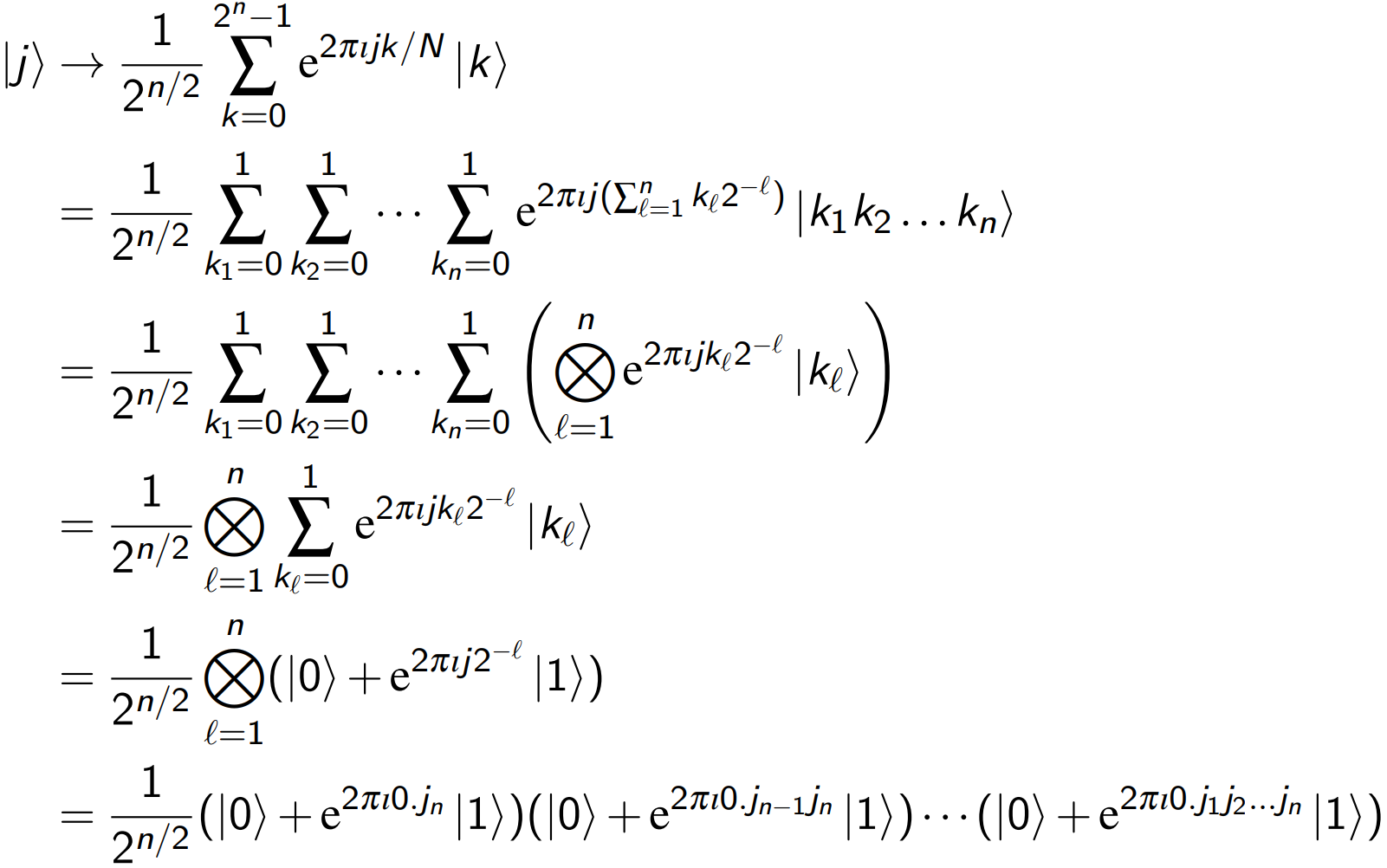
image-20230103112212631

量子电路：

image-20230103111956065

定义旋转门：Rk=[100e2πi/2k]R_k=\begin{bmatrix}1&0\\0&e^{2\pi i/2^k}\end{bmatrix}.

  1. 对输入 ∣jn⟩\ket{j_n} 执行H门，得到第一个因子 [∣0⟩+e2πi0.jn∣1⟩]/2[\ket{0}+e^{2\pi i0.j_n}\ket{1}]/\sqrt{2}.
  2. 对输入 ∣jn−1⟩\ket{j_{n-1}} 执行H门，得到 [∣0⟩+e2πi0.jn−1∣1⟩]/2[\ket{0}+e^{2\pi i0.j_{n-1}}\ket{1}]/\sqrt{2}，再执行由 ∣jn⟩\ket{j_n} 控制的旋转门 R2R_2，得到第二个因子 [∣0⟩+e2πi0.jj−1jn∣1⟩]/2[\ket{0}+e^{2\pi i0.j_{j-1}j_n}\ket{1}]/\sqrt{2}.
  3. 以此类推。
  4. 最后用 ⌊n/2⌋\lfloor n/2\rfloor 个交换门，把序列翻转。

相位估计

相位： 一个酉算子 UU 作用在状态 ∣u⟩\ket{u} 上，假设 ∣u⟩\ket{u} 是 UU 的一个特征态，则有 U∣u⟩=e2πiφ∣u⟩U\ket{u}=e^{2\pi i\varphi}\ket{u}，其中 e2πiφe^{2\pi i\varphi} 是 UU 的特征值，φ\varphi 是 UU 的相位。求出相位后即确定了特征值，就可以通过谱分解确定酉算子 UU.

问题： 有一个黑盒酉算子 UU，假设已有 UU 的各阶完全平方次幂 U20,U21,U22,⋯U^{2^0},U^{2^1},U^{2^2},\cdots 以及特征态 ∣u⟩\ket{u}，求出对应的相位 φ\varphi.

过程：

  • 第一阶段：构造由 Uj∣u⟩U^j\ket{u} 组成的几何级数的叠加态。
  • 第二阶段：用量子傅里叶逆变换还原相位。

第一阶段量子电路：

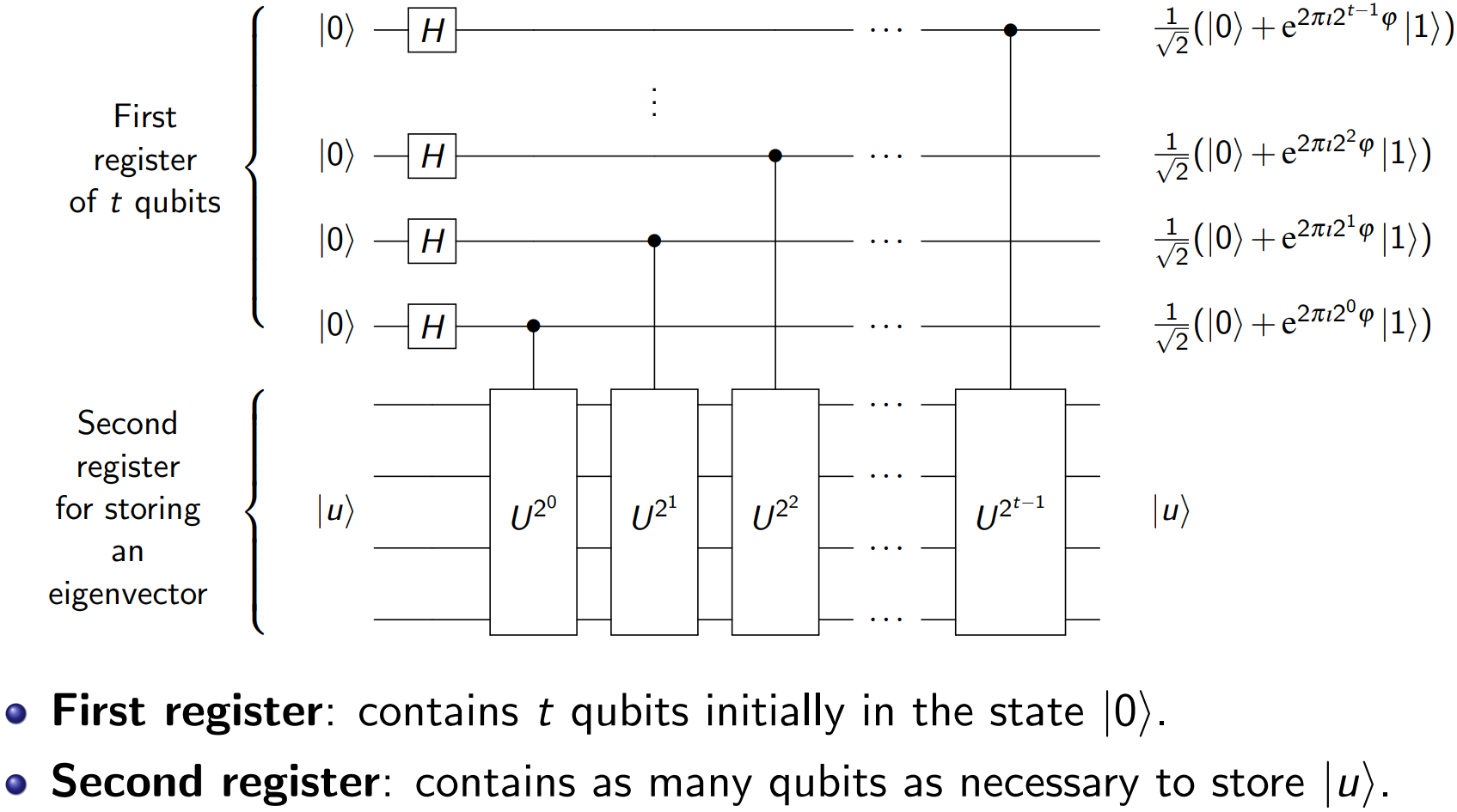
image-20230103123810962

完整量子电路：

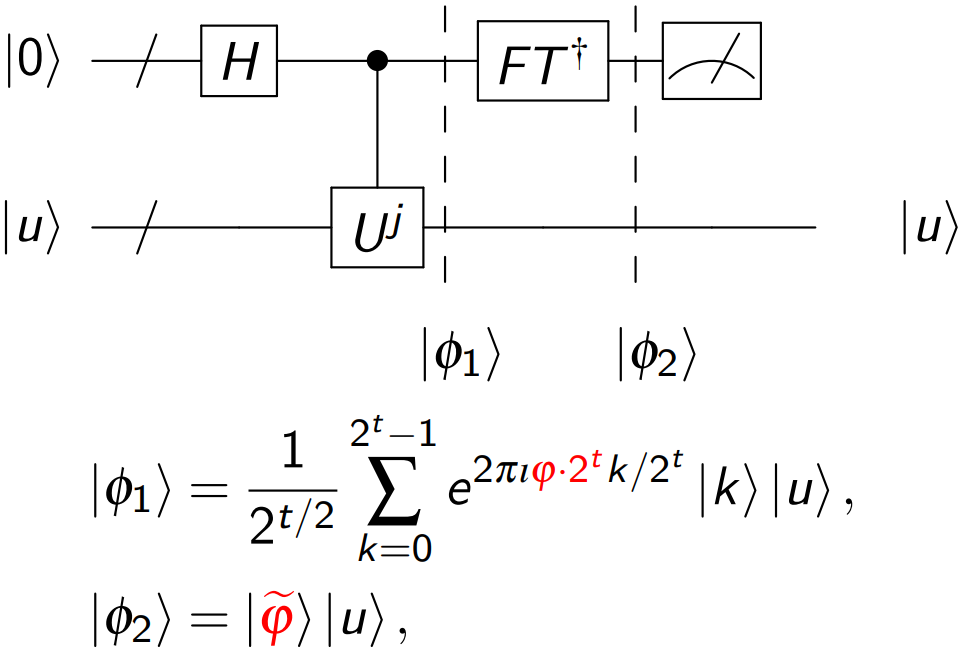
image-20230103123917797

得到 φ~\tilde{\varphi} 是 φ⋅2t\varphi\cdot 2^t 的最佳近似值。

周期计算

问题： 给定两个互素的正整数 x,Nx,N，求满足 xr≡1mod  Nx^r\equiv 1\mod N 的最小正整数 rr.

定义酉算子 U∣y⟩=∣x⋅ymod  N⟩U\ket{y}=\ket{x\cdot y\mod N}.

可证 ∣us⟩≡1N∑k=0r−1exp⁡[−2πiskr]∣xkmod  N⟩\ket{u_s}\equiv \frac{1}{\sqrt{N}}\sum_{k=0}^{r-1}\exp[\frac{-2\pi isk}{r}]\ket{x^k\mod N} 是 UU 的一个特征态，其对应的相位为 s/rs/r，它的分母就是周期 rr.

由于不知道 rr，故无法制备具体的 ss 对应的 ∣us⟩\ket{u_s}，但可以制备所有 ∣us⟩\ket{u_s} 的叠加 1r∑s=0r−1∣us⟩=∣1⟩\frac{1}{\sqrt{r}}\sum_{s=0}^{r-1}\ket{u_s}=\ket{1}.

量子电路：

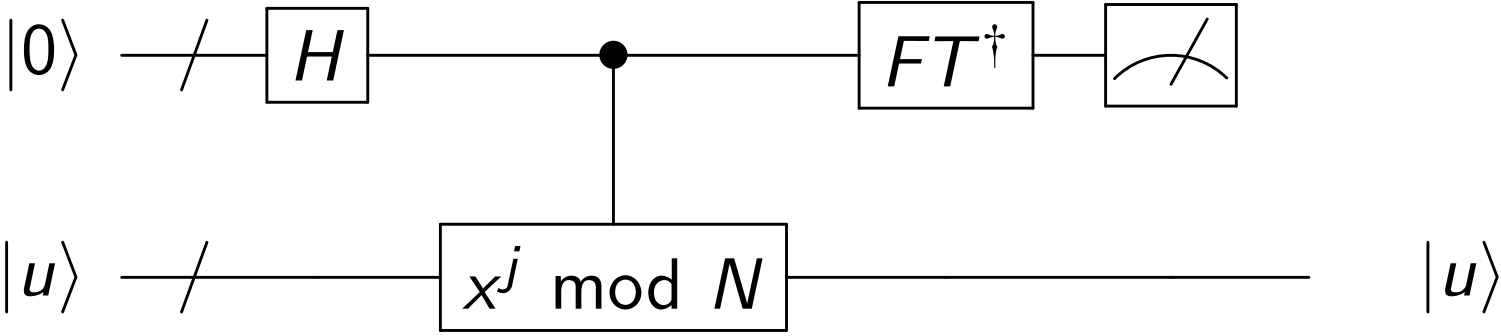
image-20230103170245610
  1. 制备 ∣u⟩=∣1⟩\ket{u}=\ket{1}，即所有特征态的叠加 1r∑s=0r−1∣us⟩=∣1⟩\frac{1}{\sqrt{r}}\sum_{s=0}^{r-1}\ket{u_s}=\ket{1}.
  2. 相位估计得到小数形式的 s/rs/r.
  3. 利用Stern-Brocot树转化为分数形式，得到分母 rr 即为周期。

整数分解

image-20230103170752309