https://vjudge.net/contest/399466#overview

E - Colorful Balloons

 

题意：给定一个数列和 kk，每个数为 11 到 nn，一个区间的权值等于 ∑i=1ncntik\sum_{i=1}^ncnt^k_i，其中 cnticnt_i 为区间中数 ii 的个数，求所有区间的权值之和。

FFT

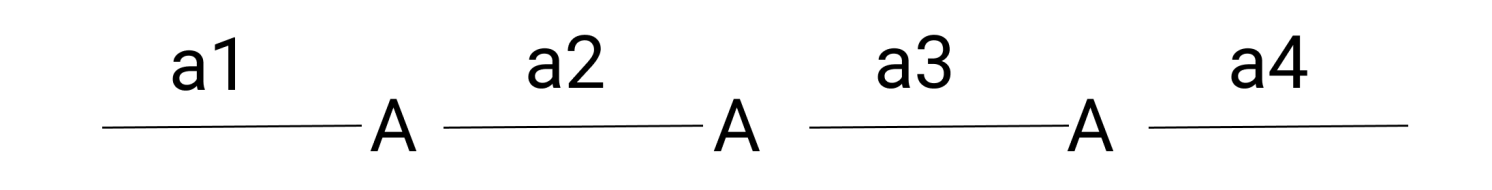
对于数 A，包含一个A的区间数为 a1⋅a2+a2⋅a3+a3⋅a4a1\cdot a2+a2\cdot a3+a3\cdot a4，包含两个A的区间数为 a1⋅a3+a2⋅a4a1\cdot a3+a2\cdot a4，包含三个区间A的区间数为 a1⋅a4a1\cdot a4。

则A的贡献为

(a1∗a2+a2∗a3+a3∗a4)∗1K+(a1∗a3+a2∗a4)∗2K+(a1∗a4)∗3K(a1*a2+a2*a3+a3*a4)*1^K+\\ (a1*a3+a2*a4)*2^K+\\ (a1*a4)*3^K\\

两个多项式

A=a1+a2x+a3x2+a4x3B=a4+a3x+a2x2+a1x3A=a_1+a_2x+a_3x^2+a_4x^3\\ B=a_4+a_3x+a_2x^2+a_1x^3\\

这两个多项式相乘结果为

C=(a1∗a4)+(a1∗a3+a2∗a4)x+(a1∗a2+a2∗a3+a3∗a4)x2+⋯C=(a_1*a_4)+(a_1*a_3+a_2*a_4)x+(a1*a2+a2*a3+a3*a4)x^2+\cdots\\

恰好和上面的贡献对应。

所以可以先求出 a1，a2，a3，a4，再FTT求多项式乘法。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define debug(x) cout << #x << ":\t" << x << endl;
const int N = 2e6 + 10;
const int INF = 0x3f3f3f3f;
const ll inf = 0x3f3f3f3f3f3f3f3f;
const ll mod = 1e9 + 7;
const double PI = acos(-1.0);
struct Complex {
	double x, y;
	Complex(double _x = 0.0, double _y = 0.0) {
		x = _x;
		y = _y;
	}
	Complex operator-(const Complex &b) const {
		return Complex(x - b.x, y - b.y);
	}
	Complex operator+(const Complex &b) const {
		return Complex(x + b.x, y + b.y);
	}
	Complex operator*(const Complex &b) const {
		return Complex(x * b.x - y * b.y, x * b.y + y * b.x);
	}
};
void change(Complex y[], int len) {
	int i, j, k;
	for (i = 1, j = len / 2; i < len - 1; i++) {
		if (i < j) swap(y[i], y[j]);
		k = len / 2;
		while (j >= k) {
			j = j - k;
			k = k / 2;
		}
		if (j < k) j += k;
	}
}
void fft(Complex y[], int len, int on) {
	change(y, len);
	for (int h = 2; h <= len; h <<= 1) {
		Complex wn(cos(2 * PI / h), sin(on * 2 * PI / h));
		for (int j = 0; j < len; j += h) {
			Complex w(1, 0);
			for (int k = j; k < j + h / 2; k++) {
				Complex u = y[k];
				Complex t = w * y[k + h / 2];
				y[k] = u + t;
				y[k + h / 2] = u - t;
				w = w * wn;
			}
		}
	}
	if (on == -1) {
		for (int i = 0; i < len; i++) {
			y[i].x /= len;
		}
	}
}
int n, K;
vector<int>pos[N], vc[N];
Complex a[N], b[N];
ll c[N];
void solve(vector<int>& vc) {
	int n = (int)vc.size();
	int len = 1;
	while (len < 2 * n)len <<= 1;
	for (int i = 0; i <= len; i++) {
		a[i].x = a[i].y = 0;
		b[i].x = b[i].y = 0;
	}
	for (int i = 0; i < n; i++) {
		a[i].x = vc[i];
		b[i].x = vc[n - i - 1];
	}
	fft(a, len, 1);
	fft(b, len, 1);
	for (int i = 0; i < len; i++)a[i] = a[i] * b[i];
	fft(a, len, -1);
	for (int i = 0; i < n - 1; i++) {
		c[n - 1 - i] = (c[n - 1 - i] + (ll)(a[i].x + 0.5)) % mod;
	}
}
ll Pow(ll a, ll b) {
	ll res = 1;
	while (b) {
		if (b & 1)res = res * a%mod;
		a = a * a%mod;
		b >>= 1;
	}
	return res;
}
int main() {
	scanf("%d%d", &n, &K);
	for (int i = 1; i <= n; i++) {
		int x;
		scanf("%d", &x);
		pos[x].push_back(i);
	}
	for (int i = 1; i <= n; i++) {
		if (pos[i].empty())continue;
		vc[i].push_back(pos[i][0]);
		for (int j = 1; j < (int)pos[i].size(); j++) {
			vc[i].push_back(pos[i][j] - pos[i][j - 1]);
		}
		vc[i].push_back(n + 1 - pos[i].back());
		solve(vc[i]);
	}
	ll ans = 0;
	for (int i = 1; i <= n; i++) {
		ans = (ans + c[i] * Pow(i, K) % mod) % mod;
	}
	printf("%lld\n", ans);
	return 0;
}