https://nanti.jisuanke.com/t/42391
题意:给出两个n* m矩阵,两个矩阵都为1到n* m的一种排列,求两个矩阵的最大相同子矩阵。
对于第二个矩阵的每一个位置,仅当相邻点在第一个矩阵中也相邻,才能拓展,处理出该点向由拓展出的最远长度。
则变为如下图,有一些线段,求最大矩形。
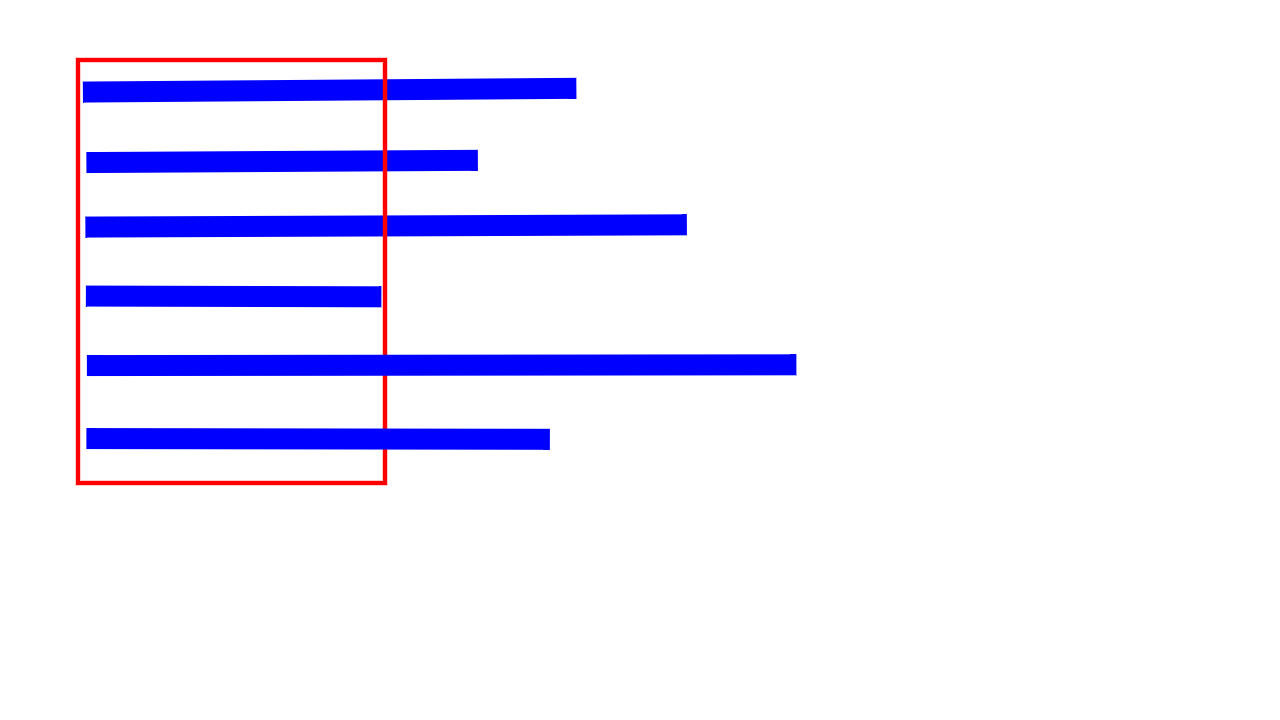
我们可以一列一列地枚举,但对于每一列,只能线性地求最大矩阵。
可以建立一个单调栈,由上到下地放入线段,初始时把第一个线段放进栈中。仅当下一条线段的长度比栈顶长或一样长时,栈顶线段可以继续向下拓展。否则对栈顶线段进行结算并弹出。
还有一种不合法的情况,由于预处理只判断了横向拓展,所以第二个矩阵中同一列的可能在第一个矩阵中并不是同一列,或者第二个矩阵中两行相邻的在第一个矩阵中不相邻,这时要把栈整个清空结算。
注意当弹出栈顶时,预留的空间仍是存在的,因此实际压入栈中的位置也要改变。
最后还要再结算一次。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
| #include<bits/stdc++.h>
using namespace std;
#define ll long long
typedef pair<int, int> pii;
const int INF = 0x3f3f3f3f;
const int maxn = 1e6 + 10;
int n, m;
int a[1010][1010], b[1010][1010];
int dp[1010][1010];
int r[maxn], px[maxn], py[maxn];
stack<int>st;
int ans;
int vis[1010];
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
scanf("%d", &a[i][j]);
px[a[i][j]] = i;
py[a[i][j]] = j;
}
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
scanf("%d", &b[i][j]);
}
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j < m; j++) {
r[a[i][j]] = a[i][j + 1];
}
}
for (int i = 1; i <= n; i++) {
dp[i][m] = 1;
for (int j = m - 1; j >= 1; j--) {
if (r[b[i][j]] == b[i][j + 1]) {
dp[i][j] = dp[i][j + 1] + 1;
}
else dp[i][j] = 1;
}
}
for (int j = 1; j <= m; j++) {
while (!st.empty())st.pop();
fill(vis, vis + n + 1, 0);
for (int i = 1; i <= n; i++) {
if (!st.empty() && (py[b[st.top()][j]] != py[b[i][j]] || !vis[px[b[i][j]] - 1])) {
while (!st.empty()) {
ans = max(ans, dp[st.top()][j] * (i - vis[px[b[st.top()][j]]]));
vis[px[b[st.top()][j]]] = 0;
st.pop();
}
}
int tmp = i;
while (!st.empty() && dp[st.top()][j] > dp[i][j]) {
ans = max(ans, dp[st.top()][j] * (i - vis[px[b[st.top()][j]]]));
tmp = vis[px[b[st.top()][j]]];
st.pop();
}
st.push(i);
vis[px[b[i][j]]] = tmp;
}
while (!st.empty()) {
ans = max(ans, (n + 1 - vis[px[b[st.top()][j]]])*dp[st.top()][j]);
st.pop();
}
}
printf("%d\n", ans);
return 0;
}
|










