http://acm.hdu.edu.cn/contests/contest_show.php?cid=879

1005 - Fibonacci Sum

 

题意：给定 N，C，K，(1≤N,C≤1018,1≤K≤105)(1≤N,C≤10^{18},1≤K≤10^5)，FiF_i 为斐波那契数列的第 i 项。求 (F0)K+(FC)K+(F2C)K+⋯+(FNC)Kmod  1000000009(F_0)^K+(F_C)^K+(F_{2C})^K+\cdots+(F_{NC})^K \mod 1000000009。

二次剩余

几乎是原题了，ZOJ3774

先看原题，求前 N 个斐波那契数的 K 次方和。

数据很大没法矩阵快速幂，只能用通项公式求。

Fi=15[(1+52)i−(1−52)i]F_i=\frac{1}{\sqrt{5}}[(\frac{1+\sqrt{5}}{2})^i-(\frac{1-\sqrt{5}}{2})^i]

5\sqrt{5} 很烦，但是发现模数很奇怪，需要发现 5 是模 1000000009 的二次剩余，也就是说 5\sqrt{5} 是可以用一个整数代替的，那么接下来就可以放心地求了。

令 a=1+52,b=1−52a=\frac{1+\sqrt{5}}{2},b=\frac{1-\sqrt{5}}{2}。

 

则

Fi=15(ai+bi)  ⟹  (Fi)K=(15)K(ai−bi)KF_i=\frac{1}{\sqrt{5}}(a^i+b^i) \implies (F_i)^K=(\frac{1}{\sqrt{5}})^K(a^i-b^i)^K\\

 

二项式展开

(ai−bi)K=(−1)0CK0(ai)K+(−1)1CK1(ai)K−1(bi)1+⋯+(−1)KCKK(bi)K=(−1)0CK0(aK)i+(−1)1CK1(aK−1)i(b1)i+⋯+(−1)KCKK(bK)i\begin{align} (a^i-b^i)^K &= (-1)^0C_K^0(a^i)^K+(-1)^1C_K^1(a^i)^{K-1}(b^i)^1 +\cdots+(-1)^KC_K^K(b^i)^K\\ &= (-1)^0C_K^0(a^K)^i+(-1)^1C_K^1(a^{K-1})^i(b^1)^i+\cdots+(-1)^KC_K^K(b^K)^i\\ \end{align}

 

虽然不能枚举 i，但是可以枚举 CKrC_K^r 中的 r，这样竖着相加每一项，得到 K+1 个 n 项的等比数列求和。

∑i=1N(Fi)K=(15)K∑r=0K∑i=1N[(−1)rCKr(aK−rbr)i]\begin{align} \sum_{i=1}^N (F_i)^K &= (\frac{1}{\sqrt{5}})^K\sum_{r=0}^{K}\sum_{i=1}^{N}[(-1)^r C_K^r(a^{K-r}b^r)^i]\\ \end{align}

 

内层的求和虽然有 N 项，但是可以用等比数列求和公式，预处理出 a，b 的各个幂次，需要时直接用。外层的求和直接枚举。

注意等比数列的公比 aK−rbra^{K-r}b^r 可能为 1，这时和直接就是 N。

代入 a,ba,b 的时候，5\sqrt{5} 用 383008016383008016 代替。得到 a=691504013,b=308495997a=691504013,b=308495997。

以上就是原题的内容了。

再看本题，求第 C 项开始，每隔 C 项取一项，共 N 项的 K 次方和。

在二项式展开这一步有不同

(aiC−biC)K=(−1)0CK0(aiC)K+(−1)1CK1(aiC)K−1(biC)1+⋯+(−1)KCKK(biC)K=(−1)0CK0((aC)K)i+(−1)1CK1((aC)K−1)i((bC)1)i+⋯+(−1)KCKK((bC)K)i\begin{align} (a^{iC}-b^{iC})^K &= (-1)^0C_K^0(a^{iC})^K+(-1)^1C_K^1(a^{iC})^{K-1}(b^{iC})^1 +\cdots+(-1)^KC_K^K(b^{iC})^K\\ &= (-1)^0C_K^0((a^C)^K)^{i}+(-1)^1C_K^1((a^C)^{K-1})^i((b^C)^1)^i+\cdots+(-1)^KC_K^K((b^C)^K)^i\\ \end{align}

可以看到唯一的不同之处就在于 a  ⟹  aC,b  ⟹  bCa\implies a^C,b\implies b^C。

所以在预处理出 a，b 的幂次时多一个 C 即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int N = 100005;
const ll mod = 1000000009;
const int INF = 0x3f3f3f3f;
const ll inf = 0x3f3f3f3f3f3f3f3f;
ll fac[N], A[N], B[N];
ll n, k, c;
ll Pow(ll a, ll b) {
    ll res = 1ll;
    while (b){
        if (b & 1) res = res * a % mod;
        a = a * a % mod;
        b >>= 1;
    }
    return res;
}
void init(){
    A[0] = B[0] = 1ll;
    ll a = Pow(691504013, c);
    ll b = Pow(308495997, c);
    for (int i = 1; i <= k; i++){
        A[i] = A[i - 1] * a % mod;
        B[i] = B[i - 1] * b % mod;
    }
}

ll solve(ll n, ll k){
    ll ans = 0;
    for (int r = 0; r <= k; r++){
        ll t = A[k - r] * B[r] % mod;
        ll x = fac[k];
        ll y = fac[k - r] * fac[r] % mod;
        ll c = x * Pow(y, mod - 2) % mod;
        ll tmp = t * (Pow(t, n) - 1) % mod * Pow(t - 1, mod - 2) % mod;
        if (t == 1) tmp = n % mod;
        tmp = tmp * c % mod;
        if (r & 1) ans -= tmp;
        else ans += tmp;
        ans %= mod;
    }
    ll m = Pow(383008016, mod - 2);
    ans = ans * Pow(m, k) % mod;
    ans = (ans % mod + mod) % mod;
    return ans;
}
int T;
int main(){
    fac[0] = 1;
    for (int i = 1; i < N; i++)
        fac[i] = fac[i - 1] * i % mod;
    scanf("%d", &T);
    while (T--){
        scanf("%lld%lld%lld", &n, &c, &k);
        init();
        printf("%lld\n", solve(n, k));
    }
    return 0;
}

 

1009 - Leading Robots

 

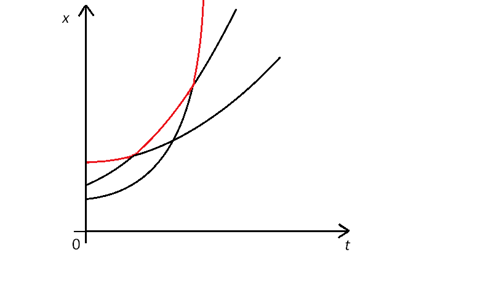
题意：一条跑道上给定 n 个人的距离起点的初始位置 p[i]p[i]，以及他们的加速度 a[i]a[i]，问有多少人在某个时刻能够成为单独的第一名。

单调栈

对所有人按照初始位置从小到大排序，这样每次新遍历到的人一定是可以成为第一名的，所以栈里要维护所有能成为第一名的人。最终人数就是栈的大小。

如果当前栈里只有一个人，那么只要看栈里的人加速度是否大于当前人，大于则一定能追上。

如果栈里至少有2个人，则如上图，假设这3人从下往上序号123，要使这两个人仍然在栈里就必须满足第2个人与第3个人的交点小于第1个人与第3个人的交点。推得 p3−p2a2−a3<p3−p1a1−a3\frac{p_3-p_2}{a_2-a_3}<\frac{p_3-p_1}{a_1-a_3}，但这必须要遍历所有栈里的人，所以还不够，再推 p3−p2a2−a3<p2−p1a1−a2\frac{p_3-p_2}{a_2-a_3}<\frac{p_2-p_1}{a_1-a_2}，这样就可以对栈里每个人维护他和他后面的人的 “斜率”，栈里满足这个 “斜率” 递减。

至于这个式子怎么推出来，还是要熟悉套路吧，先猜结论再证明，之前也是做到过一次类似的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int INF = 0x3f3f3f3f;
const ll inf = 0x3f3f3f3f3f3f3f3f;
const int N = 2e5 + 10;
const ll mod = 1000000007;
int T;
int n;
typedef pair<int, int>pii;
pii a[N];
stack<pii>st;
map<pii, int>mp;
int main(){
	scanf("%d", &T);
	while (T--){
		scanf("%d", &n);
		mp.clear();
		for (int i = 1; i <= n; i++)scanf("%d%d", &a[i].first, &a[i].second);
		for (int i = 1; i <= n; i++)mp[a[i]]++;
		sort(a + 1, a + n + 1);
		for (int i = 1; i <= n; i++) {
			while (!st.empty()) {
				pii t = st.top();
				if (a[i].second >= t.second) {
					st.pop();
					continue;
				}
				if ((int)st.size() == 1) {
					if (t.second <= a[i].second)st.pop();
					else break;
				}
				else {
					st.pop();
					pii q = st.top();
					if (1ll * (a[i].first - t.first)*(q.second - t.second) < 1ll * (t.first - q.first)*(t.second - a[i].second)) {
						st.push(t);
						break;
					}
				}
			}
			st.push(a[i]);
		}
		int ans = (int)st.size();
		while (!st.empty()) {
			if (mp[st.top()] > 1)ans--;
			st.pop();
		}
		printf("%d\n", ans);
	}
	return 0;
}

 

1006 - Finding a MEX

 

题意：给定一张无向图，每点有点权，定义一点的MEX值为所有与该点相邻的点组成的点权集合的MEX值。2种操作：修改某点的点权；查询某点的MEX值。

分块

和重链轻链的思想有些类似。

把所有点按照度的大小分为大点和小点，度>B的为大点。

由于所有点的度数和为2m，所以如果取 B=mB=\sqrt{m} ，则大点的个数为 O(m)O(\sqrt{m})，小点的度为 O(m)O(\sqrt{m})。

对于一个小点，每次的修改操作直接进行，遍历它的所有邻居修改它们的点权集合。

对于一个大点，修改延迟进行，当查询一个点时，修改它的点权集合中的大点。

接下来考虑维护每点的点权集合。

直接维护set查询MEX时肯定超时。如果维护线段树，时间会卡的很紧，每次查询修改都是 log，大概是 O(qmlog⁡n)O(q\sqrt{m}\log n)，写得好也可能卡过。

考虑分块去掉这个log。

由于每次查询时也都会有修改，所以把修改的复杂度降下来更重要。

对于一个点权集合，记录每个数值出现次数，并且按照值域分为根号块，记录每块内不同的数值的个数，每次修改时删除旧数值，添加新数值。由于每点的度最多是 n，所以MEX值最多是 n，所以值域只要维护 0 到 n 即可。

每次查询时，先遍历它的邻居中的大点，O(1)O(1) 修改，更新它的点权集合，再 OnO\sqrt{n} 查询。

这样每次修改是 O(m)O(\sqrt{m})，查询是 O(m+n)O(\sqrt{m}+\sqrt{n})。总的复杂度就是 O(q(m+n))O(q(\sqrt{m}+\sqrt{n})) 。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int INF = 0x3f3f3f3f;
const ll inf = 0x3f3f3f3f3f3f3f3f;
const int N = 2e5 + 10;
const ll mod = 1000000007;
int T;
int n, m, q, a[N], isb[N], B = 300, blo[N];
vector<int>G[N], cnt[N], dif[N];
typedef pair<int, int>pii;
vector<pii>big[N];
void del(int v, int x) {
    if (x > (int)G[v].size())return;
    cnt[v][x]--;
    if (cnt[v][x] == 0)dif[v][x / blo[v]]--;
}
void add(int v, int x) {
    if (x > (int)G[v].size())return;
    cnt[v][x]++;
    if (cnt[v][x] == 1)dif[v][x / blo[v]]++;
}
int main() {
    scanf("%d", &T);
    while (T--) {
        scanf("%d%d", &n, &m);
        for (int i = 1; i <= n; i++) {
            G[i].clear();
            cnt[i].clear();
            dif[i].clear();
            big[i].clear();
            isb[i] = 0;
        }
        for (int i = 1; i <= n; i++) {
            scanf("%d", &a[i]);
        }
        for (int i = 0; i < m; i++) {
            int u, v;
            scanf("%d%d", &u, &v);
            G[u].push_back(v);
            G[v].push_back(u);
        }
        for (int i = 1; i <= n; i++) {
            blo[i] = (int)sqrt((int)G[i].size()) + 1;
            cnt[i].resize(G[i].size() + 1);
            dif[i].resize((G[i].size() / blo[i] + 1));
        }
        for (int i = 1; i <= n; i++) {
            if ((int)G[i].size() > B)isb[i] = 1;
            for (int v : G[i]) {
                if ((int)G[v].size() > B)big[i].push_back(pii(v, a[v]));
            }
        }
        for (int i = 1; i <= n; i++) {
            for (int v : G[i])add(i, a[v]);
        }
        scanf("%d", &q);
        while (q--) {
            int op;
            scanf("%d", &op);
            if (op == 1) {
                int u, x;
                scanf("%d%d", &u, &x);
                if (!isb[u]) {
                    for (int v : G[u]) {
                        del(v, a[u]);
                        add(v, x);
                    }
                }
                a[u] = x;
            }
            else {
                int u;
                scanf("%d", &u);
                for (pii& p : big[u]) {
                    if (p.second != a[p.first]) {
                        del(u, p.second);
                        add(u, a[p.first]);
                        p.second = a[p.first];
                    }
                }
                int C = (int)ceil((double)G[u].size() / blo[u]);
                for (int i = 0; i <= C; i++) {
                    if (dif[u][i] != blo[u]) {
                        for (int j = 0; j < blo[u]; j++) {
                            if (!cnt[u][i*blo[u] + j]) {
                                printf("%d\n", i*blo[u] + j);
                                break;
                            }
                        }
                        break;
                    }
                }
            }
        }
    }
    return 0;
}