https://ac.nowcoder.com/acm/contest/5673#question

E - Enigmatic Partition

 

题意：给定 n，要求分解为几个非递减的数的和，并且相邻数的差不超过 1，且最后一个数 - 第一个数 = 2.

做法一：枚举。

题解的做法。

设 n=nl∗l+m∗mid+nr∗rn=nl*l+m*mid+nr*r。因为 l=mid−1=r−2l=mid-1=r-2。所以每两个 midmid 可以分解为 1 个 ll + 1 个 rr，共有 mm 个 midmid，则共有 ⌊(m−1)/2⌋\lfloor (m-1)/2 \rfloor 种分解情况，-1 是因为至少要留一个 midmid。

枚举 ll，再分两种情况：nl>nrnl>nr 和 nl≤nrnl\le nr，由于分解 midmid 不会改变两者的大小关系，所以这两种情况没有交集。对于第一种情况，枚举 nl−nrnl-nr，即多出的个数，再枚举 mm，这样就确定到了单个的 nn，这个 nn 的答案 +=⌊(m−1)/2⌋+=\lfloor (m-1)/2 \rfloor 即可。

但是由于一个 nn 可能有多种 nl,l,m,mid,nr,rnl,l,m,mid,nr,r 的组合情况，所以必然被枚举多次，所以复杂度很高。

题解说的是需要dp优化 l≤100l\le100 的情况。

 

做法二：差分。

参考了 大佬博客。

a = 1, m = 7

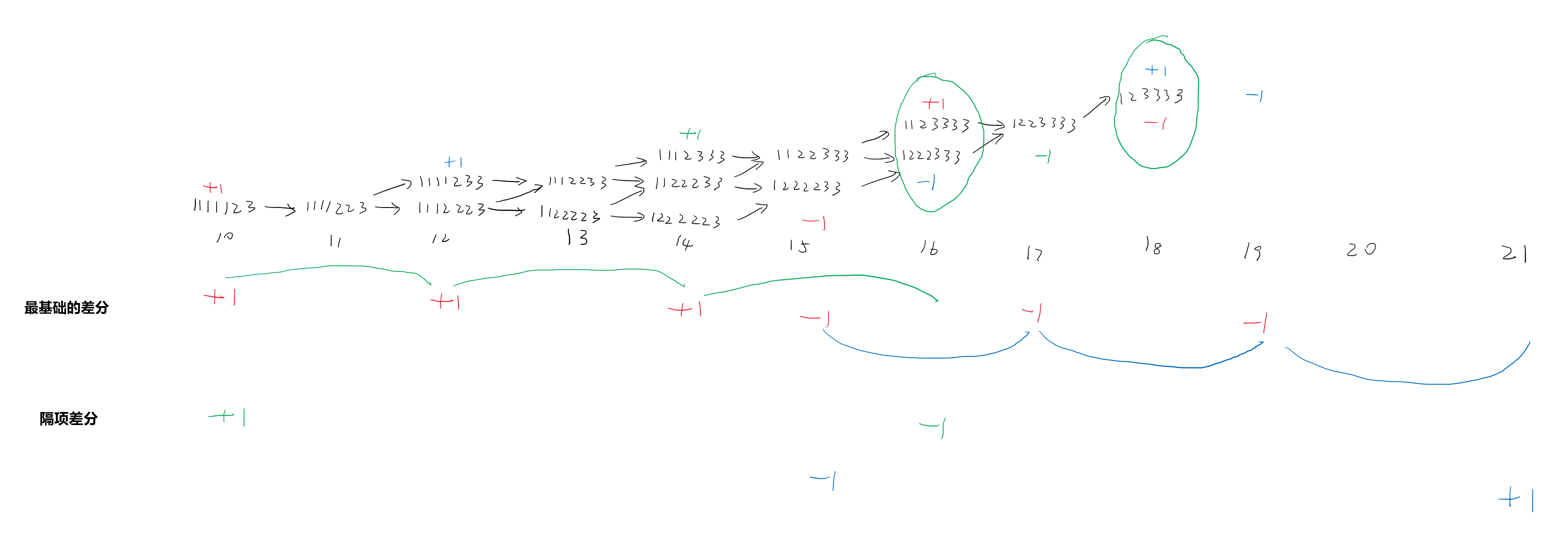
枚举第一个数 aa，以及总个数 mm。如上图 a=1,m=7a=1,m=7。得到几层区间加，对这些区间加先处理出最基本的差分，由于这些差分个数还是很多，所以再处理一次。观察发现最基础的差分先是隔项有一个 +1，再是隔项有一个 -1，所以用隔项差分处理，所谓隔项差分也就是两个差分拼在一起，在本题每一个都是当前项与隔一项后的一项在一起差分。处理完变成了两个差分，每个只要处理头和尾即可。

第一个差分的头就是开始位置，尾在 a,a+1,a+1,a+1,⋯ ,a+1,a+2a,a+1,a+1,a+1,\cdots,a+1,a+2 处，因为后面就没有斜着向上的箭头了，也就没法再增加一层了。

第二个差分的头在 a,a+1,a+1,a+1,⋯ ,a+1,a+2a,a+1,a+1,a+1,\cdots,a+1,a+2 后一个，因为从这里起就没有第一层区间加了，尾在 a,a+1,a+2,⋯ ,a+2a,a+1,a+2,\cdots,a+2，因为后面就没有了。

本题最关键的在于要能发现这个规律，想到枚举 a 和 m，并且能按照上图的箭头方式枚举，再把每一层视为一个区间加，想到差分，差分之后再差分。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int INF = 0x3f3f3f3f;
const int N = 1e5 + 10;
const ll mod = 998244353;
int T;
ll f[N << 4];
int main() {
	scanf("%d", &T);
	for (int a = 1; a < N; a++) {
		for (int m = 3; m * a < N; m++) {
			f[a*(m - 2) + a + 1 + a + 2]++;
			f[(a + 1)*m + 1]--;
			f[(a + 1)*m + 2]--;
			f[(a + 2)*(m - 2) + a + a + 1 + 3]++;
		}
	}
	for (int i = 2; i < N; i++)f[i] += f[i - 2];
	for (int i = 2; i < N; i++)f[i] += f[i - 1];
	for (int i = 2; i < N; i++)f[i] += f[i - 1];
	for (int i = 1; i <= T; i++) {
		int l, r;
		scanf("%d%d", &l, &r);
		printf("Case #%d: %lld\n", i, f[r] - f[l - 1]);
	}
	return 0;
}

 

A - All-Star Game

 

题意：给定 nn 个球员，mm 个粉丝，以及喜爱关系。多次修改，每次给出一个关系，若已经存在，则去除，否则添加。一个粉丝会看比赛当且仅当：他喜爱的球员在比赛中，或另一个与他喜爱某个相同球员的粉丝看比赛。问每次修改后，比赛中至少要有几个球员，才能保证所有粉丝都看比赛。

线段树+可撤销并查集

把有关系的球员和粉丝相连，画下样例就能发现，每个联通块只要出一个球员即可，而那些只有球员的联通块一个都不需要出，而若存在只有粉丝的联通块，则无解。

所以就是先判断是否存在只有粉丝的连通块，若存在则无解，若不存在，则答案为 总连通块数 - 只包含球员的连通块数。

加边和删边的同时需要计算连通块。无法直接模拟，因为不知道删完一条边后这两个端点是否还连通。那么就要想能否离线。

线段树以时间作为下标，一条边在一个时间区间中是连上的，那么就在线段树上的这个区间相对应的节点上都加上这条边，当离开这些节点时，可撤销并查集撤回到进入之前的状态。

用 “撤销加边” 来代替 “删边”，这就是本题直接并查集模拟行不通而 线段树+可撤销并查集就可行的原因。

在实现的时候，由于一个节点可能要加上多条边，所以要用栈保存加边之前的状态以便撤销。但是本题空间很紧，栈的空间开销比vector大，会导致MLE，所以要用vector模拟栈。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
#include <bits/stdc++.h>
#define debug(x) cout << #x << ":\t" << (x) << endl;
using namespace std;
#define ll long long
#define ull unsigned ll
const int N = 4e5 + 5;
const int INF = 0x3f3f3f3f;
const ll inf = 0x3f3f3f3f3f3f3f3f;
const ll mod = 1e9 + 7;
const ll inv2 = (mod + 1) / 2;
int n, m, q;
struct E
{
	int u, v;
};
map<int, int>mp[N];
#define mid ((l+r)>>1)
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
vector<E>vc[N << 2];
void upd(int ql, int qr, E e, int l, int r, int rt) {
	if (ql <= l && qr >= r) {
		vc[rt].push_back(e);
		return;
	}
	if (ql <= mid)upd(ql, qr, e, lson);
	if (qr > mid)upd(ql, qr, e, rson);
}

int par[N], rk[N], siz[N];
void init(int n) {
	for (int i = 1; i <= n; i++) {
		par[i] = i;
		rk[i] = 1;
		siz[i] = 1;
	}
}
int find(int x) { return par[x] == x ? x : find(par[x]); }
void unit(int x, int y) {
	x = find(x); y = find(y);
	if (x == y)return;
	if (rk[x] < rk[y]) {
		par[x] = y;
		siz[y] += siz[x];
	}
	else {
		par[y] = x;
		siz[x] += siz[y];
		if (rk[x] == rk[y])rk[x]++;
	}
}
struct X
{
	int u, v;
	int rku, rkv, sizu, sizv;
	int cntt, cntp, cntf;
};
vector<X>st[N << 2];
int ans[N];
int cntt, cntp, cntf;
void dfs(int l, int r, int rt) {
	for (E& e : vc[rt]) {
		int u = find(e.u), v = find(e.v);
		if (u == v)continue;
		st[rt].push_back({ u,v,rk[u],rk[v],siz[u],siz[v],cntt,cntp,cntf });
		cntt--;
		if (siz[u] == 1) {
			if (u <= n)cntp--;
			else cntf--;
		}
		if (siz[v] == 1) {
			if (v <= n)cntp--;
			else cntf--;
		}
		unit(u, v);
	}
	if (l == r) {
		if (cntf)ans[l] = -1;
		else ans[l] = cntt - cntp;
	}
	else {
		dfs(lson);
		dfs(rson);
	}
	while (!st[rt].empty()) {
		X x = st[rt].back(); st[rt].pop_back();
		par[x.u] = x.u; par[x.v] = x.v;
		siz[x.u] = x.sizu; siz[x.v] = x.sizv;
		rk[x.u] = x.rku; rk[x.v] = x.rkv;
		cntt = x.cntt; cntf = x.cntf; cntp = x.cntp;
	}
}
int main() {
	scanf("%d%d%d", &n, &m, &q);
	for (int i = 1; i <= n; i++) {
		int k, x;
		scanf("%d", &k);
		for (int j = 1; j <= k; j++) {
			scanf("%d", &x);
			mp[i][x] = 1;
		}
	}
	for (int i = 2; i <= q + 1; i++) {
		int x, y;
		scanf("%d%d", &y, &x);
		if (mp[x].count(y) && mp[x][y]) {
			upd(mp[x][y], i - 1, { x,y + n }, 1, q + 1, 1);
			mp[x][y] = 0;
		}
		else {
			mp[x][y] = i;
		}
	}
	for (int i = 1; i <= n; i++) {
		for (auto p : mp[i]) {
			if (p.second)upd(p.second, q + 1, { i,p.first + n }, 1, q + 1, 1);
		}
	}
	init(n + m);
	cntt = n + m;
	cntp = n; cntf = m;
	dfs(1, q + 1, 1);
	for (int i = 2; i <= q + 1; i++)printf("%d\n", ans[i]);
	return 0;
}