https://ac.nowcoder.com/acm/contest/5672

J - Pointer Analysis

 

题意：给定了一段程序，有种操作，26个object用小写字母表示，26个全局指针用大写字母表示，每个object也有26个成员指针变量也用小写字母表示，程序会不断重复执行，且执行顺序随机，问最终每个全局指针指向的object。

模拟

P[A][a]P[A][a] 表示全局指针 A 是/否 指向object a。

O[a][b][c]O[a][b][c] 表示object a 的 成员指针 b 是/否 指向object c。

接下来直接暴力模拟即可。

要注意的是由于不断随机顺序执行，所以对与每个语句要执行所有可能的情况，所以最外层要迭代 n 次。迭代 n 次就可以得到所有情况了，把程序复制n次排下去，可以发现任意排列都可以在新的程序中找到（每段里选一句即可）。若少于 n 次则必定缺少，比如倒序。

对此还需要注意的是只有当所有语句都是重复执行不影响结果时才可以。

比如

1
2
3
4
A++;
B = A;
B = A;
A++;
1
2
3
4
A++;
B = A;
B = A;
A++;

上面两个显然不一样，因为 A++ 重复执行会影响结果，即执行一次与两次会导致 A 的结果不同，这时就不行。

而如果满足这个条件，则只要保证两两之间的顺序满足，执行次数就不需要注意了。这一点在操作系统的日志部分似乎有学过。

本题所有赋值语句显然都满足条件，所以可以使用。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int INF = 0x3f3f3f3f;
const ll inf = 0x3f3f3f3f3f3f3f3f;
const int N = 2e6 + 10;
const ll mod = 1e9 + 7;
int n;
bool P[30][30], O[30][30][30];
char s1[210][10], s2[210][10];
int main() {
	scanf("%d", &n);
	for (int i = 0; i < n; i++)scanf("%s = %s", s1[i], s2[i]);
	for (int it = 0; it < n; it++) {
		for (int i = 0; i < n; i++) {
			char c = s1[i][0], p = s2[i][0];
			int l1 = (int)strlen(s1[i]), l2 = (int)strlen(s2[i]);
			if (l1 == 1 && l2 == 1) {
				if (islower(p)) {
					P[c - 'A'][p - 'a'] = 1;
				}
				else {
					for (int k = 0; k < 26; k++) {
						P[c - 'A'][k] |= P[p - 'A'][k];
					}
				}
			}
			else if (l1 == 3) {
				for (int k = 0; k < 26; k++) {
					if (!P[c - 'A'][k])continue;
					for (int x = 0; x < 26; x++) {
						if (P[p - 'A'][x]) {
							O[k][s1[i][2] - 'a'][x] = 1;
						}
					}
				}
			}
			else {
				for (int k = 0; k < 26; k++) {
					if (!P[p - 'A'][k])continue;
					for (int x = 0; x < 26; x++) {
						if (O[k][s2[i][2] - 'a'][x]) {
							P[c - 'A'][x] = 1;
						}
					}
				}
			}
		}
	}
	for (int i = 0; i < 26; i++) {
		printf("%c: ", 'A' + i);
		for (int j = 0; j < 26; j++)if (P[i][j])printf("%c", 'a' + j);
		puts("");
	}
	return 0;
}

 

C - A National Pandemic

 

题意：给定一棵树，三种操作：在点 u 上权值 +w，在其它点 v 权值 +w-dist(u, v)；若点 u 权值大于 0，则变为 0，否则不变；查询点 u 的权值。

树链刨分+树状数组

w−dist(u,v)=w−(dep[u]+dep[v]−2⋅dep[lca])=w−dep[u]−dep[v]+2⋅dep[lca]w-dist(u,v)=w-(dep[u]+dep[v]-2\cdot dep[lca])=w-dep[u]-dep[v]+2\cdot dep[lca]

对于每次询问，w,dep[u],dep[v]w,dep[u],dep[v] 都可以用全局变量维护，唯一需要查询的是 lca，但是由于有很多个已经修改过的点，也就有很多个 lca，所以必然不能直接查询，所以还是要维护所有的 dep 之和。

树链刨分，则每次查询最多跳log条链，对于每条链单独维护两个树状数组，一个记录链上修改的点的dep之和，另一个记录修改的点的个数。

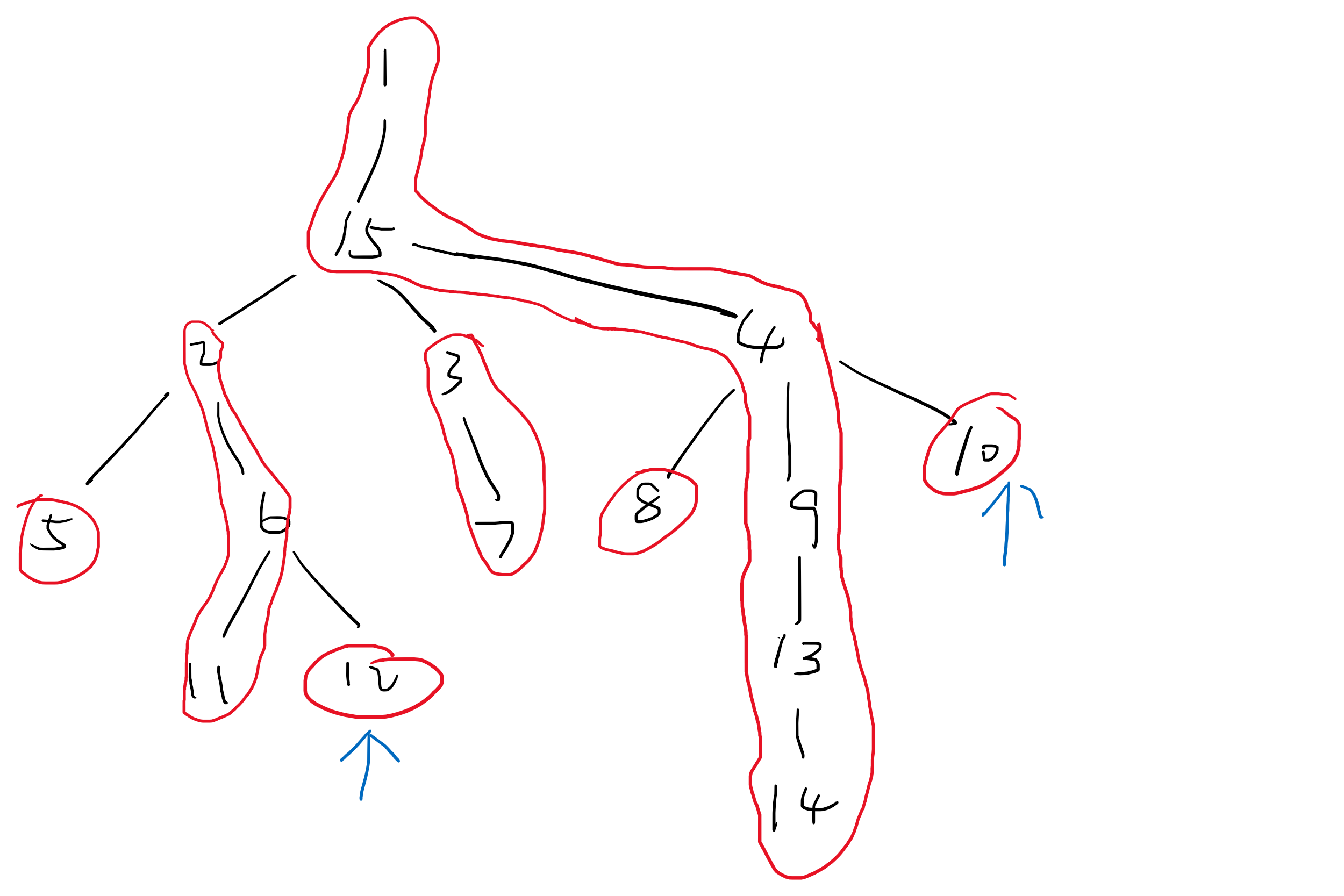
对于每次修改操作，从点 u 起一直向上跳链，每次修改所在链上的两个树状数组。

对于每次查询操作，同样从点 u 起一直向上跳链，如上图，假设查询 12，目前已经修改过 10，则 lca 为 15，修改 10 时从 10 起跳链，1 到 14 这条链其中一个树状数组上 4 的位置 +dep[4]，另一个树状数组 4 的位置上计数 +1。查询 12 时从 12 起跳链，在 2 到 6这条链上无事发生，再跳到 1 到 14 这条链，此时链上在 4 处有修改，但是此时跳到的位置是 15，所以树状数组用前缀和得到 15 以下的计数，这些计数的修改点与 12 的 lca 必定是15，所以只要 计数*dep[15] 就是 lca 为 15 时的贡献，当然还可能有 lca 为 1 时的贡献，所以用到另一个树状数组，找到链上 15 以上的部分的 dep 之和。

这样就得到了所有的 dep[lca]dep[lca]，再加上 ∑w+∑dep[v]+c⋅dep[u]\sum w+\sum dep[v]+c\cdot dep[u]，其中 v 为修改过的点，c 为修改操作的次数。

但是由于操作 2 可以清除某点的权值，所以还要设置一个 del[u]del[u]，查询时用上面计算得到的 res 加上 del[u]del[u] 得到真正的结果。

当执行操作 2 时，由于真正的结果是 res+del[u]res+del[u]，所以如果该值大于 0，则应该变为 0，所以 del[u]del[u] 要变为 −res-res。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int INF = 0x3f3f3f3f;
const ll inf = 0x3f3f3f3f3f3f3f3f;
const int N = 2e5 + 10;
const ll mod = 1e9 + 7;
int T;
int n, m;
vector<int>G[N];
int siz[N], fa[N], dep[N], son[N], topf[N];
vector<int>link[N];
void dfs1(int u, int _fa) {
	siz[u] = 1; fa[u] = _fa;
	for (int v : G[u]) {
		if (v == _fa)continue;
		dep[v] = dep[u] + 1;
		dfs1(v, u);
		siz[u] += siz[v];
		if (siz[v] > siz[son[u]])son[u] = v;
	}
}
void dfs2(int u, int topfa) {
	topf[u] = topfa;
	link[topfa].push_back(u);
	if (!son[u])return;
	dfs2(son[u], topfa);
	for (int v : G[u]) {
		if (!topf[v])dfs2(v, v);
	}
}
int num[N];
ll sw, sd, sc;
int lowbit(int x) { return x & -x; }
vector<int>sumc[N];
vector<ll>sumd[N];
void addc(int id, int p) {
	for (int i = p; i < (int)sumc[id].size(); i += lowbit(i)) {
		sumc[id][i]++;
	}
}
void addd(int id, int p, int x) {
	for (int i = p; i < (int)sumd[id].size(); i += lowbit(i)) {
		sumd[id][i] += x;
	}
}
int qryc(int id, int r) {
	int res = 0;
	for (int i = r; i > 0; i -= lowbit(i)) {
		res += sumc[id][i];
	}
	return res;
}
ll qryd(int id, int r) {
	ll res = 0;
	for (int i = r; i > 0; i -= lowbit(i)) {
		res += sumd[id][i];
	}
	return res;
}
void add(int u) {
	while (u) {
		addc(topf[u], num[u]);
		addd(topf[u], num[u], dep[u]);
		u = fa[topf[u]];
	}
}
ll del[N];
ll qry(int s) {
	ll res = 0; int pre = 0;
	int u = s;
	while (u) {
		int topfa = topf[u];
		res += 1ll * dep[u] * (qryc(topfa, num[u]) - pre);
		res += qryd(topfa, num[topfa]) - qryd(topfa, num[u]);
		pre = qryc(topfa, num[topfa]);
		u = fa[topfa];
	}
	res = sw - sd - 1ll*sc * dep[s] + 2 * res;
	return res;
}
int main() {
	scanf("%d", &T);
	while (T--) {
		scanf("%d%d", &n, &m);
		sw = sd = sc = 0;
		for (int i = 1; i <= n; i++) {
			G[i].clear();
			son[i] = 0;
			link[i].clear();
			sumc[i].clear();
			sumd[i].clear();
			topf[i] = 0;
			del[i] = 0;
		}
		for (int i = 1; i < n; i++) {
			int u, v;
			scanf("%d%d", &u, &v);
			G[u].push_back(v);
			G[v].push_back(u);
		}
		dfs1(1, 0);
		dfs2(1, 1);
		for (int i = 1; i <= n; i++) {
			if (link[i].empty())continue;
			int sz = (int)link[i].size();
			sumc[i].resize(sz + 1);
			sumd[i].resize(sz + 1);
			for (int j = 0; j < sz; j++) {
				num[link[i][j]] = sz - j;
			}
		}
		while (m--) {
			int op, u, w;
			scanf("%d", &op);
			if (op == 1) {
				scanf("%d%d", &u, &w);
				add(u);
				sw += w;
				sd += dep[u];
				sc++;
			}
			else if (op == 2) {
				scanf("%d", &u);
				ll res = qry(u);
				if (res + del[u]> 0)del[u] = -res;
			}
			else {
				scanf("%d", &u);
				printf("%lld\n", qry(u) + del[u]);
			}
		}
	}
	return 0;
}

 

A - Social Distancing

 

题意：在二维平面上要找 nn 个格点，满足与原点距离不超过 rr，且 ∑i=1n−1∑j=i+1ndist(i,j)2\sum_{i=1}^{n-1}\sum_{j=i+1}^{n}dist(i,j)^2 最大。多次询问。

dp

平方和不好处理，先推式子。

(x1−x2)2+(x2−x3)2+(x1−x3)2=2(x12+x22+x32)−2x1x2−2x1x3−2x2x3=3(x12+x22+x32)−(x1+x2+x3)2\begin{align} &(x_1-x_2)^2+(x_2-x_3)^2+(x_1-x_3)^2\\ &=2(x_1^2+x_2^2+x_3^2)-2x_1x_2-2x_1x_3-2x_2x_3\\ &=3(x_1^2+x_2^2+x_3^2)-(x_1+x_2+x_3)^2\\ \end{align}

以此类推

∑i=1n−1∑j=i+1n(xi−xj)2=n⋅∑i=1nxi2−(∑i=1nxi)2\sum_{i=1}^{n-1}\sum_{j=i+1}^{n}(x_i-x_j)^2=n\cdot\sum_{i=1}^{n}x_i^2-(\sum_{i=1}^n x_i)^2\\

所以

∑i=1n−1∑j=i+1ndist(i,j)2=n⋅∑i=1n(xi2+yi2)−(∑i=1nxi)2−(∑i=1nyi)2\sum_{i=1}^{n-1}\sum_{j=i+1}^{n}dist(i,j)^2=n\cdot\sum_{i=1}^{n}(x_i^2+y_i^2)-(\sum_{i=1}^n x_i)^2-(\sum_{i=1}^n y_i)^2\\

设 dp[i][j][k]dp[i][j][k] 表示 ii 个点，横坐标之和为 jj，纵坐标之和为 kk ，最大 ∑i=1n(xi2+yi2)\sum_{i=1}^{n}(x_i^2+y_i^2) 值。

ans[n][r]ans[n][r] 表示 nn 个点，与原点距离不超过 rr 的答案。

数据范围很小，可以直接枚举所有点更新答案。

以与原点距离 rr 递增枚举所有格点，更新 dpdp 同时计算答案 ansans。

cf上有道原题 Roland and Rose，但是是单个询问，所以直接枚举凸包上的点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
#include <bits/stdc++.h>
#define debug(x) cout << #x << ":\t" << (x) << endl;
using namespace std;
#define ll long long
#define ull unsigned ll
const int N = 4e5 + 5;
const int INF = 0x3f3f3f3f;
const ll inf = 0x3f3f3f3f3f3f3f3f;
const ll mod = 1e9 + 7;
const ll inv2 = (mod + 1) / 2;
int T;
typedef pair<int, int>pii;
typedef pair<int, pii>ppii;
vector<ppii>vc;
const int base = 300;
int dp[10][1010][1010], ans[10][100];
int main() {
	scanf("%d", &T);
	for (int i = -30; i <= 30; i++) {
		for (int j = -30; j <= 30; j++) {
			vc.push_back({ i*i + j * j,{i,j} });
		}
	}
	sort(vc.begin(), vc.end(),greater<ppii>());
	for (int i = 0; i <= 8; i++)for (int j = 0; j <= 600; j++)for (int k = 0; k <= 600; k++)dp[i][j][k] = -INF;
	dp[0][base][base] = 0;
	for (int r = 1; r <= 30; r++) {
		while (!vc.empty() && vc.back().first <= r * r) {
			int x = vc.back().second.first, y = vc.back().second.second, xy = vc.back().first;
			vc.pop_back();
			for (int i = 1; i <= 8; i++) {
				for (int j = base - r * i; j <= base + r * i; j++) {
					for (int k = base - r * i; k <= base + r * i; k++) {
						dp[i][j][k] = max(dp[i][j][k], dp[i - 1][j - x][k - y] + xy);
						if (dp[i][j][k] > 0)ans[i][r] = max(ans[i][r], dp[i][j][k] * i - (j - base)*(j - base) - (k - base)*(k - base));
					}
				}
			}
		}
	}
	while (T--) {
		int n, r;
		scanf("%d%d", &n, &r);
		printf("%d\n", ans[n][r]);
	}
	return 0;
}

 

I - Valuable Forests

 

题意：求所有 nn 个有标号点的无根树上度数的平方和。∑u∈V(d[u])2\sum_{u\in V}(d[u])^2。

prufer序列+dp

设 f[i]f[i] 表示 ii 个有标号点组成森林，的方案数。

g[i]g[i] 表示一棵有 ii 个有标号点的无根树上点的度数的平方和。

求 f[i]f[i]：dp，枚举当前这棵树的大小。根据Cayley定理，有 nn 个标号点的无根树有 nn−2n^{n-2} 种。且由于标号不确定，所以还要从 [1,i][1,i] 中选择，但是为了保证不重复，必须规定 ii 一定被选中，所以从 [1,i−1][1,i-1] 中选 j−1j-1 个标号。

f[0]=f[1]=1f[i]=∑j=1if[i−j]⋅jj−2⋅Ci−1j−1f[0]=f[1]=1\\ f[i]=\sum_{j=1}^if[i-j]\cdot j^{j-2}\cdot C_{i-1}^{j-1}\\

求 g[i]g[i]：枚举每个点计算它的贡献。对于点 uu，枚举它的度数 jj，根据 prufer 序列，构造一棵树相当于构造这个长度为 n−2n-2 的序列，而序列中 uu 的出现次数等于 uu 的度数-1，所以相当于求 n−2n-2 的序列中 j−1j-1 个位置为 uu，其它位置为 [1,i][1,i] 中非 uu 的方案数。每个点的贡献相同，所以乘以 ii 就是总贡献。

g[i]=i⋅∑j=1i−1j2⋅Ci−2j−1⋅(i−1)i−j−1g[i]=i\cdot\sum_{j=1}^{i-1}j^2\cdot C_{i-2}^{j-1}\cdot (i-1)^{i-j-1}\\

求答案 ans[i]ans[i]：与求 ff 类似。dp，枚举当前这棵树的大小 jj。则 ans[i−j]ans[i-j] 的方案数等于当前这棵树的形态数 jj−2j^{j-2}，当前这棵树的度数平方和 g[j]g[j] 的方案数等于 i−ji-j 个点组成森林的方案数 f[i−j]f[i-j]。又由于标号未确定，所以要选择标号，同样为了不重复，ii 必须选。

ans[i]=∑j=1i(ans[i−j]⋅jj−2+g[j]⋅f[i−j])×Ci−1j−1ans[i]=\sum_{j=1}^i(ans[i-j]\cdot j^{j-2}+g[j]\cdot f[i-j])\times C_{i-1}^{j-1}\\

要预处理幂次与组合数，注意幂次小于零的情况。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
#include <bits/stdc++.h>
#define debug(x) cout << #x << ":\t" << (x) << endl;
using namespace std;
#define ll long long
#define ull unsigned ll
const int N = 2e6 + 5;
const int INF = 0x3f3f3f3f;
const ll inf = 0x3f3f3f3f3f3f3f3f;
ll mod = 1e9 + 7;
const ll inv2 = (mod + 1) / 2;
int T;
ll pw[5010][5010];
ll f[N], g[N], ans[N], C[5010][5010];
ll Pow(int a, int b) {
	if (a == 1)return 1;
	return pw[a][b];
}
int main() {
	scanf("%d%lld", &T, &mod);
	for (int i = 0; i <= 5000; i++)C[i][i] = C[i][0] = 1;
	for (int i = 2; i <= 5000; i++) {
		for (int j = 1; j <= 5000; j++) {
			C[i][j] = (C[i - 1][j - 1] + C[i - 1][j]) % mod;
		}
	}
	for (int i = 1; i <= 5000; i++) {
		pw[i][0] = 1;
		for (int j = 1; j <= 5000; j++)pw[i][j] = pw[i][j - 1] * i%mod;
	}
	f[0] = f[1] = 1;
	for (int i = 2; i <= 5000; i++) {
		for (int j = 1; j <= i; j++) {
			f[i] = (f[i] + f[i - j] * Pow(j, j - 2) % mod*C[i - 1][j - 1] % mod) % mod;
		}
	}
	for (int i = 1; i <= 5000; i++) {
		for (int j = 1; j <= i - 1; j++) {
			g[i] = (g[i] + 1ll * i*j*j%mod*C[i - 2][j - 1] % mod*Pow(i - 1, i - j - 1) % mod) % mod;
		}
	}
	for (int i = 2; i <= 5000; i++) {
		for (int j = 1; j <= i; j++) {
			ans[i] = (ans[i] + (ans[i - j] * Pow(j, j - 2) % mod + g[j] * f[i - j] % mod)*C[i - 1][j - 1] % mod) % mod;
		}
	}
	while (T--) {
		int n;
		scanf("%d", &n);
		printf("%lld\n", ans[n]);
	}
	return 0;
}