https://codeforces.com/contest/1174
D. Ehab and the Expected XOR Problem
题意:给定数n和x,要求构造一个尽可能长的数组,任意区间内的异或和不等于0或x。
遇到区间还是要变成前缀和。问题变为构造n个不相等的数,两两异或不为x。
所以直接筛就好了,从前到后遍历,遇到没删的就取,然后删掉x异或的值。
可以发现这么做最终一定剩下一半的数,并且这是最多的情况。
得到了前缀和,直接构造即可。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
| #include<bits/stdc++.h>
using namespace std;
#define ll long long
const int INF = 0x3f3f3f3f;
const ll inf = 0x3f3f3f3f3f3f3f3f;
const int N = 1e6 + 10;
const ll mod = 1e9 + 7;
int n, x;
int die[N];
vector<int>ans;
int main() {
scanf("%d%d", &n, &x);
for (int i = 1; i < (1 << n); i++) {
if (die[i] || i == x)continue;
ans.push_back(i);
die[x^i] = 1;
}
printf("%d\n", (int)ans.size());
if (ans.empty())return 0;
printf("%d", ans[0]);
for (int i = 1; i < (int)ans.size(); i++) {
printf(" %d", ans[i] ^ ans[i - 1]);
}
puts("");
return 0;
}
|
E. Ehab and the Expected GCD Problem
题意:给定n,对于一个n的排列p,f§ 为p的n个前缀gcd中不相同值的个数。问n的排列中有几个排列的f§=f§max。
dp
参考 https://www.cnblogs.com/1000Suns/p/10987188.html
首先要知道 f§max。由于是前缀,所以后面的gcd都是第一个数的因子,那么自然想到第一个数因子越多越好,再试几个就能发现,后面的gcd是前面的去掉一个质因子,所以第一个数的质因子个数要最多。
如果第一个数包含质因子5,那么可以换成 22,质因子个数变多了,且还符合条件。所以第一个数不能含有大于3的质因子,也就是说 p[0]=2x3y。后面的gcd等于前面的gcd去掉一个质因子(即2或3)。
然后就是dp。
dp[i][x][y] 表示到第 i 位,gcd=2x3y ,的方案数。
考虑 p[0] 如果包含 32,则可以换成 23,质因子数更多。所以 p[0] 最多含有一个3,那么 y 只能为0或1。
有三种转移:
- gcd不变,仍为 2x3y,第i位可以填包含gcd的数,即n以内 2x3y 的倍数,注意要去掉前i-1位填过的,前i-1位都包含gcd,则 dp[i][x][y]=dp[i−1][x][y]⋅(⌊2x3yn⌋−(i−1))。
- gcd中去掉一个2,第i位可以填 2x−13y 的倍数,注意要去掉 2x3y 的倍数。则 dp[i][x][y]=dp[i−1][x−1][y]⋅(⌊2x−13yn⌋−⌊2x3yn⌋)。
- gcd中去掉一个3,与2类似,dp[i][x][y]=dp[i−1][x][y−1]⋅(⌊2x3y−1n⌋−⌊2x3yn⌋)。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
| #include<bits/stdc++.h>
using namespace std;
#define ll long long
const int INF = 0x3f3f3f3f;
const ll inf = 0x3f3f3f3f3f3f3f3f;
const int N = 1e6 + 10;
const ll mod = 1e9 + 7;
int n;
int cnt(int x, int y) {
int res = (1 << x);
if (y)res *= 3;
return n / res;
}
int dp[N][21][2];
int main() {
scanf("%d", &n);
int m = (int)log2(n);
dp[1][m][0] = 1;
if ((1 << (m - 1)) * 3 <= n)dp[1][m - 1][1] = 1;
for (int i = 2; i <= n; i++) {
for (int j = 0; j <= m; j++) {
for (int k = 0; k <= 1; k++) {
dp[i][j][k] = 1ll*dp[i - 1][j][k] * (cnt(j, k) - (i - 1)) % mod;
if (j + 1 <= m)
dp[i][j][k] = (dp[i][j][k] + 1ll*dp[i - 1][j + 1][k] * (cnt(j, k) - cnt(j + 1, k)) % mod) % mod;
if (k == 0)
dp[i][j][k] = (dp[i][j][k] + 1ll*dp[i - 1][j][k + 1] * (cnt(j, k) - cnt(j, k + 1)) % mod) % mod;
}
}
}
printf("%d\n", dp[n][0][0]);
return 0;
}
|
F. Ehab and the Big Finale
题意:交互题。给定一棵树,要猜一个节点,两种询问:第一种返回问的节点与要猜节点的距离,第二种返回问的节点与要猜节点的路径上第二个节点。第二种询问要求问的节点必须是要猜节点的祖先。询问次数小于36。
树链刨分
必须保证 logn,所以要考虑树刨,因为重链的段数为logn。
对于当前节点u,要找到u的重链上最深的那个节点v。
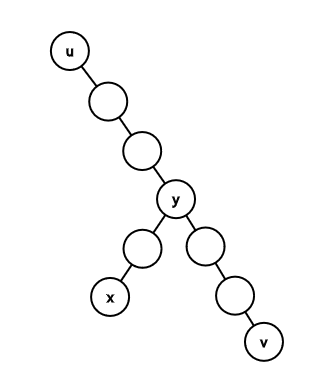
然后找到v与x的LCA y。然后判断,如果x在uv这条链上,那么y=x。否则要跳轻链了。
通过第一种询问可以得到xv的距离,因为预先能问出x的深度,以及预处理出v的深度,所以也就能确定y的深度,由于y一定是x的祖先,所以只要判断xy深度是否相同就能知道是否x=y。
否则通过第二种操作得到下一个当前节点,跳到下一条重链上。
由于重链 logn 条,每次询问问两种,且一定跳一条,所以为 2logn。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
| #include<bits/stdc++.h>
using namespace std;
#define ll long long
const int INF = 0x3f3f3f3f;
const ll inf = 0x3f3f3f3f3f3f3f3f;
const int N = 1e6 + 10;
const ll mod = 1e9 + 7;
int n;
vector<int>G[N];
int dep[N], siz[N], fa[N], son[N];
void dfs1(int u, int _fa) {
siz[u] = 1; fa[u] = _fa;
for (int v : G[u]) {
if (v == _fa)continue;
dep[v] = dep[u] + 1;
dfs1(v, u);
siz[u] += siz[v];
if (siz[v] > siz[son[u]])son[u] = v;
}
}
int sn[N];
int main() {
scanf("%d", &n);
for (int i = 1; i < n; i++) {
int u, v;
scanf("%d%d", &u, &v);
G[u].push_back(v);
G[v].push_back(u);
}
dfs1(1, 0);
int u = 1, dx, dv, v, y, dis;
cout << "d " << 1 << endl;
cin >> dx;
while (1) {
y = u;
while (son[y]) {
sn[dep[y]] = y;
y = son[y];
}
sn[dep[y]] = y;
cout << "d " << y << endl;
cin >> dis;
dv = (dx + dep[y] - dis) / 2;
v = sn[dv];
if (dv == dx) {
cout << "! " << v << endl;
break;
}
cout << "s " << v << endl;
cin >> u;
}
return 0;
}
|







