http://codeforces.com/contest/1285
D. Dr. Evil Underscores
题意:给定一个数组,求出 X 使得 1≤i≤nmax(ai⊕X),要求输出结果。
对于二进制下某一位,如果既有1又有0,那么不管X取什么,最大值这一位一定为1.否则,一定为0。但是在为1的情况下又分X为0还是1,可能会导致不同的后续结果,所以要dfs搜下去,主要是要知道复杂度是够的,这就是一棵完全二叉树,一共最多n个叶子,logn 层,复杂度是 O(n) 的。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
| #include<bits/stdc++.h>
using namespace std;
#define ll long long
typedef pair<int, int> pii;
const int INF = 0x3f3f3f3f;
const int N = 1e5 + 10;
int n;
vector<int>vc;
int dfs(int dep, const vector<int>& vc) {
if (dep == -1)return 0;
vector<int>v[2];
for (int u : vc) {
if (u&(1 << dep))v[1].push_back(u);
else v[0].push_back(u);
}
if (v[0].empty())return dfs(dep - 1, v[1]);
else if (v[1].empty())return dfs(dep - 1, v[0]);
else {
return min(dfs(dep - 1, v[0]), dfs(dep - 1, v[1])) + (1 << dep);
}
}
int main() {
scanf("%d", &n);
for (int i = 0; i < n; i++) {
int x;
scanf("%d", &x);
vc.push_back(x);
}
printf("%d\n", dfs(30, vc));
return 0;
}
|
E. Delete a Segment
题意:给定几个区间,要求删除一个区间后并集的段数最多。
做法一:
参考 https://www.cnblogs.com/syksykCCC/p/CF1285E.html
前缀和
和普通的区间覆盖操作一样,用差分,前缀和维护最终结果,可以根据每个点与它右边点的值是否相等判断是否为段的边界。
但是存在以下情况:

所以要把坐标乘2
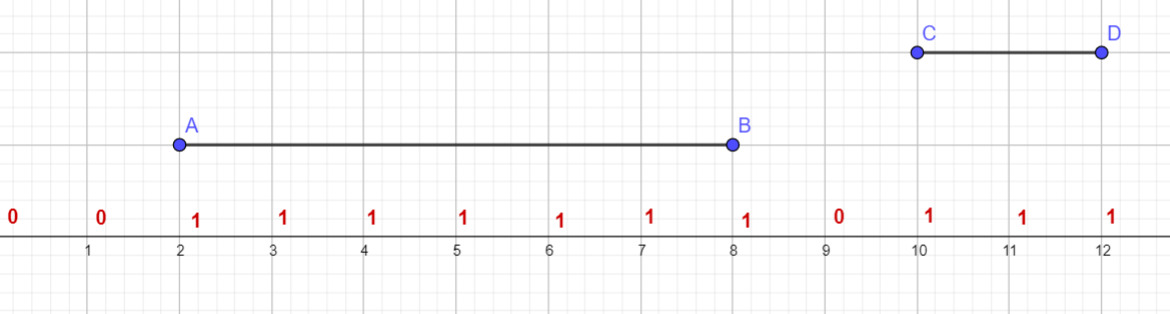
枚举每个区间,看删除后有几段,删除一个区间对它覆盖的点有影响。
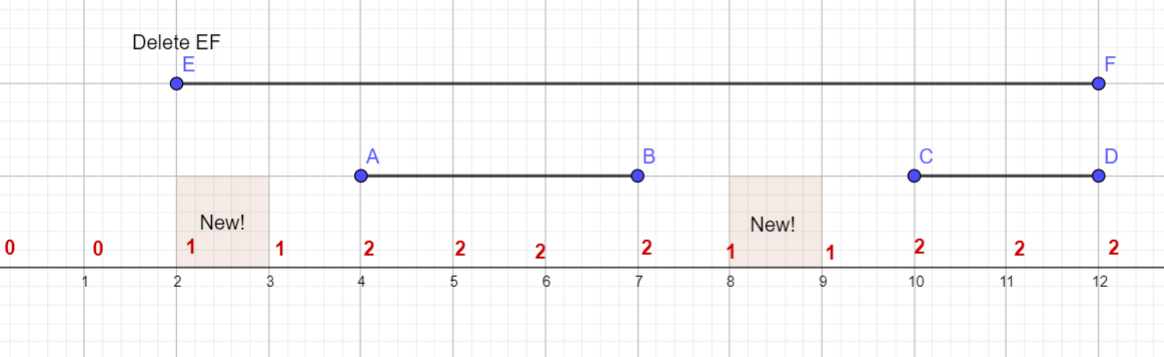
可以发现增加的段数为该区间下空白段数-两端的空白段数。
而区间下的空白段数就是值为1的段数,可以和刚开始判断段数一样,看当前点和右边点,判断是否为边界,再来一次前缀和维护区间里的为边界的点的个数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
| #include<bits/stdc++.h>
using namespace std;
#define ll long long
typedef pair<int, int> pii;
const int INF = 0x3f3f3f3f;
const int N = 2e5 + 10;
int T;
int n;
int l[N], r[N], tmp[N << 2];
int d[N << 2], d1[N << 2], ans0, ans1;
int main() {
cin >> T;
while (T--) {
scanf("%d", &n);
for (int i = 0; i < n; i++) {
scanf("%d%d", &l[i], &r[i]);
tmp[i << 1] = l[i];
tmp[i << 1 | 1] = r[i];
}
sort(tmp, tmp + 2 * n);
int tot = unique(tmp, tmp + 2 * n) - tmp;
for (int i = 0; i < n; i++) {
l[i] = ((lower_bound(tmp, tmp + tot, l[i]) - tmp) << 1) + 1;
r[i] = ((lower_bound(tmp, tmp + tot, r[i]) - tmp) << 1) + 1;
}
tot <<= 1;
fill(d, d + tot + 1, 0); fill(d1, d1 + tot + 1, 0);
ans0 = 0, ans1 = -INF;
for (int i = 0; i < n; i++)d[l[i]]++, d[r[i] + 1]--;
for (int i = 1; i <= tot; i++)d[i] += d[i - 1];
for (int i = 1; i <= tot; i++)if (d[i] && !d[i + 1])ans0++;
for (int i = 1; i <= tot; i++)if (d[i] == 1 && d[i + 1] != 1)d1[i]++;
for (int i = 1; i <= tot; i++)d1[i] += d1[i - 1];
for (int i = 0; i < n; i++)
ans1 = max(ans1, d1[r[i]] - d1[l[i] - 1] - (d[l[i]] == 1) - (d[r[i]] == 1));
printf("%d\n", ans0 + ans1);
}
return 0;
}
|
做法二:
单调栈
把区间按照左端点排序,再从大到小遍历,删除一个区间剩下的段数=它左边所有区间组成的段数+右边没有被左边覆盖的区间组成的段数。
用单调栈维护右边所有不相交的区间,每次二分查询没有被左边覆盖的区间个数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
| #include<bits/stdc++.h>
using namespace std;
#define ll long long
typedef pair<int, int> pii;
const int INF = 0x3f3f3f3f;
const int N = 2e5 + 10;
int T;
int n;
pii p[N];
int blo[N], r[N], S[N], top;
bool cmp(int a, int b) { return a > b; }
int main() {
cin >> T;
while (T--) {
scanf("%d", &n);
fill(blo, blo + n + 1, 0);
fill(r, r + n + 1, 0);
for (int i = 1; i <= n; i++)scanf("%d%d", &p[i].first, &p[i].second);
sort(p + 1, p + n + 1);
r[0] = -2e9;
for (int i = 1; i <= n; i++) {
blo[i] = blo[i - 1];
if (p[i].first > r[i - 1])blo[i]++;
r[i] = max(r[i - 1], p[i].second);
}
int ans = 0; top = 0;
for (int i = n; i >= 1; i--) {
int pos = lower_bound(S, S + top, r[i - 1], cmp) - S;
ans = max(ans, blo[i - 1] + pos);
while (top&&p[i].second >= S[top - 1])--top;
S[top++] = p[i].first;
}
printf("%d\n", ans);
}
return 0;
}
|









