https://codeforces.com/contest/1479

A. Searching Local Minimum

 

题意：交互题。有一个排列，最多 100 次询问，找到排列中的极小值。每次询问返回询问位置的值。

三分

三分必定能够找到一个极值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#include <bits/stdc++.h>
#define debug(x) cout << #x << ":\t" << (x) << endl;
using namespace std;
#define ll long long
#define ull unsigned ll
const int N = 2e6 + 5;
const int INF = 0x3f3f3f3f;
const ll inf = 0x3f3f3f3f3f3f3f3f;
const ll mod = 1e9 + 7;
const ll inv2 = (mod + 1) / 2;
int n;
int ask(int p) {
	if (p<1 || p>n)return INF;
	cout << "? " << p << endl;
	int x;
	cin >> x;
	return x;
}
int a[N];
int main() {
	cin >> n;
	int L = 1, R = n;
	while (R - L >= 3) {
		int m1 = (L + R) / 2, m2 = (m1 + R) / 2;
		if (ask(m1) > ask(m2))L = m1;
		else R = m2;
	}
	for (int i = L - 1; i <= R + 1; i++)a[i] = ask(i);
	for (int i = L; i <= R; i++) {
		if (a[i] < a[i - 1] && a[i] < a[i + 1]) {
			cout << "! " << i << endl;
			return 0;
		}
	}
	return 0;
}

 

B1. Painting the Array I

 

题意：给定一个序列，要拆成两个序列，且内部的相对顺序不变。定义一个序列的权值为序列删除相邻的相同元素后剩余元素个数。要求最大化拆成的两个序列的权值和。

可以发现重要的只有两个序列的最后一个元素。

初始答案为 n，遍历每个数，考虑如果当前数一定无法产生贡献，则答案-1.

遍历每个数，同时维护两个序列的最后一个数，若这两个都等于当前数，则一定无法产生贡献，否则把当前数放入任意一个不等于当前数的序列中。还需要判断如果这三个数两两不同，则可以替换任意一个，也就是说有一个任意牌，因此要把一个序列的末尾视为 0。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
#include <bits/stdc++.h>
#define debug(x) cout << #x << ":\t" << (x) << endl;
using namespace std;
#define ll long long
#define ull unsigned ll
const int N = 2e5 + 5;
const int INF = 0x3f3f3f3f;
const ll inf = 0x3f3f3f3f3f3f3f3f;
const ll mod = 1e9 + 7;
const ll inv2 = (mod + 1) / 2;
int n;
int a[N], c[2];
int main() {
	scanf("%d", &n);
	for (int i = 1; i <= n; i++)scanf("%d", &a[i]);
	int ans = n;
	for (int i = 1; i <= n; i++) {
		if (c[0] == a[i]) {
			if (c[1] == a[i])ans--;
			else c[1] = a[i];
		}
		else {
			if (c[1] == a[i]) {
				c[0] = a[i];
			}
			else {
				if (c[0] != c[1])c[0] = c[1] = 0;
				c[0] = a[i];
			}
		}
	}
	printf("%d\n", ans);
	return 0;
}

 

B2. Painting the Array II

 

题意：同上一题。要求最小化两个序列的权值和。

dp/贪心

我太弱了。自己做只会dp。

因为每次处理后必定有一个序列的某位等于当前数，所以只要维护另一个某位是几。dp[i]dp[i] 表示另一个末尾是 ii，特别地，dp[a[i]]dp[a[i]] 表示另一个序列为空。则分情况讨论转移即可，配合线段树区间加和查询最小值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
#include <bits/stdc++.h>
#define debug(x) cout << #x << ":\t" << (x) << endl;
using namespace std;
#define ll long long
#define ull unsigned ll
const int N = 2e5 + 5;
const int INF = 0x3f3f3f3f;
const ll inf = 0x3f3f3f3f3f3f3f3f;
const ll mod = 1e9 + 7;
const ll inv2 = (mod + 1) / 2;
int n;
int a[N], dp[N];
#define mid ((l+r)>>1)
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
int tr[N << 2], laz[N << 2];
void up(int rt) {
	tr[rt] = min(tr[rt << 1], tr[rt << 1 | 1]);
}
void build(int l, int r, int rt) {
	if (l == r) {
		tr[rt] = dp[l];
		return;
	}
	build(lson);
	build(rson);
	up(rt);
}
void down(int rt) {
	int& x = laz[rt];
	if (x) {
		tr[rt << 1] += x;
		tr[rt << 1 | 1] += x;
		laz[rt << 1] += x;
		laz[rt << 1 | 1] += x;
		x = 0;
	}
}
int qry(int ql, int qr, int l, int r, int rt) {
	if (ql > qr)return INF;
	if (ql <= l && qr >= r) {
		return tr[rt];
	}
	down(rt);
	int ans = INF;
	if (ql <= mid)ans = min(ans, qry(ql, qr, lson));
	if (qr > mid)ans = min(ans, qry(ql, qr, rson));
	return ans;
}
void add(int ql, int qr, int x, int l, int r, int rt) {
	if (ql > qr)return;
	if (ql <= l && qr >= r) {
		tr[rt] += x;
		laz[rt] += x;
		return;
	}
	if (ql <= mid)add(ql, qr, x, lson);
	if (qr > mid)add(ql, qr, x, rson);
	up(rt);
}
void cg(int q, int x, int l, int r, int rt) {
	if (q <= 0)return;
	if (l == r) {
		tr[rt] = x;
		return;
	}
	if (q <= mid)cg(q, x, lson);
	else cg(q, x, rson);
	up(rt);
}
int main() {
	scanf("%d", &n);
	for (int i = 1; i <= n; i++)scanf("%d", &a[i]);
	memset(dp, 0x3f, sizeof(dp));
	build(1, n, 1);
	int cnt = 1;
	cg(a[1], 1, 1, n, 1);
	for (int i = 2; i <= n; i++) {
		if (a[i] == a[i - 1])continue;
		cnt++;
		int x = min(qry(a[i], a[i], 1, n, 1), min(qry(1, a[i] - 1, 1, n, 1), qry(a[i] + 1, n, 1, n, 1)) + 1);
		cg(a[i - 1], x, 1, n, 1);
		cg(a[i], cnt, 1, n, 1);
		int l = min(a[i], a[i - 1]), r = max(a[i], a[i - 1]);
		add(1, l - 1, 1, 1, n, 1);
		add(l + 1, r - 1, 1, 1, n, 1);
		add(r + 1, n, 1, 1, n, 1);
	}
	int ans = cnt;
	for (int i = 1; i <= n; i++)ans = min(ans, qry(i, i, 1, n, 1));
	printf("%d\n", ans);
	return 0;
}

 

**贪心：**对操作系统或计组熟悉的话就能想到，这其实就是cache或者页表替换的问题。只有两个位置的cache，要最小化替换次数。在操作系统中我们学过：贪心地选择替换最远将要被使用的项。

也就是预处理出每个位置下一次与他值相同的位置，就是下一次要被使用的位置。

遍历每个数，如果cache中已经存在，则无事发生。否则找到两个cache中距离下次使用最远的那项替换掉，并答案+1.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
#include <bits/stdc++.h>
#define debug(x) cout << #x << ":\t" << (x) << endl;
using namespace std;
#define ll long long
#define ull unsigned ll
const int N = 2e5 + 5;
const int INF = 0x3f3f3f3f;
const ll inf = 0x3f3f3f3f3f3f3f3f;
const ll mod = 1e9 + 7;
const ll inv2 = (mod + 1) / 2;
int n;
int a[N], c[2], nxt[N], pos[N];
int main() {
	scanf("%d", &n);
	for (int i = 1; i <= n; i++)scanf("%d", &a[i]);
	int ans = 0;
	memset(nxt, 0x3f, sizeof(nxt));
	memset(pos, 0x3f, sizeof(pos));
	for (int i = n; i >= 1; i--) {
		nxt[i] = pos[a[i]];
		pos[a[i]] = i;
	}
	for (int i = 1; i <= n; i++) {
		if (a[c[0]] == a[i])c[0] = i;
		else if (a[c[1]] == a[i])c[1] = i;
		else {
			ans++;
			if (nxt[c[0]] > nxt[c[1]]) {
				c[0] = i;
			}
			else {
				c[1] = i;
			}
		}
	}
	printf("%d\n", ans);
	return 0;
}

 

C. Continuous City

 

题意：要求用不超过32个点构造出一张有向图，只能由编号小的向大的连边，没有重边。满足 1 到 n 的路径长度为 L 到 R 的连续区间。

二进制构造

首先考虑 L=1,R=2kL=1,R=2^k：

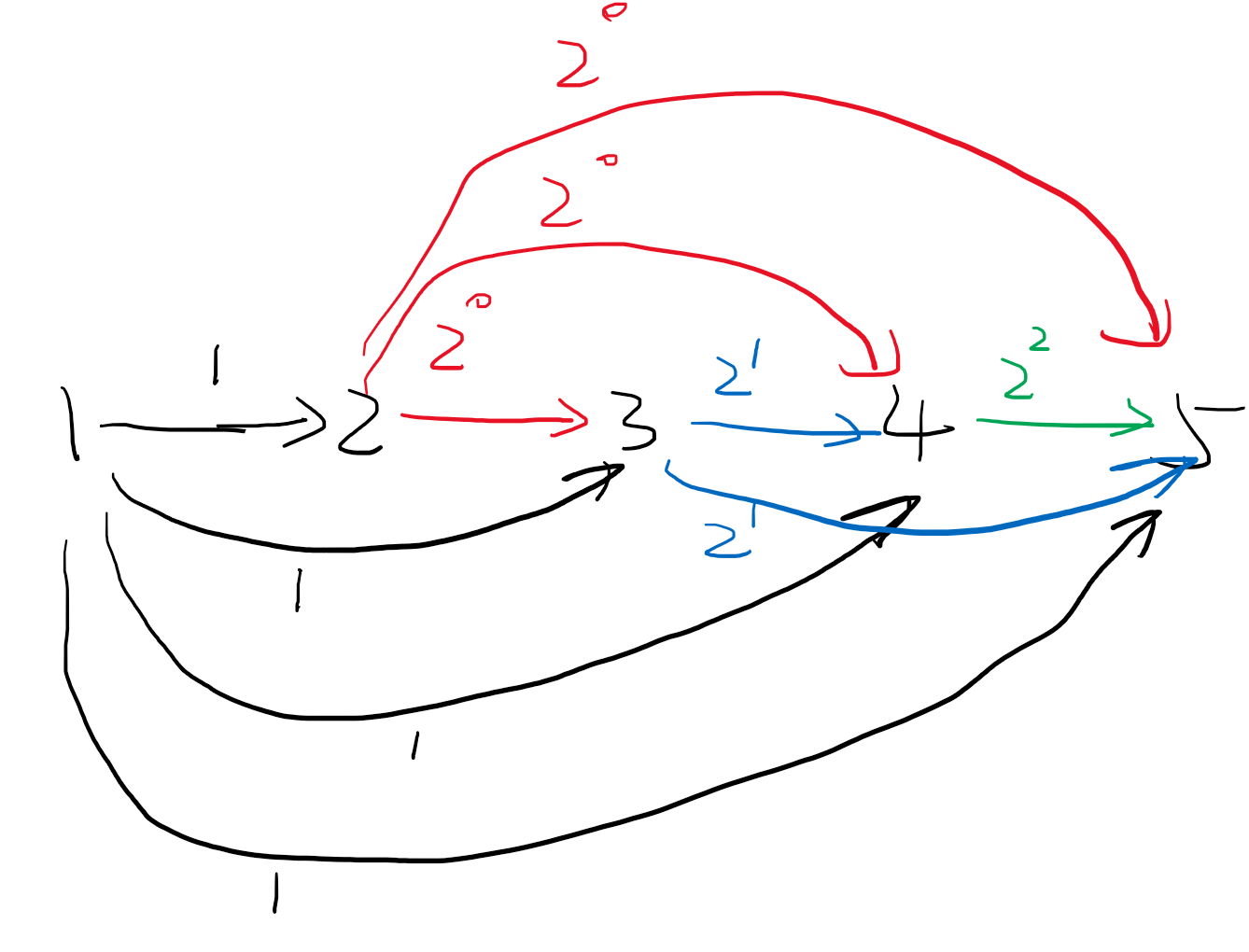
再考虑 L=1,R≠2kL=1,R\neq 2^{k}：记 R−1=∑i=0kpi2iR-1=\sum\limits_{i=0}^k p_i2^i，先用上面的方法构造出 (1,2k)−continuous(1,2^k)-continuous，则此时图上共有 k+2k+2 个点，再加入一个点 k+3k+3，先从 11 连向 k+3k+3，边权为 11，再对于每个点 2≤i≤k+22\le i\le k+2，若 pi−2=1p_{i-2}=1，即二进制下该位上是 11，则由于 11 到 ii 的路径长度可以取到 [1,2i−2][1,2^{i-2}]，所以直接从 ii 连向 k+3k+3，边权为 ∑j=i−1kpi2i+1\sum\limits_{j=i-1}^k p_i2^i + 1，相当于固定了最高的 k−i+2k-i+2 位，剩下的几位可以取遍。

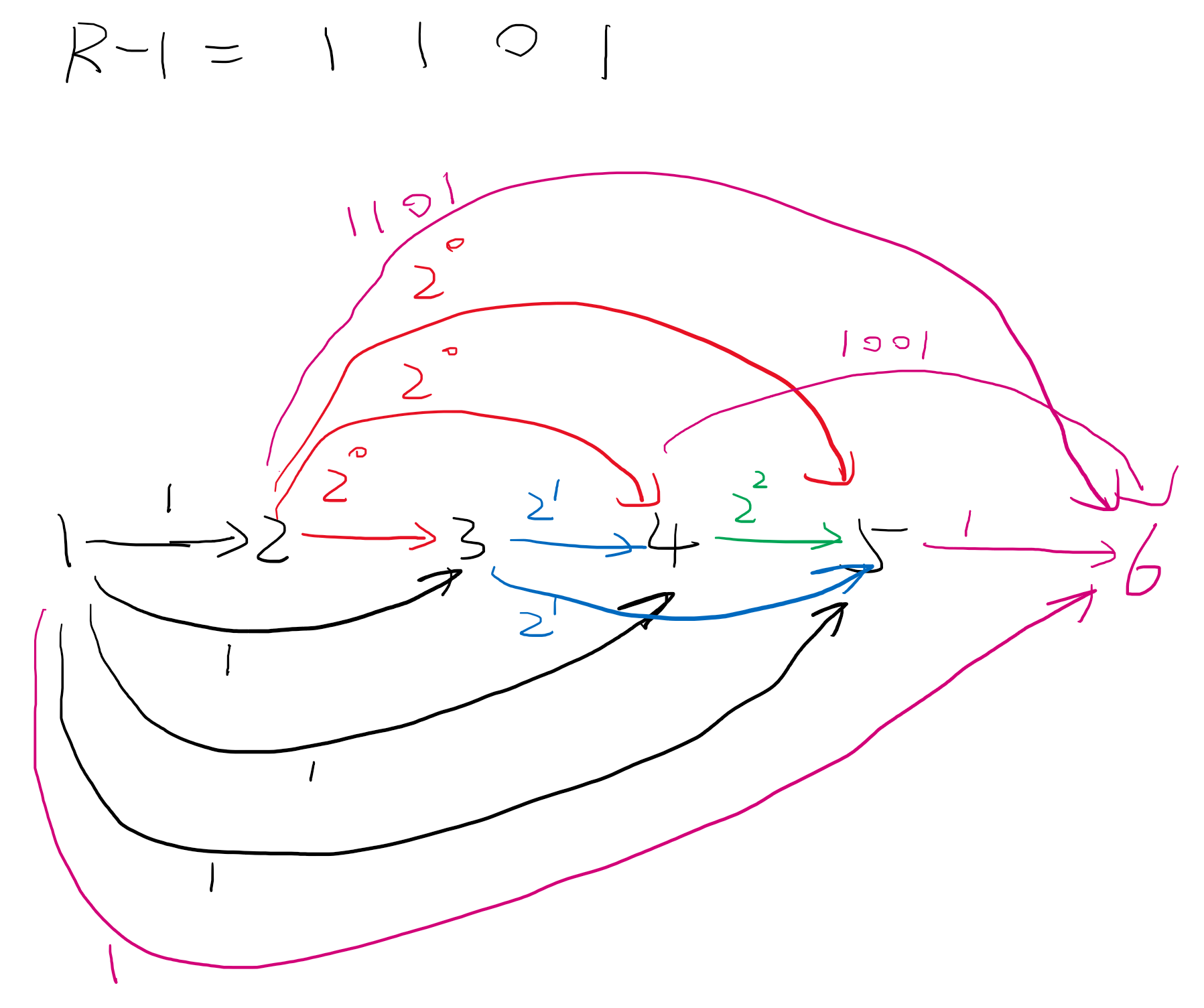
要注意这里是分解 R−1R-1，在最后加边时再把 11 加回来。因为范围是从 11 开始，所以 11 号点是特殊的，它连向其它所有点，边权都是 11，且 (1,2k)−continuous(1,2^k)-continuous 是 [1,2k][1,2^k] 而不是 [0,2k−1][0,2^k-1]。

最后考虑 L≠1L\neq 1：再加一个点 nn，从 n−1n-1 连向 nn，边权为 L−1L-1。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
#include <bits/stdc++.h>
#define debug(x) cout << #x << ":\t" << (x) << endl;
using namespace std;
#define ll long long
#define ull unsigned ll
const int N = 2e5 + 5;
const int INF = 0x3f3f3f3f;
const ll inf = 0x3f3f3f3f3f3f3f3f;
const ll mod = 1e9 + 7;
const ll inv2 = (mod + 1) / 2;
int L, R;
struct E
{
	int u, v, w;
};
vector<E>ans;
int main() {
	scanf("%d%d", &L, &R);
	int x = L - 1;
	L -= x; R -= x;
	puts("YES");
	int tmp = R, k = -1;
	while (tmp) {
		tmp >>= 1;
		k++;
	}
	for (int i = 2; i <= k + 2; i++)ans.push_back({ 1,i,1 });
	for (int i = 2; i < k + 2; i++) {
		for (int j = i + 1; j <= k + 2; j++) {
			ans.push_back({ i,j,1 << (i - 2) });
		}
	}
	int n = k + 2;
	if (R ^ (1 << k)) {
		R--;
		n++;
		tmp = R;
		ans.push_back({ 1,n,1 });
		for (int i = 2; i <= k + 2; i++) {
			if (tmp >> (i - 2) & 1) {
				tmp ^= (1 << (i - 2));
				if (tmp + 1)ans.push_back({ i,n,tmp + 1 });
			}
		}
	}
	if (x) {
		n++;
		ans.push_back({ n - 1,n,x });
	}
	printf("%d %d\n", n, (int)ans.size());
	for (E e : ans) {
		printf("%d %d %d\n", e.u, e.v, e.w);
	}
	return 0;
}

 

D. Odd Mineral Resource

 

题意：给定一棵树，有点权，多次询问，每次问 u,vu,v 两点之间是否有 [l,r][l,r] 之间的权值出现奇数次，有则输出任意一个。

两种做法：树上莫队+分块 / 哈希+树上差分+可持久化线段树

做法一：树上莫队+分块

对于多个区间且每次转移到相邻区间复杂度 O(1)O(1) 的询问可以进行离线后莫队。而本题这种树上的两点间的询问就是树上莫队了。

树上莫队的思想就是把树变成欧拉序后问题转化为区间上的普通莫队。

而莫队则是分块的思想，左端点以块号排序，右端点作为第二关键字排序。

转化为欧拉序后，若 uu 是 vv 的 lcalca，则查询的区间为 [in[u],in[v]][in[u],in[v]]，否则查询区间为 [out[u],in[v]][out[u],in[v]]，反过来也一样。区间中若既有 in[x]in[x] 又有 out[x]out[x]，则说明 xx 不在路径上。

又由于点权的范围又是区间，所以还需要再来一个分块，对点权分块，每次 O(1)O(1) 修改，O(n)O(\sqrt{n}) 查询。

这样复杂度就是根号的，常数很大。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
#include <bits/stdc++.h>
#define debug(x) cout << #x << ":\t" << (x) << endl;
using namespace std;
#define ll long long
#define ull unsigned ll
const int N = 2e6 + 5;
const int INF = 0x3f3f3f3f;
const ll inf = 0x3f3f3f3f3f3f3f3f;
const ll mod = 1e9 + 7;
const ll inv2 = (mod + 1) / 2;
int n, q;
int a[N];
vector<int>G[N];
const int S = 500;
int ans[N];
struct Q
{
	int lca, tl, tr, L, R, id;
	bool operator<(const Q& b)const {
		return tl / S == b.tl / S ? tr < b.tr : tl / S < b.tl / S;
	}
}qq[N];
int clk, in[N], out[N], siz[N], fa[N], dep[N], son[N], topf[N], b[N];
void dfs1(int u, int _fa) {
	siz[u] = 1; fa[u] = _fa;
	in[u] = ++clk;
	b[clk] = u;
	for (int v : G[u]) {
		if (v == _fa)continue;
		dep[v] = dep[u] + 1;
		dfs1(v, u);
		siz[u] += siz[v];
		if (siz[v] > siz[son[u]])son[u] = v;
	}
	out[u] = ++clk;
	b[clk] = u;
}
void dfs2(int u, int topfa) {
	topf[u] = topfa;
	if (!son[u])return;
	dfs2(son[u], topfa);
	for (int v : G[u]) {
		if (!topf[v])dfs2(v, v);
	}
}
int LCA(int u, int v) {
	while (topf[u] ^ topf[v]) {
		dep[topf[u]] < dep[topf[v]] ? v = fa[topf[v]] : u = fa[topf[u]];
	}
	return dep[u] < dep[v] ? u : v;
}
int flg[N], cnt[N];
void add(int x) {
	if (!x)return;
	if (flg[x]) {
		cnt[x / S]--;
	}
	else {
		cnt[x / S]++;
	}
	flg[x] ^= 1;
}
int cal(int l, int r) {
	int bl = l / S, br = r / S;
	for (int i = l; i <= min(r, (bl + 1)*S - 1); i++) {
		if (flg[i])return i;
	}
	for (int i = bl + 1; i < br; i++) {
		if (cnt[i]) {
			for (int j = i * S; j < (i + 1)*S; j++) {
				if (flg[j])return j;
			}
		}
	}
	for (int i = max(l, br * S); i <= r; i++) {
		if (flg[i])return i;
	}
	return -1;
}
int main() {
	scanf("%d%d", &n, &q);
	for (int i = 1; i <= n; i++)scanf("%d", &a[i]);
	for (int i = 1; i < n; i++) {
		int u, v;
		scanf("%d%d", &u, &v);
		G[u].push_back(v);
		G[v].push_back(u);
	}
	dfs1(1, 0);
	dfs2(1, 1);
	for (int i = 1; i <= q; i++) {
		int u, v, l, r;
		scanf("%d%d%d%d", &u, &v, &l, &r);
		int lca = LCA(u, v);
		if (lca == u) {
			qq[i] = { 0,in[u],in[v],l,r,i };
		}
		else if (lca == v) {
			qq[i] = { 0,in[v],in[u],l,r,i };
		}
		else if (out[u] < in[v]) {
			qq[i] = { lca,out[u],in[v],l,r,i };
		}
		else {
			qq[i] = { lca,out[v],in[u],l,r,i };
		}
	}
	sort(qq + 1, qq + q + 1);
	int L = 1, R = 0;
	for (int i = 1; i <= q; i++) {
		int curl = qq[i].tl, curr = qq[i].tr;
		while (L < curl) {
			add(a[b[L++]]);
		}
		while (L > curl) {
			add(a[b[--L]]);
		}
		while (R < curr) {
			add(a[b[++R]]);
		}
		while (R > curr) {
			add(a[b[R--]]);
		}
		int lca = qq[i].lca;
		if (lca)add(a[lca]);
		ans[qq[i].id] = cal(qq[i].L, qq[i].R);
		if (lca)add(a[lca]);
	}
	for (int i = 1; i <= q; i++) {
		printf("%d\n", ans[i]);
	}
	return 0;
}

 

做法二：哈希+树上差分+可持久化线段树

对每一个点权值进行哈希，保证异或值为 00 等价于两个值相同。

这样只要判断一个点权值区间 [l,r][l,r] 的异或值是否为 00 就能知道是否存在出现奇数次的点权值。

再根据树上差分和主席树的思想，得到两点之间的点权值区间 [l,r][l,r] 的异或值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
#include <bits/stdc++.h>
#define debug(x) cout << #x << ":\t" << (x) << endl;
using namespace std;
#define ll long long
#define ull unsigned ll
const int N = 3e5 + 5;
const int INF = 0x3f3f3f3f;
const ll inf = 0x3f3f3f3f3f3f3f3f;
const ll mod = 1e9 + 7;
const ll inv2 = (mod + 1) / 2;
mt19937_64 mt(chrono::steady_clock::now().time_since_epoch().count());
int n, q;
int a[N];
vector<int>G[N];
ll hsh[N];
#define mid ((l+r)>>1)
struct X
{
	int lc, rc; ll xsum;
}T[N << 5];
int tot, root[N];
void upd(int l, int r, int& x, int y, int q) {
	T[++tot] = T[y];
	T[tot].xsum ^= hsh[q];
	x = tot;
	if (l == r)return;
	if (q <= mid)upd(l, mid, T[x].lc, T[y].lc, q);
	else upd(mid + 1, r, T[x].rc, T[y].rc, q);
}
int siz[N], fa[N], dep[N], son[N], topf[N];
void dfs1(int u, int _fa) {
	siz[u] = 1; fa[u] = _fa;
	upd(1, n, root[u], root[_fa], a[u]);
	for (int v : G[u]) {
		if (v == _fa)continue;
		dep[v] = dep[u] + 1;
		dfs1(v, u);
		siz[u] += siz[v];
		if (siz[v] > siz[son[u]])son[u] = v;
	}
}
void dfs2(int u, int topfa) {
	topf[u] = topfa;
	if (!son[u])return;
	dfs2(son[u], topfa);
	for (int v : G[u]) {
		if (!topf[v])dfs2(v, v);
	}
}
int LCA(int u, int v) {
	while (topf[u] ^ topf[v])
		dep[topf[u]] < dep[topf[v]] ? v = fa[topf[v]] : u = fa[topf[u]];
	return dep[u] < dep[v] ? u : v;
}
int qry(int u, int v, int lca, int flc, int ql, int qr, int l, int r) {
	ll xs = T[u].xsum^T[v].xsum^T[lca].xsum^T[flc].xsum;
	if (xs == 0)return -1;
	if (l == r)return l;
	int ans = -1;
	if (ql <= mid)ans = qry(T[u].lc, T[v].lc, T[lca].lc, T[flc].lc, ql, qr, l, mid);
	if (ans == -1 && qr > mid)ans = qry(T[u].rc, T[v].rc, T[lca].rc, T[flc].rc, ql, qr, mid + 1, r);
	return ans;
}
int main() {
	srand(time(0));
	scanf("%d%d", &n, &q);
	for (int i = 1; i <= n; i++)scanf("%d", &a[i]);
	for (int i = 1; i < n; i++) {
		int u, v;
		scanf("%d%d", &u, &v);
		G[u].push_back(v);
		G[v].push_back(u);
	}
	for (int i = 1; i <= n; i++) {
		hsh[i] = mt();
	}
	dfs1(1, 0);
	dfs2(1, 1);
	while (q--) {
		int u, v, l, r;
		scanf("%d%d%d%d", &u, &v, &l, &r);
		int lca = LCA(u, v);
		printf("%d\n", qry(root[u], root[v], root[lca], root[fa[lca]], l, r, 1, n));
	}
	return 0;
}