http://codeforces.com/contest/1498
D. Bananas in a Microwave
题意:你有一个数 k,初始为 0,给定 n 轮操作,每轮操作给定 t,x,y,若 t=1,则可以向你手中的数进行不超过 y 次 k:=⌈(k+xi)⌉;若 t=2,则可以向你手中的数进行不超过 y 次 k:=⌈(k⋅xi)⌉。给定 m,问对于 1≤i≤m,最少几轮操作后可以得到 i。
滑动窗口+dp
dp[i][j]=0/1 表示第 i 轮,不能/能 凑出 j。
第一种操作比较简单,由于每次加完后都要上取整,所以相当于先把 xi 上取整,之后就直接 $k:=k + x_i $。
则有 dp[i][j]=∣k=j−p∗x∧p≤ydp[i][k],也就是 k 与 j 模 x 同余,则对于每个余数维护窗口内的 dp=1 的个数。
第二种操作的思路相同,但是由于是乘法,无法去掉取整符号。
若 v=⌈(u⋅xi)⌉,则从 u 向 v 连边,预处理所有数字建图,得到若干条链,记录链首和每点在链上的深度,则变成一个链上的滑动窗口,窗口的长度就是两点的深度dep值之差。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
| #include <bits/stdc++.h>
#define debug(x) cout << #x << ":\t" << (x) << endl;
using namespace std;
#define ll long long
#define ull unsigned ll
const int N = 2e6 + 10;
const int INF = 0x3f3f3f3f;
const ll inf = 0x3f3f3f3f3f3f3f3f;
const ll mod = 1e9 + 7;
const ll inv2 = (mod + 1) / 2;
int n, m;
int dp[210][100010], c[N], st[N], dep[N];
int main() {
scanf("%d%d", &n, &m);
dp[0][0] = 1;
for (int i = 1; i <= n; i++) {
int op;
ll x, y;
scanf("%d%lld%lld", &op, &x, &y);
for (int j = 0; j <= m; j++)dp[i][j] = dp[i - 1][j];
fill(c, c + m + 1, 0);
if (op == 1) {
c[0] = 1;
x = (x + 100000 - 1) / 100000;
for (int j = 1; j <= m; j++) {
if (j - x * (y + 1) >= 0)c[j%x] -= dp[i - 1][j - x * (y + 1)];
if (c[j%x] > 0)dp[i][j] = 1;
c[j%x] += dp[i - 1][j];
}
}
else {
fill(dep, dep + m + 1, 0);
fill(st, st + m + 1, 0);
for (int i = 1; i < (x + 100000 - 1) / 100000; i++) {
st[i] = i;
}
for (int i = 1; i <= m; i++) {
if (!st[i])st[i] = i, dep[i] = 0;
ll nx = (ll)ceil(i*1.0*x / 100000);
if (nx <= m)st[nx] = st[i], dep[nx] = dep[i] + 1;
else break;
}
int L = 1;
for (int j = 1; j <= m; j++) {
if (!st[j])continue;
while (st[L] == st[j] && dep[j] - dep[L] > y) {
c[st[L]] -= dp[i - 1][L];
L++;
}
if (c[st[j]] > 0)dp[i][j] = 1;
c[st[j]] += dp[i - 1][j];
}
}
}
for (int i = 1; i <= m; i++) {
int ans = -1;
for (int j = 1; j <= n; j++) {
if (dp[j][i]) {
ans = j;
break;
}
}
printf("%d%c", ans, " \n"[i == m]);
}
return 0;
}
|
E. Two Houses
题意:交互题。有一张有向图,每对点之间有且仅有一条边但不知道方向,给出了每个点的入度,可以进行任意次数询问,每次询问返回 u 是否可达 v,要求在第一次返回Yes,或询问完所有点对后,给出两个点满足互相可达,且入度之差最大。
贪心
考虑极端情况,第一次询问 (u,v) 就返回Yes,那么必须要 (v,u) 可达,所以考虑两点可达的充分条件。
若 u 的出度与 v 的入度之和大于等于 n−1,则 u 一定可达 v。
证明:假设不存在点 w 满足存在边 u−>w 与 w−>v,则每个点对于 out[u]+in[v] 最多贡献 1,那么 out[u]+in[v] 最大只会是 n−2。所以假设不成立。
又由于每一对点都有边,所以 in[u]+out[u]=n−1,所以 out[u]+in[v]≥n−1 化为 in[u]≤in[v]。
也就是说,对于一对点 (u,v),只要询问时满足 in[u]>in[v],则只要返回Yes,就是双向可达,只要返回No,一定不是双向可达(因为询问的这个方向已经不可达了)。
所以把所有点对按照入度差从大到小排序,贪心询问即可。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
| #include <bits/stdc++.h>
#define debug(x) cout << #x << ":\t" << (x) << endl;
using namespace std;
#define ll long long
#define ull unsigned ll
const int N = 2e6 + 10;
const int INF = 0x3f3f3f3f;
const ll inf = 0x3f3f3f3f3f3f3f3f;
const ll mod = 1e9 + 7;
const ll inv2 = (mod + 1) / 2;
int n;
int a[N];
struct X
{
int u, v, d;
bool operator<(const X& b)const {
return d > b.d;
}
};
vector<X>vc;
char s[N];
int main() {
cin >> n;
for (int i = 1; i <= n; i++)cin >> a[i];
for (int i = 1; i <= n; i++) {
for (int j = i + 1; j <= n; j++) {
if (a[i] > a[j])vc.push_back({ i,j,a[i] - a[j] });
else vc.push_back({ j,i,a[j] - a[i] });
}
}
sort(vc.begin(), vc.end());
for (X& p : vc) {
cout << "? " << p.u << ' ' << p.v << endl;
cin >> s;
if (s[0] == 'Y') {
cout << "! " << p.u << ' ' << p.v << endl;
return 0;
}
}
cout << "! 0 0" << endl;
return 0;
}
|
F. Christmas Game
题意:给定一棵树,树上每个节点有些石子,两人轮流操作,每次操作选择一个深度大于等于 k 的节点,把一些石子移动到它第 k 个祖先上,不能操作的人输,问以每个点作为树根的情况下,先手输赢。
阶梯Nim+树上dp+换根dp
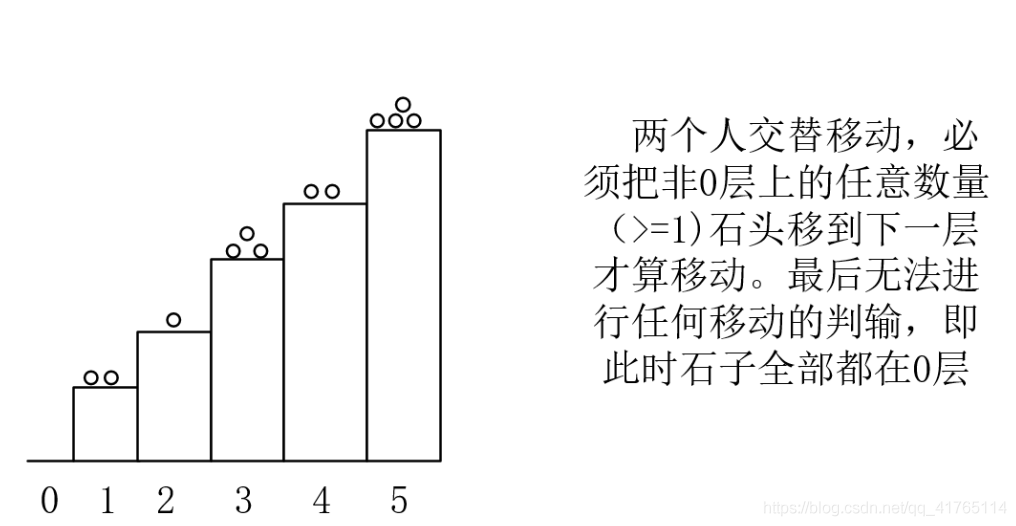
本题就是每个台阶梯深度为 k 的树上的阶梯尼姆游戏。阶梯尼姆游戏判断奇数台阶上的异或和,若不为零则先手胜,否则后手胜。
所以现在问题在于快速求出每个根的情况下奇数阶梯上的节点的异或和。
dp[u][i] 表示节点 u 的子树中与 u 的距离模 2k 等于 i 的节点的异或和。之所以取模 2k 是因为这样可以区分奇偶台阶,若模 k 则不同台阶h同余的位置会混在一起。
树上dp由儿子 v 转移到父亲 u
dp[u][dep]dp[u][0]=v⨁dp[v][dep−1]=dp[v][2∗k−1]
上面的dp只是对于 u 的子树中的,再维护对全局的,tmp[u][i] 表示在整棵树上与 u 的距离模 2k 等于 i 的节点的异或和。
再来一个换根dp,与第一个dp的思路类似,但是需要先从上一个根的结果中去掉新根的子树,再深度循环平移一格,再加入新根的子树。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
| #include <bits/stdc++.h>
#define debug(x) cout << #x << ":\t" << (x) << endl;
using namespace std;
#define ll long long
#define ull unsigned ll
const int N = 2e5 + 10;
const int INF = 0x3f3f3f3f;
const ll inf = 0x3f3f3f3f3f3f3f3f;
const ll mod = 1e9 + 7;
const ll inv2 = (mod + 1) / 2;
int n, k;
vector<int>G[N];
int a[N];
int dp[N][50];
void dfs(int u, int _fa) {
dp[u][0] = a[u];
for (int v : G[u]) {
if (v == _fa)continue;
dfs(v, u);
for (int i = 1; i < 2 * k; i++) {
dp[u][i] ^= dp[v][i - 1];
}
dp[u][0] ^= dp[v][2 * k - 1];
}
}
int ans[N], tmp[N][50];
void dfs2(int u, int _fa) {
if (u == 1) {
for (int i = 0; i < 2 * k; i++)tmp[u][i] = dp[u][i];
}
else {
for (int i = 0; i < 2 * k; i++)tmp[u][i] = tmp[_fa][i];
for (int i = 1; i < 2 * k; i++) {
tmp[u][i] ^= dp[u][i - 1];
}
tmp[u][0] ^= dp[u][2 * k - 1];
int t = tmp[u][2 * k - 1];
for (int i = 2 * k - 1; i >= 1; i--) {
tmp[u][i] = tmp[u][i - 1];
}
tmp[u][0] = t;
for (int i = 0; i < 2 * k; i++) {
tmp[u][i] ^= dp[u][i];
}
}
for (int i = k; i < 2 * k; i++) {
ans[u] ^= tmp[u][i];
}
for (int v : G[u]) {
if (v == _fa)continue;
dfs2(v, u);
}
}
int main() {
scanf("%d%d", &n, &k);
for (int i = 1; i < n; i++) {
int u, v;
scanf("%d%d", &u, &v);
G[u].push_back(v);
G[v].push_back(u);
}
for (int i = 1; i <= n; i++)scanf("%d", &a[i]);
dfs(1, 0);
dfs2(1, 0);
for (int i = 1; i <= n; i++)printf("%d%c", ans[i] != 0, " \n"[i == n]);
return 0;
}
|







