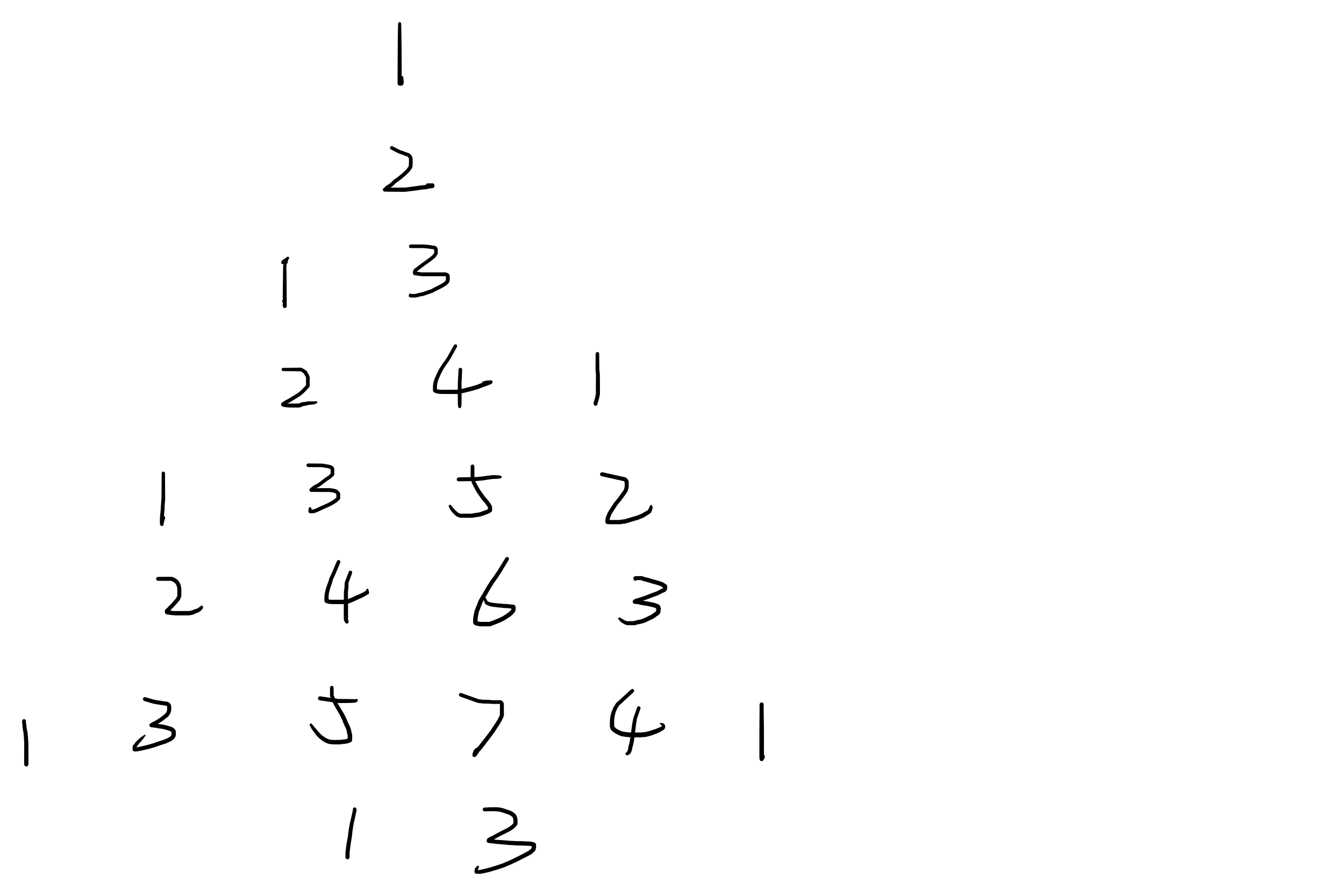http://acm.hdu.edu.cn/contests/contest_show.php?cid=882

1007 - Go Running

 

题意：每个人可以选择任意的时间开始，任意时间结束，从任意位置出发，向左或右跑步，给出了 n 个报告，每次告诉你在第 t[i]t[i] 秒时坐标 x[i]x[i] 处至少有一个人。问最少有几个人跑过步了。

最小点覆盖/二分图匹配

如果 x[i]−t[i]=x[j]−t[j]x[i]-t[i]=x[j]-t[j] 则 i，j 可以视为同一个人向右跑。

如果 x[i]+t[i]=x[j]+t[j]x[i]+t[i]=x[j]+t[j] 则 i，j 可以视为同一个人向左跑。

所以问题变为平面上 n 个点 (xi,ti)(x_i,t_i)，要用最少的斜率为正负 1 的直线穿过所有点。

本来也想过网络流，但是想着网络流复杂度太大了，但是其实 Dinic 在二分图上的复杂度是 O(mn)O(m\sqrt n) 的。

每个点可以被两条直线选中，所以考虑把每个点变为 新图上两个点集的连边 x[i]−t[i]x[i]-t[i] 连向 x[i]+t[i]x[i]+t[i]。

这样每点可以被两种选择选中，所以拆成两个点集，把点变成边，再求最小点覆盖的模型在紫书和挑战程序设计上都有，也算是比较常用了，需要记住。

再求最小点覆盖，这样就能保证新图上所有边都被选中，也就是原图上所有点都被选中了。

二分图的最小点覆盖等于最大匹配，所以就是求最大匹配。

Dinic 求二分图最大匹配的复杂度是 O(mn)O(m\sqrt n)，在这里是完全够用的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int INF = 0x3f3f3f3f;
const ll inf = 0x3f3f3f3f3f3f3f3f;
const int N = 2e5 + 10;
const ll mod = 1e9 + 7;
const double eps = 1e-5;
struct mxfl
{
	int n = 0;
	int m = 0;
	int s, t;
	struct Edge
	{
		int from, to, cap, flow;
	};
	vector<Edge>edges;
	vector<int>G[N];
	void init(int _n, int _s, int _t) {
		n = _n;
		s = _s;
		t = _t;
		edges.clear();
		for (int i = 0; i < n; i++)G[i].clear();
	}
	void add_edge(int from, int to, int cap) {
		edges.push_back(Edge{ from,to,cap,0 });
		edges.push_back(Edge{ to,from,0,0 });
		m = (int)edges.size();
		G[from].push_back(m - 2);
		G[to].push_back(m - 1);
	}
	bool vis[N];
	int d[N], cur[N];
	bool bfs() {
		memset(vis, 0, sizeof(vis));
		queue<int>Q;
		Q.push(s);
		d[s] = 0;
		vis[s] = 1;
		while (!Q.empty()) {
			int x = Q.front(); Q.pop();
			for (int i = 0; i < (int)G[x].size(); i++) {
				Edge& e = edges[G[x][i]];
				if (!vis[e.to] && e.cap > e.flow) {
					vis[e.to] = 1;
					d[e.to] = d[x] + 1;
					Q.push(e.to);
				}
			}
		}
		return vis[t];
	}
	int dfs(int x, int a) {
		if (x == t || a == 0)return a;
		int flow = 0, f;
		for (int& i = cur[x]; i < (int)G[x].size(); i++) {
			Edge& e = edges[G[x][i]];
			if (d[x] + 1 == d[e.to] && (f = dfs(e.to, min(a, e.cap - e.flow))) > 0) {
				e.flow += f;
				edges[G[x][i] ^ 1].flow -= f;
				flow += f;
				a -= f;
				if (a == 0)break;
			}
		}
		return flow;
	}
	int maxflow() {
		int flow = 0;
		while (bfs()) {
			memset(cur, 0, sizeof(cur));
			flow += dfs(s, INF);
		}
		return flow;
	}
}MF;
int T;
int n;
int t[N], x[N];
vector<int>vc[2];
int main() {
	scanf("%d", &T);
	while (T--) {
		scanf("%d", &n);
		vc[0].clear();
		vc[1].clear();
		for (int i = 1; i <= n; i++) {
			scanf("%d%d", &t[i], &x[i]);
			vc[0].push_back(x[i] - t[i]);
			vc[1].push_back(x[i] + t[i]);
		}
		sort(vc[0].begin(), vc[0].end());
		sort(vc[1].begin(), vc[1].end());
		vc[0].erase(unique(vc[0].begin(), vc[0].end()), vc[0].end());
		vc[1].erase(unique(vc[1].begin(), vc[1].end()), vc[1].end());
		int S = 0, T = (int)vc[0].size() + (int)vc[1].size() + 1;
		MF.init(T + 1, S, T);
		for (int i = 1; i <= (int)vc[0].size(); i++)MF.add_edge(S, i, 1);
		for (int i = 1; i <= (int)vc[1].size(); i++)MF.add_edge((int)vc[0].size() + i, T, 1);
		for (int i = 1; i <= n; i++) {
			int a = lower_bound(vc[0].begin(), vc[0].end(), x[i] - t[i]) - vc[0].begin() + 1;
			int b = lower_bound(vc[1].begin(), vc[1].end(), x[i] + t[i]) - vc[1].begin() + 1 + (int)vc[0].size();
			MF.add_edge(a, b, 1);
		}
		printf("%d\n", MF.maxflow());
	}
	return 0;
}

 

1012 - Last Problem

 

题意：在一个二维坐标系的整点上写数字，要写一个数字 t 必须满足写下的这个数字四周已经写好了 t-1，t-2，t-3，t-4，非正数可以不管。要求写出数字 n。给出操作步骤。

构造

n=7

玩过2048的应该都清楚越大的数字要构造出需要的操作数是远大于小数的，所以肯定是习惯性地利用之前已经构造出的大数来构造出更大的，而不是从头开始。

所以也就可以尝试出上图中间一列，最终的 n 也就会出现在这一列。

接着就是各种尝试，目的就是要找出一种 “对称” 的构造方式。

如上图，要写下一个数字 t，需要按照 上，左，右，下 的顺序写下 t-1，t-2，t-3，t-4。

要从一开始就找到这个规律肯定是很难的，但是最开始可能会发现每一列都是 1，2，3 这样递增，那么就不断向着这个方向尝试，直到能找出可以递归的规律。

数据很小，其实只要能构造出来，必定不会超过限制。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int INF = 0x3f3f3f3f;
const ll inf = 0x3f3f3f3f3f3f3f3f;
const int N = 2e6 + 10;
const ll mod = 1e9 + 7;
int n;
int a[3000][3000];
void dfs(int x, int y, int num) {
	if (a[x][y] == num || num <= 0)return;
	dfs(x, y + 1, num - 1);
	dfs(x - 1, y, num - 2);
	dfs(x + 1, y, num - 3);
	dfs(x, y - 1, num - 4);
	printf("%d %d %d\n", x, y, num);
	a[x][y] = num;
}
int main() {
	scanf("%d", &n);
	for (int i = 1; i <= n; i++) {
		dfs(1000, 1000 - i + 1, i);
	}
	return 0;
}

 

1003 - Contest of Rope Pulling

 

题意：两个班级分别有 n，m 个人，每人有 w，v 两种属性，要求每班各选一些人，且两班的 w 的和相同，v 的和最大。

随机+dp

把第二个班级的人 w 取负，就相当于在 n+m 个人中选一个子集，w 和为 0，v 和最大。

这是很典型的01背包。复杂度应该是 值域*（n+m），复杂度太大。

但是其实并不需要取整个值域，因为最终我们需要的是 dp[n+m][0]dp[n+m][0]。所以要考虑定一个范围，范围外的直接忽略。

把整个集合随机打乱，再限定边界MX，对于 w 和超过MX的情况直接忽略。然后就是01背包。

这必然会有可能取不到正解，但是几率是非常小的。

至于证明还是看题解吧。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int INF = 0x3f3f3f3f;
const ll inf = 0x3f3f3f3f3f3f3f3f;
const int N = 2e6 + 10;
const ll mod = 1e9 + 7;
mt19937_64 mt(chrono::steady_clock::now().time_since_epoch().count());
int T;
int n, m;
typedef pair<int, ll>pii;
pii a[N];
ll dp[N], tmp[N];
int base = 100000, MX = 50000;
int main() {
	scanf("%d", &T);
	while (T--) {
		scanf("%d%d", &n, &m);
		for (int i = 1; i <= n; i++)scanf("%d%lld", &a[i].first, &a[i].second);
		for (int i = 1; i <= m; i++)scanf("%d%lld", &a[i + n].first, &a[i + n].second), a[i + n].first *= -1;
		shuffle(a + 1, a + n + m + 1, mt);
		n += m;
		for (int j = base - MX; j <= base + MX; j++)dp[j] = -inf;
		dp[base] = 0;
		for (int i = 1; i <= n; i++) {
			for (int j = -MX; j <= MX; j++)tmp[base + j] = dp[base + j];
			for (int j = max(-MX, -MX + a[i].first); j <= min(MX, MX + a[i].first); j++) {
				dp[base + j] = max(tmp[base + j], tmp[base + j - a[i].first] + a[i].second);
			}
		}
		printf("%lld\n", dp[base]);
	}
	return 0;
}