https://acm.ecnu.edu.cn/contest/361/
E. 护花行动
题意:给定一个矩阵网格,有一些格子是黑色的,其余是白色的,多次询问,问有几个 x×y 的子矩形。
单调栈+前缀和
对于每个格子预处理出能向左延伸的最远距离。
对于每一列单独处理。处理一列时,维护一个严格递增的单调栈,遍历每一行,当比单调栈顶短时,说明出现了极大的矩形,因为这个栈是严格递增的,所以长度等于当前长度与栈次顶长度的最大值+1,宽度等于当前行与栈次顶行之间的行数。
假设下图阴影部分是找出的一个极大子矩形。则其中包含了多个右边界与该极大子矩形相同的子矩形。
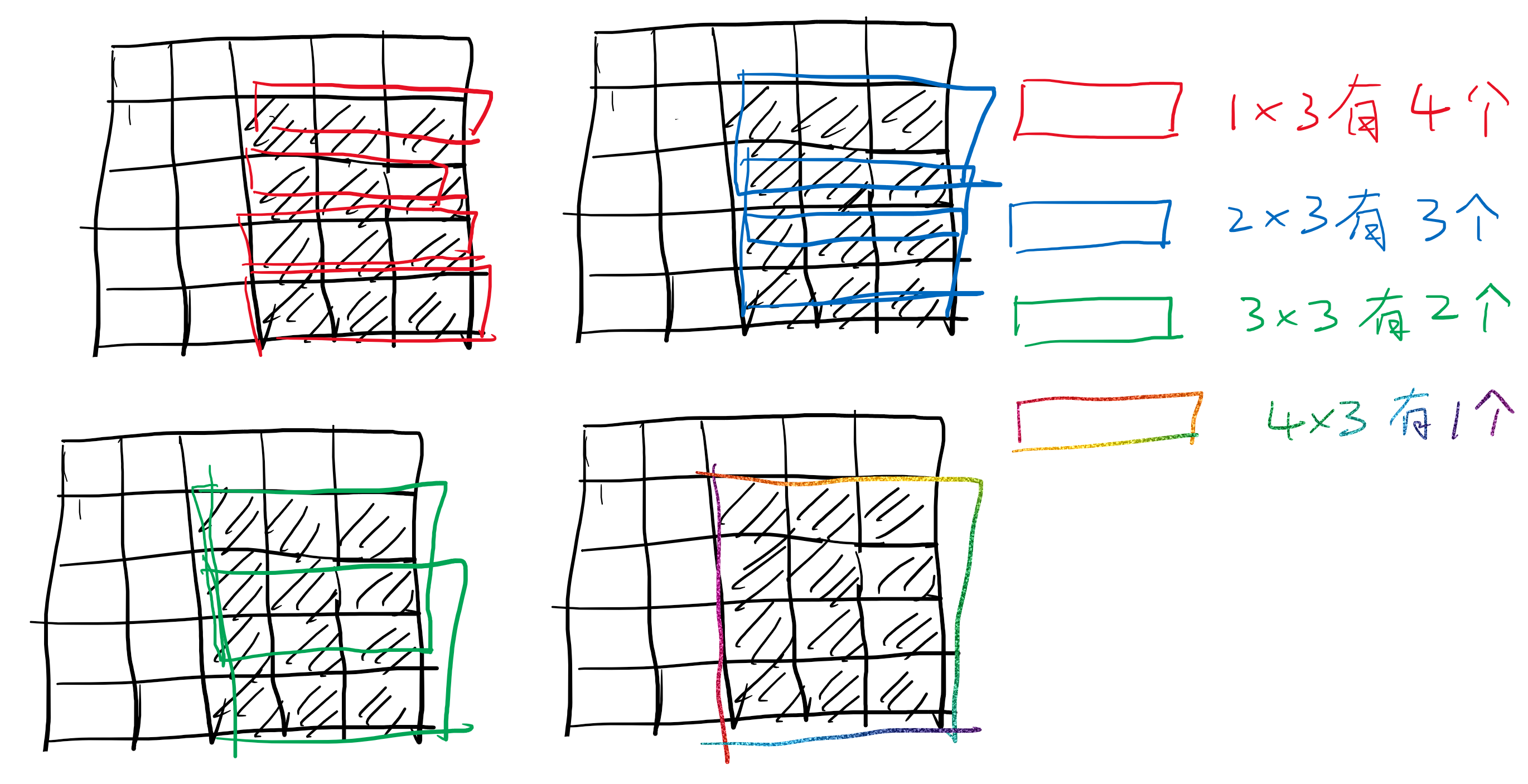
因此需要前缀和处理,可以发现上图有一个从行数为 4 到行数为 1 的递减的等差数列,这可以通过对行做两次前缀和得到。
又由于上图这些框出来的子矩形把左边界向右靠时对每一个左边界又有会有个数相同的子矩形,所以还要对列做一次前缀和。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
| #include <bits/stdc++.h>
#define debug(x) cout << #x << ":\t" << (x) << endl;
using namespace std;
#define ll long long
#define ull unsigned ll
const int N = 2e6 + 10;
const int INF = 0x3f3f3f3f;
const ll inf = 0x3f3f3f3f3f3f3f3f;
const ll mod = 1e9 + 7;
const ll inv2 = (mod + 1) / 2;
int n, m, k;
int T;
int a[2020][2020];
ll ans[2020][2020];
typedef pair<int, int>pii;
pii st[N];
int tp;
int main() {
scanf("%d%d%d", &n, &m, &k);
for (int i = 1; i <= n; i++)for (int j = 1; j <= m; j++)a[i][j] = 1;
for (int i = 1; i <= k; i++) {
int x, y;
scanf("%d%d", &x, &y);
a[x][y] = 0;
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
if (a[i][j])a[i][j] += a[i][j - 1];
}
}
for (int j = 1; j <= m; j++) {
tp = 0;
for (int i = 1; i <= n + 1; i++) {
while (tp&&st[tp].second > a[i][j]) {
pii p = st[tp];
ans[i - st[tp - 1].first - 1][max(a[i][j], st[tp - 1].second) + 1]++;
ans[i - st[tp - 1].first - 1][st[tp].second + 1]--;
tp--;
}
while (tp && st[tp].second == a[i][j])tp--;
st[++tp] = { i,a[i][j] };
}
}
for (int i = 1; i <= n; i++)for (int j = 1; j <= m; j++)ans[i][j] += ans[i][j - 1];
for (int j = 1; j <= m; j++)for (int i = n - 1; i >= 1; i--)ans[i][j] += ans[i + 1][j];
for (int j = 1; j <= m; j++)for (int i = n - 1; i >= 1; i--)ans[i][j] += ans[i + 1][j];
scanf("%d", &T);
while (T--) {
int x, y;
scanf("%d%d", &x, &y);
printf("%lld\n", ans[x][y]);
}
return 0;
}
|
F. 文艺表演
题意:n 只猫,第 i 只初始在 a[i] 处,m 次独立的询问,每次询问给定区间 [l,r] 和 K,问在要求所有编号在 [l,r] 的猫跑到位置区间 [K,K+r−l] 中,且不能在相同位置,跑动的代价为初始和最终位置的距离差的绝对值,问最小代价。
主席树
首先要猜出或者证出最优解是按照初始相对位置跑到对应位置去。保持相对顺序不变。
又要看出这样跑一定会有左边一部分猫向右跑,而右边的剩下的猫向左跑。
接下来就是主席树了。
维护两个区间,一个是旧的位置区间,一个是相对应的新的位置区间,即原先处于 [l,r] 的猫都要跑到 [s,t] 去。
若 r≤t,说明所有人都要向右跑,若 l≥s,说明所有人都要向左跑。这两种都可以直接 O(1) 求出来。注意这里并不是只有当 [l,r] 完全位于 [s,t] 左或右时才处理,而是只要 r≤t,因为既然最终所有人都会在 [s,t] 中,就说明 [l,r] 中最右侧的人要向右跑,而我们之前说过,左侧的人一定都是向右跑的,所以 [l,r] 一定都是向右跑。另一种情况也类似。
否则就要继续递归到左右儿子去,这样这样看起来复杂度不行,但是实际上只有一个儿子会达到 O(log) 的复杂度,另一个是 O(1) 的。设左儿子的两个区间是 [l,mid],[s,s+lsz−1],右儿子的两个区间是 [mid+1,r],[s+lsz,t]。假设 mid<s+lsz,则左儿子 O(1),右儿子 O(log);否则左儿子 O(1),右儿子 O(log)。
所以最终复杂度还是 O(nlogn)。关键也是在于左侧人都往右跑,右侧人都往左跑。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
| #include <bits/stdc++.h>
#define debug(x) cout << #x << ":\t" << (x) << endl;
using namespace std;
#define ll long long
#define ull unsigned ll
const int N = 2e6 + 10;
const int INF = 0x3f3f3f3f;
const ll inf = 0x3f3f3f3f3f3f3f3f;
const ll mod = 1e9 + 7;
const ll inv2 = (mod + 1) / 2;
int n, m;
int NN = 1000000;
int a[N];
int root[N], tot;
struct X
{
int l, r, cnt; ll sum;
}tr[N << 5];
#define mid ((l+r)>>1)
void upd(int q, int l, int r, int& x, int y) {
tr[++tot] = tr[y];
tr[tot].cnt++;
tr[tot].sum += q;
x = tot;
if (l == r)return;
if (q <= mid)upd(q, l, mid, tr[x].l, tr[y].l);
else upd(q, mid + 1, r, tr[x].r, tr[y].r);
}
ll qry(int l, int r, int rt1, int rt2, int s, int t) {
ll Sum = tr[rt2].sum - tr[rt1].sum;
if (r <= t) {
return 1ll*(s + t)*(t - s + 1) / 2 - Sum;
}
if (l >= s) {
return Sum - 1ll*(s + t)*(t - s + 1) / 2;
}
int lsz = tr[tr[rt2].l].cnt - tr[tr[rt1].l].cnt;
return qry(l, mid, tr[rt1].l, tr[rt2].l, s, s + lsz - 1) + qry(mid + 1, r, tr[rt1].r, tr[rt2].r, s + lsz, t);
}
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i++)scanf("%d", &a[i]);
for (int i = 1; i <= n; i++)
upd(a[i], 1, NN, root[i], root[i - 1]);
while (m--) {
int l, r, k;
scanf("%d%d%d", &l, &r, &k);
printf("%lld\n", qry(1, NN, root[l - 1], root[r], k, k + r - l));
}
return 0;
}
|







