[D. Alex and Julian][http://codeforces.com/contest/1220/problem/D]

Boy Dima gave Julian a birthday present - set BB consisting of positive integers. However, he didn’t know, that Julian hates sets, but enjoys bipartite graphs more than anything else!

Julian was almost upset, but her friend Alex said, that he can build an undirected graph using this set in such way: let all integer numbers be vertices, then connect any two ii and jj with an edge if ∣i−j∣|i−j| belongs to BB.

Unfortunately, Julian doesn’t like the graph, that was built using BB. Alex decided to rectify the situation, so he wants to erase some numbers form BB, so that graph built using the new set is bipartite. The difficulty of this task is that the graph, Alex has to work with, has an infinite number of vertices and edges! It is impossible to solve this task alone, so Alex asks you for help. Write a program that erases a subset of minimum size from BB so that graph constructed on the new set is bipartite.

Recall, that graph is bipartite if all its vertices can be divided into two disjoint sets such that every edge connects a vertex from different sets.

Input

First line contains an integer n(1⩽n⩽200000)n (1⩽n⩽200000) — size of BB

Second line contains nn integers b1,b2,…,bn(1⩽bi⩽1018)b_1,b_2,…,b_n (1⩽b_i⩽10^{18}) — numbers of BB, all bib_i are unique

Output

In first line print single integer kk – number of erased elements. In second line print kk integers – values of erased elements.

If there are multiple answers, print any of them.

Examples

input

1
2
3
1 2 3

output

1
2
1
2

input

1
2
2
2 6

output

1
0

 

题意：把所有的整数视作节点（无限多个），如果两个整数的差值在给定的B集合中，则两点连无向边，要求得到的图是二分图，求B中至少要删掉的数。

一道有趣的图论与数论结合的题目。

首先，要知道二分图等价于图上没有奇环。所以要把所有可能形成奇环的数字组合删去。

定义：设整数 m=2k1⋅am=2^{k_1}\cdot a，b=2k2⋅bb=2^{k_2}\cdot b，其中 a,ba, b 为奇数，若 k1==k2k_1==k_2，则称 m,nm,n 同阶。

以下证明，若 m，nm，n 不同阶，且 m，nm，n 都属于 BB，则必定形成奇环。

设 qq 为 m,nm,n 的最小公倍数。

我们知道，若两点之间存在两条没有重复点的路径，则会形成一个环。

那么我们取两点为 b,qb,q，其中 bb 为任意整数，qq 为上述最小公倍数。

从 bb 到 qq 构造一条路径 b−>b+m−>b+2m−>⋯−>qb->b+m->b+2m->\cdots ->q，可知这条路径上有 q/m+1q/m+1 个点。

再构造另一条路径 b−>b+n−>b+2n−>⋯−>qb->b+n->b+2n->\cdots ->q ，这条路径上有 q/n+1q/n+1 个点，则总共有 q/m+q/nq/m+q/n 个点（b，q重复计算了）。

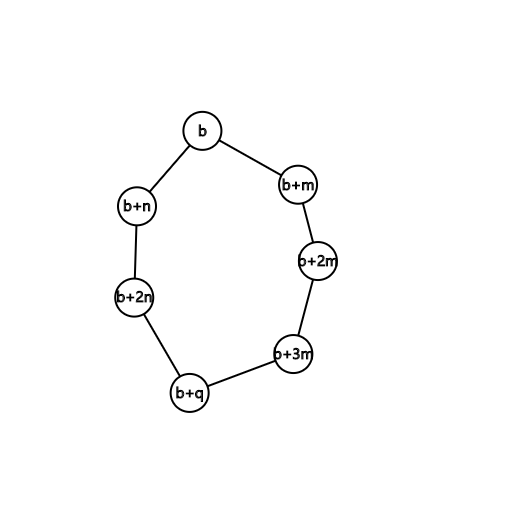
graph 1.png

由于 m,nm,n 不同阶，所以假设 m=2k⋅2p⋅am=2^k\cdot 2^p\cdot a，m=2k⋅bm=2^k\cdot b，其中 a,ba,b 为奇数。则 p=2k⋅2p⋅a⋅bp=2^k\cdot 2^p\cdot a\cdot b，则 p/mp/m，p/np/n 必定一奇一偶，和为奇数。

由于 pp 是 m,nm,n 的最小公倍数，所以两条路径上除了起点终点之外必定没有重复点。

则必定可以形成奇环。

 

以下证明，若 m,nm,n 同阶，则必定不会有奇环。

假设存在奇环，且任意一条边的两端点的差值同阶。

设 m=2k⋅a,n=2k⋅bm=2^k\cdot a,n=2^k\cdot b，其中 a,ba,b 都是奇数。

有了上一段的经验，我们可以知道，若假设环的起点为 bb ，则可以把环的边视作用 m,nm,n 进行一次加减，则奇环可以视为 bb 经过奇数次的加减后又变为了 bb ，那么这奇数次加减之和 = 0。

即

b+sum(xm,yn)=bb+sum(xm,yn)=b

sum(xm,yn)=0sum(xm,yn)=0

提出 2k2^k

2ksum(xa,yb)=02^k sum(xa,yb)=0

由于 2k!=02^k!=0

所以 sum(xa,yb)==0sum(xa,yb)==0

说明奇数个奇数的加减得到0这个偶数。与事实不符。

所以假设不成立。

结论可以类推为：有多个同阶的整数，则必定不会有奇环。

 

综上，集合中不能存在不同阶的数。

然而这么向很难实现。所以换种思路，对于任意一个数，最多可以留下与它同阶的所有数。

那么枚举阶数，同一阶数的所有数都留下，比较选哪一阶使得留下的数最多即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
#include<bits/stdc++.h>
using namespace std;
#define ll long long
typedef pair<int, int> pii;
const int maxn = 1e6 + 10;
int n;
ll a[maxn];
int id[maxn];
int cnt[maxn];
int main() {
	scanf("%d", &n);
	for (int i = 1; i <= n; i++)scanf("%I64d", &a[i]);
	for (int i = 1; i <= n; i++) {
		ll x = a[i];
		while (x && (x & 1 ^ 1)) {
			x >>= 1;
			id[i]++;
		}
		cnt[id[i]]++;
	}
	int anst = -1, ans = -1;

	for (int i = 0; i <= 64; i++) {
		if (cnt[i] > ans) {
			anst = i;
			ans = cnt[i];
		}
	}
	printf("%d\n", n - cnt[anst]);
	for (int i = 1; i <= n; i++)if (id[i] != anst)printf("%I64d ", a[i]);
	printf("\n");
	return 0;
}